problem solving involving polynomial equation calculator

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Solving Equations
• Polynomial Equation Solver

Polynomial equation solver

This calculator solves equations that are reducible to polynomial form , such as $ \color{blue}{2(x+1) + 3(x-1) = 5} $ , $ \color{blue}{(2x+1)^2 - (x-1)^2 = x} $ and $ \color{blue}{ \frac{2x+1}{2} + \frac{3-4x}{3} = 1} $ . The calculator will try to find an exact solution; if this is not possible, it will use the cubic or quartic formulas.

The calculator will also walk you through each step and give you a detailed explanation on how to simplify and solve the equation.

• Factoring Polynomials
• Solving equations
• Rationalize Denominator
• Arithmetic sequences
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance and Midpoint
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Related Calculators

Was this calculator helpful?

Please tell me how can I make this better.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Polynomial Equations

Instructions: Use calculator to solve a polynomial equation that you provide, showing all the steps. Please type the polynomial equation you want to solve in the form below .

About Polynomial Equations

Use this calculator to help you solve polynomial equations, showing all the steps of the process. The equation you provide can have polynomial terms on the left and right of the equation.

For example, you can provide an equation like 3x^3 - 2x = 1 + x, which could be derived from trying to find the intersection of the graphs of a cubic and a linear function. Any polynomial equation will do, with integer or fraction coefficients, or any valid numeric expression.

Once a polynomial equation is typed into the form box, you need to click on "Calculate", that will show all the steps of the process and solutions.

One disclaimer, not all polynomial equations can be solved with basic tools. There is no systematic formula to deal with polynomial equation of degree 5 or higher. Also, we deal with the added difficulty that the solutions to a polynomial equation can be complex numbers.

What is a polynomial Equation

A polynomial equation, in simple terms, is an equation in which both sides contain polynomials. Mathematically, a polynomial equation is of the form:

where \(p(x)\) and \(q(x)\) are polynomials. For example \(3x+1 = x^2-2\) is a polynomial equation, but \(\sin(3x+1) = x^2-2\) is not.

What are the steps for Solving Polynomial Equations?

• Step 1: Identify the equation you want to work with, indicating clearly the terms on the left and right side, and make sure they are polynomials
• Step 2: Simplify each side as much as possible. Pass all the terms on one of the sides to the other (if both sides have terms)
• Step 3: Now you have a polynomial equation that is set to be equal to zero, so we need to find the roots of the polynomial
• Step 4: We try with possible rational roots, polynomial division for reduction and quadratic formula, as shown in the polynomial zero calculator to find the solutions, if possible

You will find that solving polynomial equations, as finding roots of a polynomial is far from trivial for all cases. Surely, some specific examples can be very simple, but when the exponent of the polynomials involved is large, the process can be very difficult or simply impossible.

Are Quadratic Equations also Polynomial Equations?

Yes indeed! A quadratic equation is an equation with a polynomial of degree 2 on the left side, and 0 (which is a polynomial too) on the right side, so it fits on the definition.

Indeed, quadratic equations are about the best we can solve with simple tools. Though there are formulas for cubic and quartic equations, there is no general formula for degree 5 or higher. So then we rely on computers to find numerical approximations often times.

Also, not only the exponent of the polynomial can make an equation hard to solve, also cumbersome polynomial coefficients can certainly make things more difficult.

How are graph of polynomials related to polynomial equations?

There are different ways of seeing it, but one way is to notice that by trying to find the intersection of different polynomials, we are indeed solving a polynomial equation. So there are tightly related problems.

Example: Solving polynomial equations

Calculate the following polynomial equation: \(x^2 = x^3\)

Solution: We have to solve \(x^2 = x^3\), so we pass \(x^3\) to the other side, so we get

and factoring leads to:

So then there are two solutions: \(x_1 = 0\) (which has multiplicity 2), and \(x_2 = 1\).

Example: Solving polynomial Equations

What are the solutions of the following equation: \(\frac{2}{3} x^2 + \frac{5}{4} x = \frac{1}{3} x^2 - \frac{5}{6}\)

Solution: We need to solve the following equation:

Initial Step: In this case, we first need to simplify the given equation \(\displaystyle \frac{2}{3}x^2+\frac{5}{4}x=\frac{1}{3}x^2-\frac{5}{6} \), by putting all the terms on one side of the equation, so we get:

Hence, after simplifying, we need to solve the following polynomial equation of order \(2\):

Observe that the degree of the given polynomial is \(\displaystyle deg(p) = 2\), its leading coefficient is \(\displaystyle a_{2} = \frac{1}{3}\) and its constant coefficient is \(\displaystyle a_0 = \frac{5}{6}\).

We need to solve the following given quadratic equation \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6}=0\).

For a quadratic equation of the form \(a x^2 + bx + c = 0\), the roots are computed using the following formula:

In this case, we have that the equation we need to solve is \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = 0\), which implies that corresponding coefficients are:

First, we will compute the discriminant to assess the nature of the roots. The discriminating is computed as:

Since in this case we get the discriminant is \(\Delta = \displaystyle \frac{65}{144} > 0\), which is positive, we know that the equation has two different real roots.

Now, plugging these values into the formula for the roots we get:

so then, we find that:

In this case, the quadratic equation \( \displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = 0 \), has two real roots, so then:

so then the original polynomial is factored as \(\displaystyle p(x) = \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = \frac{1}{3} \left(x+\frac{1}{8}\sqrt{65}+\frac{15}{8}\right)\left(x-\frac{1}{8}\sqrt{65}+\frac{15}{8}\right) \), which completes the factorization.

Conclusion : The solution to the polynomial equation found using the factorization process are \(-\frac{1}{8}\sqrt{65}-\frac{15}{8}\) and \(\frac{1}{8}\sqrt{65}-\frac{15}{8}\) .

More polynomial calculators

Polynomials equations appear so naturally in Algebra, that they are one of the most important topics in Algebra. When you are looking for the intersection of two parabolas , you will need to solve a polynomial equation , just to mention one situation of many.

The simplest case of a polynomial equation is the case when you solve a linear equation , which is indeed a trivial case. Anything that is not linear will take a whole lot of more work.

Solving polynomial equation is not straightforward, especially for higher polynomial degrees . Indeed, there is as certain possibility that you won't be able to find all the solution of a given equation manually (or any solution for that matter).

The best manual alternative involves grouping all the polynomial terms on one side to reduce it to finding the zeros of a polynomial . Then, we use the quadratic formula when possible, and try to reduce the order of the polynomial by polynomial division and the factor theorem .

Other Calculators

log in to your account

Reset password.

• calculators
• Polynomials

Polynomials Calculator

Get detailed solutions to your math problems with our polynomials step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems.

Solved example of polynomials

Multiply the single term $2x+3$ by each term of the polynomial $\left(6x-5\right)$

Multiply the single term $6x$ by each term of the polynomial $\left(2x+3\right)$

When multiplying two powers that have the same base ($x$), you can add the exponents

Multiply the single term $-5$ by each term of the polynomial $\left(2x+3\right)$

Combining like terms $18x$ and $-10x$

 Final Answer

Struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Related Calculators

 popular problems.

Related Content

• Synthetic Division
• Relative Extrema Calculator
• Riemann Sum Calculator
• Inflection Point Calculator
• Euler’s Method Calculator
• Tangent Plane Calculator
• Implicit Differentiation Calculator

On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!

Nikkolas and Alex Founders and Owners of Voovers

Polynomial Calculator

Lesson on Solving Polynomials

Lesson contents, how to solve for a polynomial variable.

When solving for a variable within a polynomial equation, we work algebraically to isolate it. To isolate a variable, we use the reverse order of operations to move all terms and numbers to the opposite side of the equation of the variable. Once the target variable is alone on one side of the equation, it is solved.

Solving Variables in Special Polynomials

Some polynomial equation variables cannot be solved via basic isolation techniques. For these special polynomials, we may use a variety of other solving techniques.

Commonly used techniques are factoring and the quadratic formula. Factoring may be used when the variable has an exponent. The quadratic formula may be used for second-degree polynomials.

Sometimes a polynomial does not have any real, whole number, fractional, or rational solutions. When this happens, we may employ a computer that solves using numerical computation. The calculator on this page uses numerical computation for these special case polynomials.

How to Factor Polynomials

Factoring a polynomial is effectively the reverse action of simplifying terms grouped by parenthesis. For any factorable polynomial, we may use a method called completing the square (see our lesson for full tutorial). A polynomial must be in an equation to complete the square.

If we are simply factoring a polynomial for the sake of reaching factored form, we are finished once the square is completed. However, completing the square also enables us to determine the zeroes or “roots” of an equation by converting it to a factored form if we desire a solution to a variable.

How the Calculator Works

This calculator is written entirely in the programming language JavaScript (JS) and utilizes a JS-native computer algebra system (CAS). Because your device’s internet browser has a built-in JS engine, this calculator runs instantly when the calculate button is pressed. Therefore, a solution is available immediately and without the page needing to reload with data from the server.

The CAS is fed your polynomial and whether you are solving for x or factoring. The CAS treats the computation symbolically, preserving exact values of variables and numbers. In special cases where there are no rational or real number solutions, the CAS uses numerical methods to achieve a very accurate, approximated solution.

Once your answer is calculated, it is converted to LaTeX code. LaTeX is a math markup and rendering language that allows for graphical equation printing on webpages. This page’s local LaTeX script renders that code in the answer area as the solution you see.

Insert/edit link

Enter the destination URL

Or link to existing content

6.5 Polynomial Equations

Learning objectives.

By the end of this section, you will be able to:

Use the Zero Product Property

• Solve quadratic equations by factoring
• Solve equations with polynomial functions
• Solve applications modeled by polynomial equations

Be Prepared 6.10

Before you get started, take this readiness quiz.

Solve: 5 y − 3 = 0 . 5 y − 3 = 0 . If you missed this problem, review Example 2.2 .

Be Prepared 6.11

Factor completely: n 3 − 9 n 2 − 22 n . n 3 − 9 n 2 − 22 n . If you missed this problem, review Example 3.48 .

Be Prepared 6.12

If f ( x ) = 8 x − 16 , f ( x ) = 8 x − 16 , find f ( 3 ) f ( 3 ) and solve f ( x ) = 0 . f ( x ) = 0 . If you missed this problem, review Example 3.59 .

We have spent considerable time learning how to factor polynomials. We will now look at polynomial equations and solve them using factoring, if possible.

A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.

Polynomial Equation

A polynomial equation is an equation that contains a polynomial expression.

The degree of the polynomial equation is the degree of the polynomial.

We have already solved polynomial equations of degree one . Polynomial equations of degree one are linear equations are of the form a x + b = c . a x + b = c .

We are now going to solve polynomial equations of degree two . A polynomial equation of degree two is called a quadratic equation . Listed below are some examples of quadratic equations:

The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get n 2 + n . n 2 + n .

The general form of a quadratic equation is a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , with a ≠ 0 . a ≠ 0 . (If a = 0 , a = 0 , then 0 · x 2 = 0 0 · x 2 = 0 and we are left with no quadratic term.)

Quadratic Equation

An equation of the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 is called a quadratic equation.

To solve quadratic equations we need methods different from the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.

We will first solve some quadratic equations by using the Zero Product Property . The Zero Product Property says that if the product of two quantities is zero, then at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.

Zero Product Property

If a · b = 0 , a · b = 0 , then either a = 0 a = 0 or b = 0 b = 0 or both.

We will now use the Zero Product Property, to solve a quadratic equation .

Example 6.44

How to solve a quadratic equation using the zero product property.

Solve: ( 5 n − 2 ) ( 6 n − 1 ) = 0 . ( 5 n − 2 ) ( 6 n − 1 ) = 0 .

Try It 6.87

Solve: ( 3 m − 2 ) ( 2 m + 1 ) = 0 . ( 3 m − 2 ) ( 2 m + 1 ) = 0 .

Try It 6.88

Solve: ( 4 p + 3 ) ( 4 p − 3 ) = 0 . ( 4 p + 3 ) ( 4 p − 3 ) = 0 .

Use the Zero Product Property.

• Step 1. Set each factor equal to zero.
• Step 2. Solve the linear equations.
• Step 3. Check.

Solve Quadratic Equations by Factoring

The Zero Product Property works very nicely to solve quadratic equations. The quadratic equation must be factored, with zero isolated on one side. So we must be sure to start with the quadratic equation in standard form , a x 2 + b x + c = 0 . a x 2 + b x + c = 0 . Then we must factor the expression on the left.

Example 6.45

How to solve a quadratic equation by factoring.

Solve: 2 y 2 = 13 y + 45 . 2 y 2 = 13 y + 45 .

Try It 6.89

Solve: 3 c 2 = 10 c − 8 . 3 c 2 = 10 c − 8 .

Try It 6.90

Solve: 2 d 2 − 5 d = 3 . 2 d 2 − 5 d = 3 .

Solve a quadratic equation by factoring.

• Step 1. Write the quadratic equation in standard form, a x 2 + b x + c = 0 . a x 2 + b x + c = 0 .
• Step 2. Factor the quadratic expression.
• Step 3. Use the Zero Product Property.
• Step 4. Solve the linear equations.
• Step 5. Check. Substitute each solution separately into the original equation.

Before we factor, we must make sure the quadratic equation is in standard form .

Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in this chapter! Do you recognize the special product pattern in the next example?

Example 6.46

Solve: 169 x 2 = 49 . 169 x 2 = 49 .

We leave the check up to you.

Try It 6.91

Solve: 25 p 2 = 49 . 25 p 2 = 49 .

Try It 6.92

Solve: 36 x 2 = 121 . 36 x 2 = 121 .

In the next example, the left side of the equation is factored, but the right side is not zero. In order to use the Zero Product Property , one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.

Example 6.47

Solve: ( 3 x − 8 ) ( x − 1 ) = 3 x . ( 3 x − 8 ) ( x − 1 ) = 3 x .

Try It 6.93

Solve: ( 2 m + 1 ) ( m + 3 ) = 1 2 m . ( 2 m + 1 ) ( m + 3 ) = 1 2 m .

Try It 6.94

Solve: ( k + 1 ) ( k − 1 ) = 8 . ( k + 1 ) ( k − 1 ) = 8 .

In the next example, when we factor the quadratic equation we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.

Example 6.48

Solve: 3 x 2 = 12 x + 63 . 3 x 2 = 12 x + 63 .

Try It 6.95

Solve: 18 a 2 − 30 = −33 a . 18 a 2 − 30 = −33 a .

Try It 6.96

Solve: 123 b = −6 − 60 b 2 . 123 b = −6 − 60 b 2 .

The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree greater than two by using the Zero Product Property, just like we solved quadratic equations.

Example 6.49

Solve: 9 m 3 + 100 m = 60 m 2 . 9 m 3 + 100 m = 60 m 2 .

Try It 6.97

Solve: 8 x 3 = 24 x 2 − 18 x . 8 x 3 = 24 x 2 − 18 x .

Try It 6.98

Solve: 16 y 2 = 32 y 3 + 2 y . 16 y 2 = 32 y 3 + 2 y .

Solve Equations with Polynomial Functions

As our study of polynomial functions continues, it will often be important to know when the function will have a certain value or what points lie on the graph of the function. Our work with the Zero Product Property will be help us find these answers.

Example 6.50

For the function f ( x ) = x 2 + 2 x − 2 , f ( x ) = x 2 + 2 x − 2 ,

ⓐ find x when f ( x ) = 6 f ( x ) = 6 ⓑ find two points that lie on the graph of the function.

ⓑ Since f ( −4 ) = 6 f ( −4 ) = 6 and f ( 2 ) = 6 , f ( 2 ) = 6 , the points ( −4 , 6 ) ( −4 , 6 ) and ( 2 , 6 ) ( 2 , 6 ) lie on the graph of the function.

Try It 6.99

For the function f ( x ) = x 2 − 2 x − 8 , f ( x ) = x 2 − 2 x − 8 ,

ⓐ find x when f ( x ) = 7 f ( x ) = 7 ⓑ Find two points that lie on the graph of the function.

Try It 6.100

For the function f ( x ) = x 2 − 8 x + 3 , f ( x ) = x 2 − 8 x + 3 ,

ⓐ find x when f ( x ) = −4 f ( x ) = −4 ⓑ Find two points that lie on the graph of the function.

The Zero Product Property also helps us determine where the function is zero. A value of x where the function is 0, is called a zero of the function .

Zero of a Function

For any function f , if f ( x ) = 0 , f ( x ) = 0 , then x is a zero of the function .

When f ( x ) = 0 , f ( x ) = 0 , the point ( x , 0 ) ( x , 0 ) is a point on the graph. This point is an x -intercept of the graph. It is often important to know where the graph of a function crosses the axes. We will see some examples later.

Example 6.51

For the function f ( x ) = 3 x 2 + 10 x − 8 , f ( x ) = 3 x 2 + 10 x − 8 , find

ⓐ the zeros of the function, ⓑ any x -intercepts of the graph of the function, ⓒ any y -intercepts of the graph of the function

ⓐ To find the zeros of the function, we need to find when the function value is 0.

ⓑ An x -intercept occurs when y = 0 . y = 0 . Since f ( −4 ) = 0 f ( −4 ) = 0 and f ( 2 3 ) = 0 , f ( 2 3 ) = 0 , the points ( −4 , 0 ) ( −4 , 0 ) and ( 2 3 , 0 ) ( 2 3 , 0 ) lie on the graph. These points are x -intercepts of the function. ⓒ A y -intercept occurs when x = 0 . x = 0 . To find the y -intercepts we need to find f ( 0 ) . f ( 0 ) .

Since f ( 0 ) = −8 , f ( 0 ) = −8 , the point ( 0 , −8 ) ( 0 , −8 ) lies on the graph. This point is the y -intercept of the function.

Try It 6.101

For the function f ( x ) = 2 x 2 − 7 x + 5 , f ( x ) = 2 x 2 − 7 x + 5 , find

ⓐ the zeros of the function, ⓑ any x -intercepts of the graph of the function, ⓒ any y -intercepts of the graph of the function.

Try It 6.102

For the function f ( x ) = 6 x 2 + 13 x − 15 , f ( x ) = 6 x 2 + 13 x − 15 , find

Solve Applications Modeled by Polynomial Equations

The problem-solving strategy we used earlier for applications that translate to linear equations will work just as well for applications that translate to polynomial equations. We will copy the problem-solving strategy here so we can use it for reference.

Use a problem solving strategy to solve word problems.

• Step 1. Read the problem. Make sure all the words and ideas are understood.
• Step 2. Identify what we are looking for.
• Step 3. Name what we are looking for. Choose a variable to represent that quantity.
• Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Step 5. Solve the equation using appropriate algebra techniques.
• Step 6. Check the answer in the problem and make sure it makes sense.
• Step 7. Answer the question with a complete sentence.

We will start with a number problem to get practice translating words into a polynomial equation.

Example 6.52

The product of two consecutive odd integers is 323. Find the integers.

Try It 6.103

The product of two consecutive odd integers is 255. Find the integers.

Try It 6.104

The product of two consecutive odd integers is 483 Find the integers.

Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give positive results.

In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.

Example 6.53

A rectangular bedroom has an area 117 square feet. The length of the bedroom is four feet more than the width. Find the length and width of the bedroom.

Try It 6.105

A rectangular sign has an area of 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.

Try It 6.106

A rectangular patio has an area of 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

In the next example, we will use the Pythagorean Theorem ( a 2 + b 2 = c 2 ) . ( a 2 + b 2 = c 2 ) . This formula gives the relation between the legs and the hypotenuse of a right triangle.

We will use this formula to in the next example.

Example 6.54

A boat’s sail is in the shape of a right triangle as shown. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the sail.

Try It 6.107

Justine wants to put a deck in the corner of her backyard in the shape of a right triangle. The length of one side of the deck is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the deck.

Try It 6.108

A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of the other leg. Find the lengths of the hypotenuse and the other leg.

The next example uses the function that gives the height of an object as a function of time when it is thrown from 80 feet above the ground.

Example 6.55

Dennis is going to throw his rubber band ball upward from the top of a campus building. When he throws the rubber band ball from 80 feet above the ground, the function h ( t ) = −16 t 2 + 64 t + 80 h ( t ) = −16 t 2 + 64 t + 80 models the height, h , of the ball above the ground as a function of time, t. Find:

ⓐ the zeros of this function which tell us when the ball hits the ground, ⓑ when the ball will be 80 feet above the ground, ⓒ the height of the ball at t = 2 t = 2 seconds.

ⓐ The zeros of this function are found by solving h ( t ) = 0 . h ( t ) = 0 . This will tell us when the ball will hit the ground.

The result t = 5 t = 5 tells us the ball will hit the ground 5 seconds after it is thrown. Since time cannot be negative, the result t = −1 t = −1 is discarded.

ⓑ The ball will be 80 feet above the ground when h ( t ) = 80 . h ( t ) = 80 .

ⓒ To find the height ball at t = 2 t = 2 seconds we find h ( 2 ) . h ( 2 ) .

Try It 6.109

Genevieve is going to throw a rock from the top a trail overlooking the ocean. When she throws the rock upward from 160 feet above the ocean, the function h ( t ) = −16 t 2 + 48 t + 160 h ( t ) = −16 t 2 + 48 t + 160 models the height, h , of the rock above the ocean as a function of time, t . Find:

ⓐ the zeros of this function which tell us when the rock will hit the ocean, ⓑ when the rock will be 160 feet above the ocean, ⓒ the height of the rock at t = 1.5 t = 1.5 seconds.

Try It 6.110

Calib is going to throw his lucky penny from his balcony on a cruise ship. When he throws the penny upward from 128 feet above the ground, the function h ( t ) = −16 t 2 + 32 t + 128 h ( t ) = −16 t 2 + 32 t + 128 models the height, h , of the penny above the ocean as a function of time, t . Find:

ⓐ the zeros of this function which is when the penny will hit the ocean, ⓑ when the penny will be 128 feet above the ocean, ⓒ the height the penny will be at t = 1 t = 1 seconds which is when the penny will be at its highest point.

Access this online resource for additional instruction and practice with quadratic equations.

• Beginning Algebra & Solving Quadratics with the Zero Property

Section 6.5 Exercises

Practice makes perfect.

In the following exercises, solve.

( 3 a − 10 ) ( 2 a − 7 ) = 0 ( 3 a − 10 ) ( 2 a − 7 ) = 0

( 5 b + 1 ) ( 6 b + 1 ) = 0 ( 5 b + 1 ) ( 6 b + 1 ) = 0

6 m ( 12 m − 5 ) = 0 6 m ( 12 m − 5 ) = 0

2 x ( 6 x − 3 ) = 0 2 x ( 6 x − 3 ) = 0

( 2 x − 1 ) 2 = 0 ( 2 x − 1 ) 2 = 0

( 3 y + 5 ) 2 = 0 ( 3 y + 5 ) 2 = 0

5 a 2 − 26 a = 24 5 a 2 − 26 a = 24

4 b 2 + 7 b = −3 4 b 2 + 7 b = −3

4 m 2 = 17 m − 15 4 m 2 = 17 m − 15

n 2 = 5 n − 6 n 2 = 5 n − 6

7 a 2 + 14 a = 7 a 7 a 2 + 14 a = 7 a

12 b 2 − 15 b = −9 b 12 b 2 − 15 b = −9 b

49 m 2 = 144 49 m 2 = 144

625 = x 2 625 = x 2

16 y 2 = 81 16 y 2 = 81

64 p 2 = 225 64 p 2 = 225

121 n 2 = 36 121 n 2 = 36

100 y 2 = 9 100 y 2 = 9

( x + 6 ) ( x − 3 ) = −8 ( x + 6 ) ( x − 3 ) = −8

( p − 5 ) ( p + 3 ) = −7 ( p − 5 ) ( p + 3 ) = −7

( 2 x + 1 ) ( x − 3 ) = −4 x ( 2 x + 1 ) ( x − 3 ) = −4 x

( y − 3 ) ( y + 2 ) = 4 y ( y − 3 ) ( y + 2 ) = 4 y

( 3 x − 2 ) ( x + 4 ) = 12 x ( 3 x − 2 ) ( x + 4 ) = 12 x

( 2 y − 3 ) ( 3 y − 1 ) = 8 y ( 2 y − 3 ) ( 3 y − 1 ) = 8 y

20 x 2 − 60 x = −45 20 x 2 − 60 x = −45

3 y 2 − 18 y = −27 3 y 2 − 18 y = −27

15 x 2 − 10 x = 40 15 x 2 − 10 x = 40

14 y 2 − 77 y = −35 14 y 2 − 77 y = −35

18 x 2 − 9 = −21 x 18 x 2 − 9 = −21 x

16 y 2 + 12 = −32 y 16 y 2 + 12 = −32 y

16 p 3 = 24 p 2 – 9 p 16 p 3 = 24 p 2 – 9 p

m 3 − 2 m 2 = − m m 3 − 2 m 2 = − m

2 x 3 + 72 x = 24 x 2 2 x 3 + 72 x = 24 x 2

3 y 3 + 48 y = 24 y 2 3 y 3 + 48 y = 24 y 2

36 x 3 + 24 x 2 = −4 x 36 x 3 + 24 x 2 = −4 x

2 y 3 + 2 y 2 = 12 y 2 y 3 + 2 y 2 = 12 y

For the function, f ( x ) = x 2 − 8 x + 8 , f ( x ) = x 2 − 8 x + 8 , ⓐ find when f ( x ) = −4 f ( x ) = −4 ⓑ Use this information to find two points that lie on the graph of the function.

For the function, f ( x ) = x 2 + 11 x + 20 , f ( x ) = x 2 + 11 x + 20 , ⓐ find when f ( x ) = −8 f ( x ) = −8 ⓑ Use this information to find two points that lie on the graph of the function.

For the function, f ( x ) = 8 x 2 − 18 x + 5 , f ( x ) = 8 x 2 − 18 x + 5 , ⓐ find when f ( x ) = −4 f ( x ) = −4 ⓑ Use this information to find two points that lie on the graph of the function.

For the function, f ( x ) = 18 x 2 + 15 x − 10 , f ( x ) = 18 x 2 + 15 x − 10 , ⓐ find when f ( x ) = 15 f ( x ) = 15 ⓑ Use this information to find two points that lie on the graph of the function.

In the following exercises, for each function, find: ⓐ the zeros of the function ⓑ the x -intercepts of the graph of the function ⓒ the y -intercept of the graph of the function.

f ( x ) = 9 x 2 − 4 f ( x ) = 9 x 2 − 4

f ( x ) = 25 x 2 − 49 f ( x ) = 25 x 2 − 49

f ( x ) = 6 x 2 − 7 x − 5 f ( x ) = 6 x 2 − 7 x − 5

f ( x ) = 12 x 2 − 11 x + 2 f ( x ) = 12 x 2 − 11 x + 2

Solve Applications Modeled by Quadratic Equations

The product of two consecutive odd integers is 143. Find the integers.

The product of two consecutive odd integers is 195. Find the integers.

The product of two consecutive even integers is 168. Find the integers.

The product of two consecutive even integers is 288. Find the integers.

The area of a rectangular carpet is 28 square feet. The length is three feet more than the width. Find the length and the width of the carpet.

A rectangular retaining wall has area 15 square feet. The height of the wall is two feet less than its length. Find the height and the length of the wall.

The area of a bulletin board is 55 square feet. The length is four feet less than three times the width. Find the length and the width of the a bulletin board.

A rectangular carport has area 150 square feet. The width of the carport is five feet less than twice its length. Find the width and the length of the carport.

A pennant is shaped like a right triangle, with hypotenuse 10 feet. The length of one side of the pennant is two feet longer than the length of the other side. Find the length of the two sides of the pennant.

A stained glass window is shaped like a right triangle. The hypotenuse is 15 feet. One leg is three more than the other. Find the lengths of the legs.

A reflecting pool is shaped like a right triangle, with one leg along the wall of a building. The hypotenuse is 9 feet longer than the side along the building. The third side is 7 feet longer than the side along the building. Find the lengths of all three sides of the reflecting pool.

A goat enclosure is in the shape of a right triangle. One leg of the enclosure is built against the side of the barn. The other leg is 4 feet more than the leg against the barn. The hypotenuse is 8 feet more than the leg along the barn. Find the three sides of the goat enclosure.

Juli is going to launch a model rocket in her back yard. When she launches the rocket, the function h ( t ) = −16 t 2 + 32 t h ( t ) = −16 t 2 + 32 t models the height, h , of the rocket above the ground as a function of time, t . Find:

ⓐ the zeros of this function, which tell us when the rocket will be on the ground. ⓑ the time the rocket will be 16 feet above the ground.

Gianna is going to throw a ball from the top floor of her middle school. When she throws the ball from 48 feet above the ground, the function h ( t ) = −16 t 2 + 32 t + 48 h ( t ) = −16 t 2 + 32 t + 48 models the height, h , of the ball above the ground as a function of time, t . Find:

ⓐ the zeros of this function which tells us when the ball will hit the ground. ⓑ the time(s) the ball will be 48 feet above the ground. ⓒ the height the ball will be at t = 1 t = 1 seconds which is when the ball will be at its highest point.

Writing Exercises

Explain how you solve a quadratic equation. How many answers do you expect to get for a quadratic equation?

Give an example of a quadratic equation that has a GCF and none of the solutions to the equation is zero.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/6-5-polynomial-equations

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Game Central

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Solving Polynomial Equations

• Last updated
• Save as PDF
• Page ID 134534

Learning Objectives

By the end of this section, you will be able to:

Use the Zero Product Property

• Solve quadratic equations by factoring
• Solve equations with polynomial functions
• Solve applications modeled by polynomial equations

Before you get started, take this readiness quiz.

• Solve: \(5y−3=0\). If you missed this problem, review [link] .
• Factor completely: \(n^3−9n^2−22n\). If you missed this problem, review [link] .
• If \(f(x)=8x−16\), find \(f(3)\) and solve \(f(x)=0\). If you missed this problem, review [link] .

We have spent considerable time learning how to factor polynomials. We will now look at polynomial equations and solve them using factoring, if possible.

A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.

POLYNOMIAL EQUATION

A polynomial equation is an equation that contains a polynomial expression.

The degree of the polynomial equation is the degree of the polynomial.

We have already solved polynomial equations of degree one . Polynomial equations of degree one are linear equations are of the form \(ax+b=c\).

We are now going to solve polynomial equations of degree two . A polynomial equation of degree two is called a quadratic equation . Listed below are some examples of quadratic equations:

\[x^2+5x+6=0 \qquad 3y^2+4y=10 \qquad 64u^2−81=0 \qquad n(n+1)=42 \nonumber\]

The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get \(n^2+n\).

The general form of a quadratic equation is \(ax^2+bx+c=0\), with \(a\neq 0\). (If \(a=0\), then \(0·x^2=0\) and we are left with no quadratic term.)

QUADRATIC EQUATION

An equation of the form \(ax^2+bx+c=0\) is called a quadratic equation.

\[a,b,\text{ and }c\text{ are real numbers and }a\neq 0\nonumber\]

To solve quadratic equations we need methods different from the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.

We will first solve some quadratic equations by using the Zero Product Property . The Zero Product Property says that if the product of two quantities is zero, then at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.

ZERO PRODUCT PROPERTY

If \(a·b=0\), then either \(a=0\) or \(b=0\) or both.

We will now use the Zero Product Property, to solve a quadratic equation .

Example \(\PageIndex{1}\): How to Solve a Quadratic Equation Using the Zero Product Property

Solve: \((5n−2)(6n−1)=0\).

Example \(\PageIndex{2}\)

Solve: \((3m−2)(2m+1)=0\).

\(m=\frac{2}{3},\space m=−\frac{1}{2}\)

Example \(\PageIndex{3}\)

Solve: \((4p+3)(4p−3)=0\).

\(p=−\frac{3}{4},\space p=\frac{3}{4}\)

USE THE ZERO PRODUCT PROPERTY.

• Set each factor equal to zero.
• Solve the linear equations.

Solve Quadratic Equations by Factoring

The Zero Product Property works very nicely to solve quadratic equations. The quadratic equation must be factored, with zero isolated on one side. So we be sure to start with the quadratic equation in standard form , \(ax^2+bx+c=0\). Then we factor the expression on the left.

Solve: \(2y^2=13y+45\).

Example \(\PageIndex{5}\)

Solve: \(3c^2=10c−8\).

\(c=2,\space c=\frac{4}{3}\)

Example \(\PageIndex{6}\)

Solve: \(2d^2−5d=3\).

\(d=3,\space d=−12\)

SOLVE A QUADRATIC EQUATION BY FACTORING.

• Write the quadratic equation in standard form, \(ax^2+bx+c=0\).
• Factor the quadratic expression.
• Use the Zero Product Property.
• Check. Substitute each solution separately into the original equation.

Before we factor, we must make sure the quadratic equation is in standard form .

Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in this chapter! Do you recognize the special product pattern in the next example?

Example \(\PageIndex{7}\)

Solve: \(169q^2=49\).

\(\begin{array} {ll} &169x^2=49 \\ \text{Write the quadratic equation in standard form.} &169x^2−49=0 \\ \text{Factor. It is a difference of squares.} &(13x−7)(13x+7)=0 \\ \text{Use the Zero Product Property to set each factor to }0. & \\ \text{Solve each equation.} &\begin{array} {ll} 13x−7=0 &13x+7=0 \\ 13x=7 &13x=−7 \\ x=\frac{7}{13} &x=−\frac{7}{13} \end{array} \end{array}\)

We leave the check up to you.

Example \(\PageIndex{8}\)

Solve: \(25p^2=49\).

\(p=\frac{7}{5},p=−\frac{7}{5}\)

Example \(\PageIndex{9}\)

Solve: \(36x^2=121\).

\(x=\frac{11}{6},x=−\frac{11}{6}\)

In the next example, the left side of the equation is factored, but the right side is not zero. In order to use the Zero Product Property , one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.

Example \(\PageIndex{10}\)

Solve: \((3x−8)(x−1)=3x\).

\(\begin{array} {ll} &(3x−8)(x−1)=3x \\ \text{Multiply the binomials.} &3x^2−11x+8=3x \\ \text{Write the quadratic equation in standard form.} &3x^2−14x+8=0 \\ \text{Factor the trinomial.} &(3x−2)(x−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {ll} 3x−2=0 &x−4=0 \\ 3x=2 &x=4 \\ x=\frac{2}{3} & \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)

Example \(\PageIndex{11}\)

Solve: \((2m+1)(m+3)=12m\).

\(m=1,\space m=\frac{3}{2}\)

Example \(\PageIndex{12}\)

Solve: \((k+1)(k−1)=8\).

\(k=3,\space k=−3\)

In the next example, when we factor the quadratic equation we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.

Example \(\PageIndex{13}\)

Solve: \(3x^2=12x+63\).

\(\begin{array} {ll} &3x^2=12x+63 \\ \text{Write the quadratic equation in standard form.} &3x^2−12x−63=0 \\ \text{Factor the greatest common factor first.} &3(x^2−4x−21)=0 \\ \text{Factor the trinomial.} &3(x−7)(x+3)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {lll} 3\neq 0 &x−7=0 &x+3=0 \\ 3\neq 0 &x=7 &x=−3 \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)

Example \(\PageIndex{14}\)

Solve: \(18a^2−30=−33a\).

\(a=−\frac{5}{2},a=\frac{2}{3}\)

Example \(\PageIndex{15}\)

Solve: \(123b=−6−60b^2\)

\(b=−2,\space b=−\frac{1}{20}\)

The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree greater than two by using the Zero Product Property, just like we solved quadratic equations.

Example \(\PageIndex{16}\)

Solve: \(9m^3+100m=60m^2\)

\(\begin{array} {ll} & 9m^3+100m=60m^2 \\ \text{Bring all the terms to one side so that the other side is zero.} &9m^3−60m^2+100m=0 \\ \text{Factor the greatest common factor first.} &m(9m^2−60m+100)=0 \\ \text{Factor the trinomial.} &m(3m−10)^2=0 \end{array}\\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} &\begin{array} {lll} m=0 &3m−10=0 &{}\\ m=0 &m=\frac{10}{3} & {} \end{array}\\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)

Example \(\PageIndex{17}\)

Solve: \(8x^3=24x^2−18x\).

\(x=0,\space x=\frac{3}{2}\)

Example \(\PageIndex{18}\)

Solve: \(16y^2=32y^3+2y\).

\(y=0,\space y=14\)

Solve Equations with Polynomial Functions

As our study of polynomial functions continues, it will often be important to know when the function will have a certain value or what points lie on the graph of the function. Our work with the Zero Product Property will be help us find these answers.

Example \(\PageIndex{19}\)

For the function \(f(x)=x^2+2x−2\),

ⓐ find \(x\) when \(f(x)=6\) ⓑ find two points that lie on the graph of the function.

ⓐ \(\begin{array} {ll} &f(x)=x^2+2x−2 \\ \text{Substitute }6\text{ for }f(x). &6=x^2+2x−2 \\ \text{Put the quadratic in standard form.} &x^2+2x−8=0 \\ \text{Factor the trinomial.} &(x+4)(x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &x−2=0 \\ x=−4 &\text{or} &x=2 \end{array} \\ \text{Check:} & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ \begin{array} {lll} \quad &\hspace{3mm} f(x)=x^2+2x−2 &f(x)=x^2+2x−2 \\ \quad &f(−4)=(−4)^2+2(−4)−2 &f(2)=2^2+2·2−2 \\ \quad &f(−4)=16−8−2 &f(2)=4+4−2 \\ \quad &f(−4)=6\checkmark &f(2)=6\checkmark \end{array} & \end{array} \) ⓑ Since \(f(−4)=6\) and \(f(2)=6\), the points \((−4,6)\) and \((2,6)\) lie on the graph of the function.

Example \(\PageIndex{20}\)

For the function \(f(x)=x^2−2x−8\),

ⓐ find \(x\) when \(f(x)=7\) ⓑ Find two points that lie on the graph of the function.

ⓐ \(x=−3\) or \(x=5\) ⓑ \((−3,7)\space (5,7)\)

Example \(\PageIndex{21}\)

For the function \(f(x)=x^2−8x+3\),

ⓐ find \(x\) when \(f(x)=−4\) ⓑ Find two points that lie on the graph of the function.

ⓐ \(x=1\) or \(x=7\) ⓑ \((1,−4)\space (7,−4)\)

The Zero Product Property also helps us determine where the function is zero. A value of \(x\) where the function is \(0\), is called a zero of the function .

ZERO OF A FUNCTION

For any function \(f\), if \(f(x)=0\), then \(x\) is a zero of the function .

When \(f(x)=0\), the point \((x,0)\) is a point on the graph. This point is an \(x\)- intercept of the graph. It is often important to know where the graph of a function crosses the axes. We will see some examples later.

Example \(\PageIndex{22}\)

For the function \(f(x)=3x^2+10x−8\), find

ⓐ the zeros of the function, ⓑ any \(x\)-intercepts of the graph of the function ⓒ any \(y\)-intercepts of the graph of the function

ⓐ To find the zeros of the function, we need to find when the function value is 0. \(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Substitute }0\text{ for}f(x). &0=3x^2+10x−8 \\ \text{Factor the trinomial.} &(x+4)(3x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &3x−2=0 \\ x=−4 &\text{or} &x=\frac{2}{3} \end{array} \end{array}\) ⓑ An \(x\)-intercept occurs when \(y=0\). Since \(f(−4)=0\) and \(f(\frac{2}{3})=0\), the points \((−4,0)\) and \((\frac{2}{3},0)\) lie on the graph. These points are \(x\)-intercepts of the function. ⓒ A \(y\)-intercept occurs when \(x=0\). To find the \(y\)-intercepts we need to find \(f(0)\). \(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Find }f(0)\text{ by substituting }0\text{ for }x. &f(0)=3·0^2+10·0−8 \\ \text{Simplify.} &f(0)=−8 \end{array} \) Since \(f(0)=−8\), the point \((0,−8)\) lies on the graph. This point is the \(y\)-intercept of the function.

Example \(\PageIndex{23}\)

For the function \(f(x)=2x^2−7x+5\), find

ⓐ the zeros of the function ⓑ any \(x\)-intercepts of the graph of the function ⓒ any \(y\)-intercepts of the graph of the function.

ⓐ \(x=1\) or \(x=\frac{5}{2}\) ⓑ \((1,0),\space (\frac{5}{2},0)\) ⓒ \((0,5)\)

Example \(\PageIndex{24}\)

For the function \(f(x)=6x^2+13x−15\), find

ⓐ \(x=−3\) or \(x=\frac{5}{6}\) ⓑ \((−3,0),\space (\frac{5}{6},0)\) ⓒ \((0,−15)\)

Solve Applications Modeled by Polynomial Equations

The problem-solving strategy we used earlier for applications that translate to linear equations will work just as well for applications that translate to polynomial equations. We will copy the problem-solving strategy here so we can use it for reference.

USE A PROBLEM SOLVING STRATEGY TO SOLVE WORD PROBLEMS.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using appropriate algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

We will start with a number problem to get practice translating words into a polynomial equation.

Example \(\PageIndex{25}\)

The product of two consecutive odd integers is 323. Find the integers.

\(\begin{array} {ll} \textbf{Step 1. Read }\text{the problem.} & \\ \textbf{Step 2. Identify }\text{what we are looking for.} &\text{We are looking for two consecutive integers.} \\ \textbf{Step 3. Name}\text{ what we are looking for.} &\text{Let } n=\text{ the first integer.} \\ &n+2= \text{ next consecutive odd integer} \\ \begin{array} {l} \textbf{Step 4. Translate }\text{into an equation. Restate the}\hspace{20mm} \\ \text{problem in a sentence.} \end{array} &\begin{array} {l} \text{The product of the two consecutive odd} \\ \text{integers is }323. \end{array} \\ &\quad n(n+2)=323 \\ \textbf{Step 5. Solve }\text{the equation.} n^2+2n=323 \\ \text{Bring all the terms to one side.} &n^2+2n−323=0 \\ \text{Factor the trinomial.} &(n−17)(n+19)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve the equations.} \end{array} &\begin{array} {ll} n−17=0 \hspace{10mm}&n+19=0 \\ n=17 &n=−19 \end{array} \end{array} \) There are two values for \(n\) that are solutions to this problem. So there are two sets of consecutive odd integers that will work.

\(\begin{array} {ll} \text{If the first integer is } n=17 \hspace{60mm} &\text{If the first integer is } n=-19 \\ \text{then the next odd integer is} &\text{then the next odd integer is} \\ \hspace{53mm} n+2 &\hspace{53mm} n+2 \\ \hspace{51mm} 17+2 &\hspace{51mm} -19+2 \\ \hspace{55mm} 19 &\hspace{55mm} -17 \\ \hspace{51mm} 17,19 &\hspace{51mm} -17,-19 \\ \textbf{Step 6. Check }\text{the answer.} & \\ \text{The results are consecutive odd integers} & \\ \begin{array} {ll} 17,\space 19\text{ and }−19,\space −17. & \\ 17·19=323\checkmark &−19(−17)=323\checkmark \end{array} & \\ \text{Both pairs of consecutive integers are solutions.} & \\ \textbf{Step 7. Answer }\text{the question} &\text{The consecutive integers are }17, 19\text{ and }−19,−17. \end{array} \)

Example \(\PageIndex{26}\)

The product of two consecutive odd integers is 255. Find the integers.

\(−15,−17\) and \(15, 17\)

Example \(\PageIndex{27}\)

The product of two consecutive odd integers is 483 Find the integers.

\(−23,−21\) and \(21, 23\)

Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give positive results.

In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.

Example \(\PageIndex{28}\)

A rectangular bedroom has an area 117 square feet. The length of the bedroom is four feet more than the width. Find the length and width of the bedroom.

Example \(\PageIndex{29}\)

A rectangular sign has area 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.

The width is 5 feet and length is 6 feet.

Example \(\PageIndex{30}\)

A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

The length of the patio is 12 feet and the width 15 feet.

In the next example, we will use the Pythagorean Theorem \((a^2+b^2=c^2)\). This formula gives the relation between the legs and the hypotenuse of a right triangle.

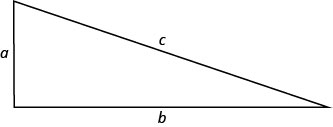
We will use this formula to in the next example.

Example \(\PageIndex{31}\)

A boat’s sail is in the shape of a right triangle as shown. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the sail.

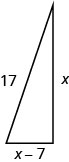
Example \(\PageIndex{32}\)

Justine wants to put a deck in the corner of her backyard in the shape of a right triangle. The length of one side of the deck is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the deck.

5 feet and 12 feet

Example \(\PageIndex{33}\)

A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of the other leg. Find the lengths of the hypotenuse and the other leg.

24 feet and 25 feet

The next example uses the function that gives the height of an object as a function of time when it is thrown from 80 feet above the ground.

Example \(\PageIndex{34}\)

Dennis is going to throw his rubber band ball upward from the top of a campus building. When he throws the rubber band ball from 80 feet above the ground, the function \(h(t)=−16t^2+64t+80\) models the height, \(h\), of the ball above the ground as a function of time, \(t\). Find:

ⓐ the zeros of this function which tell us when the ball hits the ground ⓑ when the ball will be 80 feet above the ground ⓒ the height of the ball at \(t=2\) seconds.

ⓐ The zeros of this function are found by solving \(h(t)=0\). This will tell us when the ball will hit the ground. \(\begin{array} {ll} &h(t)=0 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=0 \\ \text{Factor the GCF, }−16. &−16(t^2−4t−5)=0 \\ \text{Factor the trinomial.} &−16(t−5)(t+1)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.} \end{array} &\begin{array} {ll} t−5=0 &t+1=0 \\ t=5 &t=−1 \end{array} \end{array} \)

The result \(t=5\) tells us the ball will hit the ground 5 seconds after it is thrown. Since time cannot be negative, the result \(t=−1\) is discarded.

ⓑ The ball will be 80 feet above the ground when \(h(t)=80\). \(\begin{array} {ll} &h(t)=80 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=80 \\ \text{Subtract 80 from both sides.} &−16t^2+64t=0 \\ \text{Factor the GCF, }−16t. &−16t(t−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.}\end{array} &\begin{array} {ll} −16t=0 &t−4=0 \\ t=0 &t=4 \end{array} \\ &\text{The ball will be at 80 feet the moment Dennis} \\ &\text{tosses the ball and then 4 seconds later, when} \\ &\text{the ball is falling.} \end{array} \)

ⓒ To find the height ball at \(t=2\) seconds we find \(h(2)\). \(\begin{array} {ll} &h(t)=−16t^2+64t+80 \\ \text{To find }h(2)\text{ substitute }2\text{ for }t. &h(2)=−16(2)^2+64·2+80 \\ \text{Simplify.} &h(2)=144 \\ &\text{After 2 seconds, the ball will be at 144 feet.} \end{array}\)

Example \(\PageIndex{35}\)

Genevieve is going to throw a rock from the top a trail overlooking the ocean. When she throws the rock upward from 160 feet above the ocean, the function \(h(t)=−16t^2+48t+160\) models the height, \(h\), of the rock above the ocean as a function of time, \(t\). Find:

ⓐ the zeros of this function which tell us when the rock will hit the ocean ⓑ when the rock will be 160 feet above the ocean. ⓒ the height of the rock at \(t=1.5\) seconds.

ⓐ 5 ⓑ 0;3 ⓒ 196

Example \(\PageIndex{36}\)

Calib is going to throw his lucky penny from his balcony on a cruise ship. When he throws the penny upward from 128 feet above the ground, the function \(h(t)=−16t^2+32t+128\) models the height, \(h\), of the penny above the ocean as a function of time, \(t\). Find:

ⓐ the zeros of this function which is when the penny will hit the ocean ⓑ when the penny will be 128 feet above the ocean. ⓒ the height the penny will be at \(t=1\) seconds which is when the penny will be at its highest point.

ⓐ 4 ⓑ 0;2 ⓒ 144

Access this online resource for additional instruction and practice with quadratic equations.

• Beginning Algebra & Solving Quadratics with the Zero Property

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3
• How do you solve algebraic expressions?
• To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
• What are the basics of algebra?
• The basics of algebra are the commutative, associative, and distributive laws.
• What are the 3 rules of algebra?
• The basic rules of algebra are the commutative, associative, and distributive laws.
• What is the golden rule of algebra?
• The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
• What are the 5 basic laws of algebra?
• The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

algebra-calculator

• High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...

Please add a message.

Message received. Thanks for the feedback.