chi squared test of hypothesis

Hypothesis Testing - Chi Squared Test

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific tests considered here are called chi-square tests and are appropriate when the outcome is discrete (dichotomous, ordinal or categorical). For example, in some clinical trials the outcome is a classification such as hypertensive, pre-hypertensive or normotensive. We could use the same classification in an observational study such as the Framingham Heart Study to compare men and women in terms of their blood pressure status - again using the classification of hypertensive, pre-hypertensive or normotensive status.  

The technique to analyze a discrete outcome uses what is called a chi-square test. Specifically, the test statistic follows a chi-square probability distribution. We will consider chi-square tests here with one, two and more than two independent comparison groups.

Learning Objectives

After completing this module, the student will be able to:

• Perform chi-square tests by hand
• Appropriately interpret results of chi-square tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

Tests with One Sample, Discrete Outcome

Here we consider hypothesis testing with a discrete outcome variable in a single population. Discrete variables are variables that take on more than two distinct responses or categories and the responses can be ordered or unordered (i.e., the outcome can be ordinal or categorical). The procedure we describe here can be used for dichotomous (exactly 2 response options), ordinal or categorical discrete outcomes and the objective is to compare the distribution of responses, or the proportions of participants in each response category, to a known distribution. The known distribution is derived from another study or report and it is again important in setting up the hypotheses that the comparator distribution specified in the null hypothesis is a fair comparison. The comparator is sometimes called an external or a historical control.   

In one sample tests for a discrete outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the proportions of participants in each response

Test Statistic for Testing H 0 : p 1 = p 10 , p 2 = p 20 , ..., p k = p k0

We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1. In the test statistic, O = observed frequency and E=expected frequency in each of the response categories. The observed frequencies are those observed in the sample and the expected frequencies are computed as described below. χ 2 (chi-square) is another probability distribution and ranges from 0 to ∞. The test above statistic formula above is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories.  

When we conduct a χ 2 test, we compare the observed frequencies in each response category to the frequencies we would expect if the null hypothesis were true. These expected frequencies are determined by allocating the sample to the response categories according to the distribution specified in H 0 . This is done by multiplying the observed sample size (n) by the proportions specified in the null hypothesis (p 10 , p 20 , ..., p k0 ). To ensure that the sample size is appropriate for the use of the test statistic above, we need to ensure that the following: min(np 10 , n p 20 , ..., n p k0 ) > 5.  

The test of hypothesis with a discrete outcome measured in a single sample, where the goal is to assess whether the distribution of responses follows a known distribution, is called the χ 2 goodness-of-fit test. As the name indicates, the idea is to assess whether the pattern or distribution of responses in the sample "fits" a specified population (external or historical) distribution. In the next example we illustrate the test. As we work through the example, we provide additional details related to the use of this new test statistic.  

A University conducted a survey of its recent graduates to collect demographic and health information for future planning purposes as well as to assess students' satisfaction with their undergraduate experiences. The survey revealed that a substantial proportion of students were not engaging in regular exercise, many felt their nutrition was poor and a substantial number were smoking. In response to a question on regular exercise, 60% of all graduates reported getting no regular exercise, 25% reported exercising sporadically and 15% reported exercising regularly as undergraduates. The next year the University launched a health promotion campaign on campus in an attempt to increase health behaviors among undergraduates. The program included modules on exercise, nutrition and smoking cessation. To evaluate the impact of the program, the University again surveyed graduates and asked the same questions. The survey was completed by 470 graduates and the following data were collected on the exercise question:

Based on the data, is there evidence of a shift in the distribution of responses to the exercise question following the implementation of the health promotion campaign on campus? Run the test at a 5% level of significance.

In this example, we have one sample and a discrete (ordinal) outcome variable (with three response options). We specifically want to compare the distribution of responses in the sample to the distribution reported the previous year (i.e., 60%, 25%, 15% reporting no, sporadic and regular exercise, respectively). We now run the test using the five-step approach.  

• Step 1. Set up hypotheses and determine level of significance.

The null hypothesis again represents the "no change" or "no difference" situation. If the health promotion campaign has no impact then we expect the distribution of responses to the exercise question to be the same as that measured prior to the implementation of the program.

H 0 : p 1 =0.60, p 2 =0.25, p 3 =0.15,  or equivalently H 0 : Distribution of responses is 0.60, 0.25, 0.15  

H 1 :   H 0 is false.          α =0.05

Notice that the research hypothesis is written in words rather than in symbols. The research hypothesis as stated captures any difference in the distribution of responses from that specified in the null hypothesis. We do not specify a specific alternative distribution, instead we are testing whether the sample data "fit" the distribution in H 0 or not. With the χ 2 goodness-of-fit test there is no upper or lower tailed version of the test.

• Step 2. Select the appropriate test statistic.  

The test statistic is:

We must first assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=470 and the proportions specified in the null hypothesis are 0.60, 0.25 and 0.15. Thus, min( 470(0.65), 470(0.25), 470(0.15))=min(282, 117.5, 70.5)=70.5. The sample size is more than adequate so the formula can be used.

• Step 3. Set up decision rule.  

The decision rule for the χ 2 test depends on the level of significance and the degrees of freedom, defined as degrees of freedom (df) = k-1 (where k is the number of response categories). If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. Critical values can be found in a table of probabilities for the χ 2 distribution. Here we have df=k-1=3-1=2 and a 5% level of significance. The appropriate critical value is 5.99, and the decision rule is as follows: Reject H 0 if χ 2 > 5.99.

• Step 4. Compute the test statistic.  

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) and the expected frequencies into the formula for the test statistic identified in Step 2. The computations can be organized as follows.

Notice that the expected frequencies are taken to one decimal place and that the sum of the observed frequencies is equal to the sum of the expected frequencies. The test statistic is computed as follows:

• Step 5. Conclusion.  

We reject H 0 because 8.46 > 5.99. We have statistically significant evidence at α=0.05 to show that H 0 is false, or that the distribution of responses is not 0.60, 0.25, 0.15.  The p-value is p < 0.005.  

In the χ 2 goodness-of-fit test, we conclude that either the distribution specified in H 0 is false (when we reject H 0 ) or that we do not have sufficient evidence to show that the distribution specified in H 0 is false (when we fail to reject H 0 ). Here, we reject H 0 and concluded that the distribution of responses to the exercise question following the implementation of the health promotion campaign was not the same as the distribution prior. The test itself does not provide details of how the distribution has shifted. A comparison of the observed and expected frequencies will provide some insight into the shift (when the null hypothesis is rejected). Does it appear that the health promotion campaign was effective?  

Consider the following: 

If the null hypothesis were true (i.e., no change from the prior year) we would have expected more students to fall in the "No Regular Exercise" category and fewer in the "Regular Exercise" categories. In the sample, 255/470 = 54% reported no regular exercise and 90/470=19% reported regular exercise. Thus, there is a shift toward more regular exercise following the implementation of the health promotion campaign. There is evidence of a statistical difference, is this a meaningful difference? Is there room for improvement?

The National Center for Health Statistics (NCHS) provided data on the distribution of weight (in categories) among Americans in 2002. The distribution was based on specific values of body mass index (BMI) computed as weight in kilograms over height in meters squared. Underweight was defined as BMI< 18.5, Normal weight as BMI between 18.5 and 24.9, overweight as BMI between 25 and 29.9 and obese as BMI of 30 or greater. Americans in 2002 were distributed as follows: 2% Underweight, 39% Normal Weight, 36% Overweight, and 23% Obese. Suppose we want to assess whether the distribution of BMI is different in the Framingham Offspring sample. Using data from the n=3,326 participants who attended the seventh examination of the Offspring in the Framingham Heart Study we created the BMI categories as defined and observed the following:

• Step 1.  Set up hypotheses and determine level of significance.

H 0 : p 1 =0.02, p 2 =0.39, p 3 =0.36, p 4 =0.23     or equivalently

H 0 : Distribution of responses is 0.02, 0.39, 0.36, 0.23

H 1 :   H 0 is false.        α=0.05

The formula for the test statistic is:

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=3,326 and the proportions specified in the null hypothesis are 0.02, 0.39, 0.36 and 0.23. Thus, min( 3326(0.02), 3326(0.39), 3326(0.36), 3326(0.23))=min(66.5, 1297.1, 1197.4, 765.0)=66.5. The sample size is more than adequate, so the formula can be used.

Here we have df=k-1=4-1=3 and a 5% level of significance. The appropriate critical value is 7.81 and the decision rule is as follows: Reject H 0 if χ 2 > 7.81.

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) into the formula for the test statistic identified in Step 2. We organize the computations in the following table.

The test statistic is computed as follows:

We reject H 0 because 233.53 > 7.81. We have statistically significant evidence at α=0.05 to show that H 0 is false or that the distribution of BMI in Framingham is different from the national data reported in 2002, p < 0.005.  

Again, the χ 2   goodness-of-fit test allows us to assess whether the distribution of responses "fits" a specified distribution. Here we show that the distribution of BMI in the Framingham Offspring Study is different from the national distribution. To understand the nature of the difference we can compare observed and expected frequencies or observed and expected proportions (or percentages). The frequencies are large because of the large sample size, the observed percentages of patients in the Framingham sample are as follows: 0.6% underweight, 28% normal weight, 41% overweight and 30% obese. In the Framingham Offspring sample there are higher percentages of overweight and obese persons (41% and 30% in Framingham as compared to 36% and 23% in the national data), and lower proportions of underweight and normal weight persons (0.6% and 28% in Framingham as compared to 2% and 39% in the national data). Are these meaningful differences?

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable in a single population. We presented a test using a test statistic Z to test whether an observed (sample) proportion differed significantly from a historical or external comparator. The chi-square goodness-of-fit test can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square goodness-of-fit test.

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

We presented the following approach to the test using a Z statistic. 

• Step 1. Set up hypotheses and determine level of significance

H 0 : p = 0.75

H 1 : p ≠ 0.75                               α=0.05

We must first check that the sample size is adequate. Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 125(0.75), 125(1-0.75))=min(94, 31)=31. The sample size is more than adequate so the following formula can be used

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. The sample proportion is:

We reject H 0 because -6.15 < -1.960. We have statistically significant evidence at a =0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001).  

We now conduct the same test using the chi-square goodness-of-fit test. First, we summarize our sample data as follows:

H 0 : p 1 =0.75, p 2 =0.25     or equivalently H 0 : Distribution of responses is 0.75, 0.25 

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ...,np k >) > 5. The sample size here is n=125 and the proportions specified in the null hypothesis are 0.75, 0.25. Thus, min( 125(0.75), 125(0.25))=min(93.75, 31.25)=31.25. The sample size is more than adequate so the formula can be used.

Here we have df=k-1=2-1=1 and a 5% level of significance. The appropriate critical value is 3.84, and the decision rule is as follows: Reject H 0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

(Note that (-6.15) 2 = 37.8, where -6.15 was the value of the Z statistic in the test for proportions shown above.)

We reject H 0 because 37.8 > 3.84. We have statistically significant evidence at α=0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data.  (p < 0.0001). This is the same conclusion we reached when we conducted the test using the Z test above. With a dichotomous outcome, Z 2 = χ 2 !   In statistics, there are often several approaches that can be used to test hypotheses. 

Tests for Two or More Independent Samples, Discrete Outcome

Here we extend that application of the chi-square test to the case with two or more independent comparison groups. Specifically, the outcome of interest is discrete with two or more responses and the responses can be ordered or unordered (i.e., the outcome can be dichotomous, ordinal or categorical). We now consider the situation where there are two or more independent comparison groups and the goal of the analysis is to compare the distribution of responses to the discrete outcome variable among several independent comparison groups.  

The test is called the χ 2 test of independence and the null hypothesis is that there is no difference in the distribution of responses to the outcome across comparison groups. This is often stated as follows: The outcome variable and the grouping variable (e.g., the comparison treatments or comparison groups) are independent (hence the name of the test). Independence here implies homogeneity in the distribution of the outcome among comparison groups.    

The null hypothesis in the χ 2 test of independence is often stated in words as: H 0 : The distribution of the outcome is independent of the groups. The alternative or research hypothesis is that there is a difference in the distribution of responses to the outcome variable among the comparison groups (i.e., that the distribution of responses "depends" on the group). In order to test the hypothesis, we measure the discrete outcome variable in each participant in each comparison group. The data of interest are the observed frequencies (or number of participants in each response category in each group). The formula for the test statistic for the χ 2 test of independence is given below.

Test Statistic for Testing H 0 : Distribution of outcome is independent of groups

and we find the critical value in a table of probabilities for the chi-square distribution with df=(r-1)*(c-1).

Here O = observed frequency, E=expected frequency in each of the response categories in each group, r = the number of rows in the two-way table and c = the number of columns in the two-way table.   r and c correspond to the number of comparison groups and the number of response options in the outcome (see below for more details). The observed frequencies are the sample data and the expected frequencies are computed as described below. The test statistic is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories in each group.  

The data for the χ 2 test of independence are organized in a two-way table. The outcome and grouping variable are shown in the rows and columns of the table. The sample table below illustrates the data layout. The table entries (blank below) are the numbers of participants in each group responding to each response category of the outcome variable.

Table - Possible outcomes are are listed in the columns; The groups being compared are listed in rows.

In the table above, the grouping variable is shown in the rows of the table; r denotes the number of independent groups. The outcome variable is shown in the columns of the table; c denotes the number of response options in the outcome variable. Each combination of a row (group) and column (response) is called a cell of the table. The table has r*c cells and is sometimes called an r x c ("r by c") table. For example, if there are 4 groups and 5 categories in the outcome variable, the data are organized in a 4 X 5 table. The row and column totals are shown along the right-hand margin and the bottom of the table, respectively. The total sample size, N, can be computed by summing the row totals or the column totals. Similar to ANOVA, N does not refer to a population size here but rather to the total sample size in the analysis. The sample data can be organized into a table like the above. The numbers of participants within each group who select each response option are shown in the cells of the table and these are the observed frequencies used in the test statistic.

The test statistic for the χ 2 test of independence involves comparing observed (sample data) and expected frequencies in each cell of the table. The expected frequencies are computed assuming that the null hypothesis is true. The null hypothesis states that the two variables (the grouping variable and the outcome) are independent. The definition of independence is as follows:

 Two events, A and B, are independent if P(A|B) = P(A), or equivalently, if P(A and B) = P(A) P(B).

The second statement indicates that if two events, A and B, are independent then the probability of their intersection can be computed by multiplying the probability of each individual event. To conduct the χ 2 test of independence, we need to compute expected frequencies in each cell of the table. Expected frequencies are computed by assuming that the grouping variable and outcome are independent (i.e., under the null hypothesis). Thus, if the null hypothesis is true, using the definition of independence:

P(Group 1 and Response Option 1) = P(Group 1) P(Response Option 1).

 The above states that the probability that an individual is in Group 1 and their outcome is Response Option 1 is computed by multiplying the probability that person is in Group 1 by the probability that a person is in Response Option 1. To conduct the χ 2 test of independence, we need expected frequencies and not expected probabilities . To convert the above probability to a frequency, we multiply by N. Consider the following small example.

The data shown above are measured in a sample of size N=150. The frequencies in the cells of the table are the observed frequencies. If Group and Response are independent, then we can compute the probability that a person in the sample is in Group 1 and Response category 1 using:

P(Group 1 and Response 1) = P(Group 1) P(Response 1),

P(Group 1 and Response 1) = (25/150) (62/150) = 0.069.

Thus if Group and Response are independent we would expect 6.9% of the sample to be in the top left cell of the table (Group 1 and Response 1). The expected frequency is 150(0.069) = 10.4.   We could do the same for Group 2 and Response 1:

P(Group 2 and Response 1) = P(Group 2) P(Response 1),

P(Group 2 and Response 1) = (50/150) (62/150) = 0.138.

The expected frequency in Group 2 and Response 1 is 150(0.138) = 20.7.

Thus, the formula for determining the expected cell frequencies in the χ 2 test of independence is as follows:

Expected Cell Frequency = (Row Total * Column Total)/N.

The above computes the expected frequency in one step rather than computing the expected probability first and then converting to a frequency.  

In a prior example we evaluated data from a survey of university graduates which assessed, among other things, how frequently they exercised. The survey was completed by 470 graduates. In the prior example we used the χ 2 goodness-of-fit test to assess whether there was a shift in the distribution of responses to the exercise question following the implementation of a health promotion campaign on campus. We specifically considered one sample (all students) and compared the observed distribution to the distribution of responses the prior year (a historical control). Suppose we now wish to assess whether there is a relationship between exercise on campus and students' living arrangements. As part of the same survey, graduates were asked where they lived their senior year. The response options were dormitory, on-campus apartment, off-campus apartment, and at home (i.e., commuted to and from the university). The data are shown below.

Based on the data, is there a relationship between exercise and student's living arrangement? Do you think where a person lives affect their exercise status? Here we have four independent comparison groups (living arrangement) and a discrete (ordinal) outcome variable with three response options. We specifically want to test whether living arrangement and exercise are independent. We will run the test using the five-step approach.  

H 0 : Living arrangement and exercise are independent

H 1 : H 0 is false.                α=0.05

The null and research hypotheses are written in words rather than in symbols. The research hypothesis is that the grouping variable (living arrangement) and the outcome variable (exercise) are dependent or related.   

• Step 2.  Select the appropriate test statistic.  

The condition for appropriate use of the above test statistic is that each expected frequency is at least 5. In Step 4 we will compute the expected frequencies and we will ensure that the condition is met.

The decision rule depends on the level of significance and the degrees of freedom, defined as df = (r-1)(c-1), where r and c are the numbers of rows and columns in the two-way data table.   The row variable is the living arrangement and there are 4 arrangements considered, thus r=4. The column variable is exercise and 3 responses are considered, thus c=3. For this test, df=(4-1)(3-1)=3(2)=6. Again, with χ 2 tests there are no upper, lower or two-tailed tests. If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. The rejection region for the χ 2 test of independence is always in the upper (right-hand) tail of the distribution. For df=6 and a 5% level of significance, the appropriate critical value is 12.59 and the decision rule is as follows: Reject H 0 if c 2 > 12.59.

We now compute the expected frequencies using the formula,

Expected Frequency = (Row Total * Column Total)/N.

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency.   The expected frequencies are shown in parentheses.

Notice that the expected frequencies are taken to one decimal place and that the sums of the observed frequencies are equal to the sums of the expected frequencies in each row and column of the table.  

Recall in Step 2 a condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 9.6) and therefore it is appropriate to use the test statistic.

We reject H 0 because 60.5 > 12.59. We have statistically significant evidence at a =0.05 to show that H 0 is false or that living arrangement and exercise are not independent (i.e., they are dependent or related), p < 0.005.  

Again, the χ 2 test of independence is used to test whether the distribution of the outcome variable is similar across the comparison groups. Here we rejected H 0 and concluded that the distribution of exercise is not independent of living arrangement, or that there is a relationship between living arrangement and exercise. The test provides an overall assessment of statistical significance. When the null hypothesis is rejected, it is important to review the sample data to understand the nature of the relationship. Consider again the sample data. 

Because there are different numbers of students in each living situation, it makes the comparisons of exercise patterns difficult on the basis of the frequencies alone. The following table displays the percentages of students in each exercise category by living arrangement. The percentages sum to 100% in each row of the table. For comparison purposes, percentages are also shown for the total sample along the bottom row of the table.

From the above, it is clear that higher percentages of students living in dormitories and in on-campus apartments reported regular exercise (31% and 23%) as compared to students living in off-campus apartments and at home (10% each).  

Test Yourself

 Pancreaticoduodenectomy (PD) is a procedure that is associated with considerable morbidity. A study was recently conducted on 553 patients who had a successful PD between January 2000 and December 2010 to determine whether their Surgical Apgar Score (SAS) is related to 30-day perioperative morbidity and mortality. The table below gives the number of patients experiencing no, minor, or major morbidity by SAS category.  

Question: What would be an appropriate statistical test to examine whether there is an association between Surgical Apgar Score and patient outcome? Using 14.13 as the value of the test statistic for these data, carry out the appropriate test at a 5% level of significance. Show all parts of your test.

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable and two independent comparison groups. We presented a test using a test statistic Z to test for equality of independent proportions. The chi-square test of independence can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square test of independence.

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We tested whether there was a significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using a Z statistic, as follows. 

H 0 : p 1 = p 2    

H 1 : p 1 ≠ p 2                             α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group or that:

In this example, we have

Therefore, the sample size is adequate, so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5.  Conclusion.  

We now conduct the same test using the chi-square test of independence.  

H 0 : Treatment and outcome (meaningful reduction in pain) are independent

H 1 :   H 0 is false.         α=0.05

The formula for the test statistic is:  

For this test, df=(2-1)(2-1)=1. At a 5% level of significance, the appropriate critical value is 3.84 and the decision rule is as follows: Reject H0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

We now compute the expected frequencies using:

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.

A condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 22.0) and therefore it is appropriate to use the test statistic.

(Note that (2.53) 2 = 6.4, where 2.53 was the value of the Z statistic in the test for proportions shown above.)

Chi-Squared Tests in R

The video below by Mike Marin demonstrates how to perform chi-squared tests in the R programming language.

Answer to Problem on Pancreaticoduodenectomy and Surgical Apgar Scores

We have 3 independent comparison groups (Surgical Apgar Score) and a categorical outcome variable (morbidity/mortality). We can run a Chi-Squared test of independence.

H 0 : Apgar scores and patient outcome are independent of one another.

H A : Apgar scores and patient outcome are not independent.

Chi-squared = 14.3

Since 14.3 is greater than 9.49, we reject H 0.

There is an association between Apgar scores and patient outcome. The lowest Apgar score group (0 to 4) experienced the highest percentage of major morbidity or mortality (16 out of 57=28%) compared to the other Apgar score groups.

Chi-Square (Χ²) Test & How To Calculate Formula Equation

Benjamin Frimodig

Science Expert

B.A., History and Science, Harvard University

Ben Frimodig is a 2021 graduate of Harvard College, where he studied the History of Science.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

On This Page:

Chi-square (χ2) is used to test hypotheses about the distribution of observations into categories with no inherent ranking.

What Is a Chi-Square Statistic?

The Chi-square test (pronounced Kai) looks at the pattern of observations and will tell us if certain combinations of the categories occur more frequently than we would expect by chance, given the total number of times each category occurred.

It looks for an association between the variables. We cannot use a correlation coefficient to look for the patterns in this data because the categories often do not form a continuum.

There are three main types of Chi-square tests, tests of goodness of fit, the test of independence, and the test for homogeneity. All three tests rely on the same formula to compute a test statistic.

These tests function by deciphering relationships between observed sets of data and theoretical or “expected” sets of data that align with the null hypothesis.

What is a Contingency Table?

Contingency tables (also known as two-way tables) are grids in which Chi-square data is organized and displayed. They provide a basic picture of the interrelation between two variables and can help find interactions between them.

In contingency tables, one variable and each of its categories are listed vertically, and the other variable and each of its categories are listed horizontally.

Additionally, including column and row totals, also known as “marginal frequencies,” will help facilitate the Chi-square testing process.

In order for the Chi-square test to be considered trustworthy, each cell of your expected contingency table must have a value of at least five.

Each Chi-square test will have one contingency table representing observed counts (see Fig. 1) and one contingency table representing expected counts (see Fig. 2).

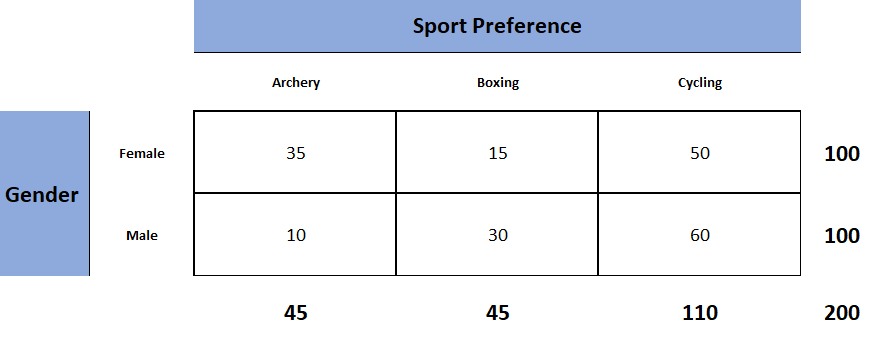
Figure 1. Observed table (which contains the observed counts).

To obtain the expected frequencies for any cell in any cross-tabulation in which the two variables are assumed independent, multiply the row and column totals for that cell and divide the product by the total number of cases in the table.

Figure 2. Expected table (what we expect the two-way table to look like if the two categorical variables are independent).

To decide if our calculated value for χ2 is significant, we also need to work out the degrees of freedom for our contingency table using the following formula: df= (rows – 1) x (columns – 1).

Formula Calculation

Calculate the chi-square statistic (χ2) by completing the following steps:

• Calculate the expected frequencies and the observed frequencies.
• For each observed number in the table, subtract the corresponding expected number (O — E).
• Square the difference (O —E)².
• Divide the squares obtained for each cell in the table by the expected number for that cell (O – E)² / E.
• Sum all the values for (O – E)² / E. This is the chi-square statistic.
• Calculate the degrees of freedom for the contingency table using the following formula; df= (rows – 1) x (columns – 1).

Once we have calculated the degrees of freedom (df) and the chi-squared value (χ2), we can use the χ2 table (often at the back of a statistics book) to check if our value for χ2 is higher than the critical value given in the table. If it is, then our result is significant at the level given.

Interpretation

The chi-square statistic tells you how much difference exists between the observed count in each table cell to the counts you would expect if there were no relationship at all in the population.

Small Chi-Square Statistic: If the chi-square statistic is small and the p-value is large (usually greater than 0.05), this often indicates that the observed frequencies in the sample are close to what would be expected under the null hypothesis.

The null hypothesis usually states no association between the variables being studied or that the observed distribution fits the expected distribution.

In theory, if the observed and expected values were equal (no difference), then the chi-square statistic would be zero — but this is unlikely to happen in real life.

Large Chi-Square Statistic : If the chi-square statistic is large and the p-value is small (usually less than 0.05), then the conclusion is often that the data does not fit the model well, i.e., the observed and expected values are significantly different. This often leads to the rejection of the null hypothesis.

How to Report

To report a chi-square output in an APA-style results section, always rely on the following template:

χ2 ( degrees of freedom , N = sample size ) = chi-square statistic value , p = p value .

In the case of the above example, the results would be written as follows:

A chi-square test of independence showed that there was a significant association between gender and post-graduation education plans, χ2 (4, N = 101) = 54.50, p < .001.

APA Style Rules

• Do not use a zero before a decimal when the statistic cannot be greater than 1 (proportion, correlation, level of statistical significance).
• Report exact p values to two or three decimals (e.g., p = .006, p = .03).
• However, report p values less than .001 as “ p < .001.”
• Put a space before and after a mathematical operator (e.g., minus, plus, greater than, less than, equals sign).
• Do not repeat statistics in both the text and a table or figure.

p -value Interpretation

You test whether a given χ2 is statistically significant by testing it against a table of chi-square distributions , according to the number of degrees of freedom for your sample, which is the number of categories minus 1. The chi-square assumes that you have at least 5 observations per category.

If you are using SPSS then you will have an expected p -value.

For a chi-square test, a p-value that is less than or equal to the .05 significance level indicates that the observed values are different to the expected values.

Thus, low p-values (p< .05) indicate a likely difference between the theoretical population and the collected sample. You can conclude that a relationship exists between the categorical variables.

Remember that p -values do not indicate the odds that the null hypothesis is true but rather provide the probability that one would obtain the sample distribution observed (or a more extreme distribution) if the null hypothesis was true.

A level of confidence necessary to accept the null hypothesis can never be reached. Therefore, conclusions must choose to either fail to reject the null or accept the alternative hypothesis, depending on the calculated p-value.

The four steps below show you how to analyze your data using a chi-square goodness-of-fit test in SPSS (when you have hypothesized that you have equal expected proportions).

Step 1 : Analyze > Nonparametric Tests > Legacy Dialogs > Chi-square… on the top menu as shown below:

Step 2 : Move the variable indicating categories into the “Test Variable List:” box.

Step 3 : If you want to test the hypothesis that all categories are equally likely, click “OK.”

Step 4 : Specify the expected count for each category by first clicking the “Values” button under “Expected Values.”

Step 5 : Then, in the box to the right of “Values,” enter the expected count for category one and click the “Add” button. Now enter the expected count for category two and click “Add.” Continue in this way until all expected counts have been entered.

Step 6 : Then click “OK.”

The four steps below show you how to analyze your data using a chi-square test of independence in SPSS Statistics.

Step 1 : Open the Crosstabs dialog (Analyze > Descriptive Statistics > Crosstabs).

Step 2 : Select the variables you want to compare using the chi-square test. Click one variable in the left window and then click the arrow at the top to move the variable. Select the row variable and the column variable.

Step 3 : Click Statistics (a new pop-up window will appear). Check Chi-square, then click Continue.

Step 4 : (Optional) Check the box for Display clustered bar charts.

Step 5 : Click OK.

Goodness-of-Fit Test

The Chi-square goodness of fit test is used to compare a randomly collected sample containing a single, categorical variable to a larger population.

This test is most commonly used to compare a random sample to the population from which it was potentially collected.

The test begins with the creation of a null and alternative hypothesis. In this case, the hypotheses are as follows:

Null Hypothesis (Ho) : The null hypothesis (Ho) is that the observed frequencies are the same (except for chance variation) as the expected frequencies. The collected data is consistent with the population distribution.

Alternative Hypothesis (Ha) : The collected data is not consistent with the population distribution.

The next step is to create a contingency table that represents how the data would be distributed if the null hypothesis were exactly correct.

The sample’s overall deviation from this theoretical/expected data will allow us to draw a conclusion, with a more severe deviation resulting in smaller p-values.

Test for Independence

The Chi-square test for independence looks for an association between two categorical variables within the same population.

Unlike the goodness of fit test, the test for independence does not compare a single observed variable to a theoretical population but rather two variables within a sample set to one another.

The hypotheses for a Chi-square test of independence are as follows:

Null Hypothesis (Ho) : There is no association between the two categorical variables in the population of interest.

Alternative Hypothesis (Ha) : There is no association between the two categorical variables in the population of interest.

The next step is to create a contingency table of expected values that reflects how a data set that perfectly aligns the null hypothesis would appear.

The simplest way to do this is to calculate the marginal frequencies of each row and column; the expected frequency of each cell is equal to the marginal frequency of the row and column that corresponds to a given cell in the observed contingency table divided by the total sample size.

Test for Homogeneity

The Chi-square test for homogeneity is organized and executed exactly the same as the test for independence.

The main difference to remember between the two is that the test for independence looks for an association between two categorical variables within the same population, while the test for homogeneity determines if the distribution of a variable is the same in each of several populations (thus allocating population itself as the second categorical variable).

Null Hypothesis (Ho) : There is no difference in the distribution of a categorical variable for several populations or treatments.

Alternative Hypothesis (Ha) : There is a difference in the distribution of a categorical variable for several populations or treatments.

The difference between these two tests can be a bit tricky to determine, especially in the practical applications of a Chi-square test. A reliable rule of thumb is to determine how the data was collected.

If the data consists of only one random sample with the observations classified according to two categorical variables, it is a test for independence. If the data consists of more than one independent random sample, it is a test for homogeneity.

What is the chi-square test?

The Chi-square test is a non-parametric statistical test used to determine if there’s a significant association between two or more categorical variables in a sample.

It works by comparing the observed frequencies in each category of a cross-tabulation with the frequencies expected under the null hypothesis, which assumes there is no relationship between the variables.

This test is often used in fields like biology, marketing, sociology, and psychology for hypothesis testing.

What does chi-square tell you?

The Chi-square test informs whether there is a significant association between two categorical variables. Suppose the calculated Chi-square value is above the critical value from the Chi-square distribution.

In that case, it suggests a significant relationship between the variables, rejecting the null hypothesis of no association.

How to calculate chi-square?

To calculate the Chi-square statistic, follow these steps:

1. Create a contingency table of observed frequencies for each category.

2. Calculate expected frequencies for each category under the null hypothesis.

3. Compute the Chi-square statistic using the formula: Χ² = Σ [ (O_i – E_i)² / E_i ], where O_i is the observed frequency and E_i is the expected frequency.

4. Compare the calculated statistic with the critical value from the Chi-square distribution to draw a conclusion.

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

The Chi-Square Test

What is a chi-square test.

A Chi-square test is a hypothesis testing method. Two common Chi-square tests involve checking if observed frequencies in one or more categories match expected frequencies.

Is a Chi-square test the same as a χ² test?

Yes, χ is the Greek symbol Chi.

What are my choices?

If you have a single measurement variable, you use a Chi-square goodness of fit test . If you have two measurement variables, you use a Chi-square test of independence . There are other Chi-square tests, but these two are the most common.

Types of Chi-square tests

You use a Chi-square test for hypothesis tests about whether your data is as expected. The basic idea behind the test is to compare the observed values in your data to the expected values that you would see if the null hypothesis is true.

There are two commonly used Chi-square tests: the Chi-square goodness of fit test and the Chi-square test of independence . Both tests involve variables that divide your data into categories. As a result, people can be confused about which test to use. The table below compares the two tests.

Visit the individual pages for each type of Chi-square test to see examples along with details on assumptions and calculations.

Table 1: Choosing a Chi-square test

How to perform a chi-square test.

For both the Chi-square goodness of fit test and the Chi-square test of independence , you perform the same analysis steps, listed below. Visit the pages for each type of test to see these steps in action.

• Define your null and alternative hypotheses before collecting your data.
• Decide on the alpha value. This involves deciding the risk you are willing to take of drawing the wrong conclusion. For example, suppose you set α=0.05 when testing for independence. Here, you have decided on a 5% risk of concluding the two variables are independent when in reality they are not.
• Check the data for errors.
• Check the assumptions for the test. (Visit the pages for each test type for more detail on assumptions.)
• Perform the test and draw your conclusion.

Both Chi-square tests in the table above involve calculating a test statistic. The basic idea behind the tests is that you compare the actual data values with what would be expected if the null hypothesis is true. The test statistic involves finding the squared difference between actual and expected data values, and dividing that difference by the expected data values. You do this for each data point and add up the values.

Then, you compare the test statistic to a theoretical value from the Chi-square distribution . The theoretical value depends on both the alpha value and the degrees of freedom for your data. Visit the pages for each test type for detailed examples.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.1: Chi-Square Tests for Independence

• Last updated
• Save as PDF
• Page ID 513

Learning Objectives

• To understand what chi-square distributions are.
• To understand how to use a chi-square test to judge whether two factors are independent.

Chi-Square Distributions

As you know, there is a whole family of \(t\)-distributions, each one specified by a parameter called the degrees of freedom, denoted \(df\). Similarly, all the chi-square distributions form a family, and each of its members is also specified by a parameter \(df\), the number of degrees of freedom. Chi is a Greek letter denoted by the symbol \(\chi\) and chi-square is often denoted by \(\chi^2\).

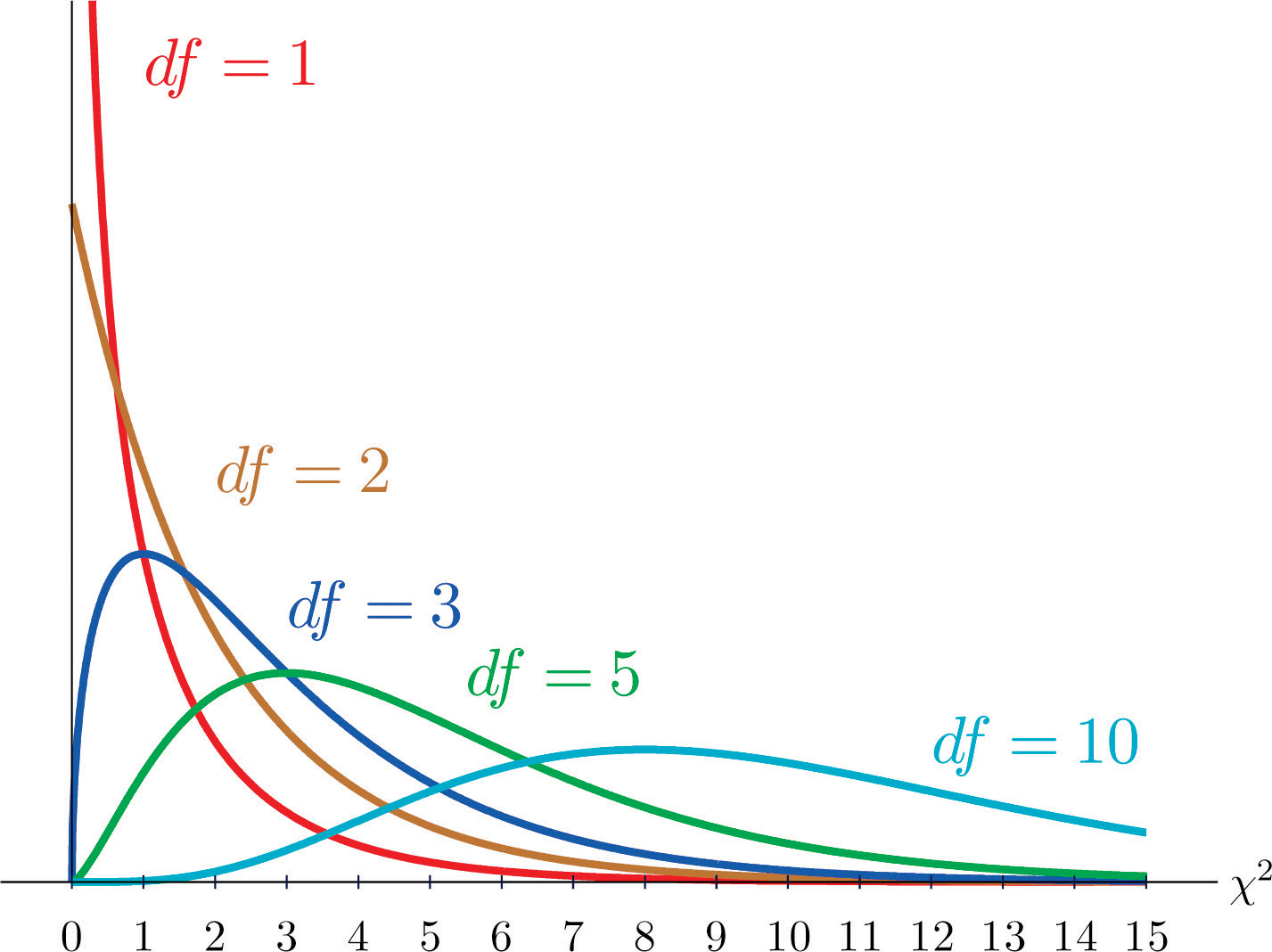
Figure \(\PageIndex{1}\) shows several \(\chi\)-square distributions for different degrees of freedom. A chi-square random variable is a random variable that assumes only positive values and follows a \(\chi\)-square distribution.

Definition: critical value

The value of the chi-square random variable \(\chi^2\) with \(df=k\) that cuts off a right tail of area \(c\) is denoted \(\chi_c^2\) and is called a critical value (Figure \(\PageIndex{2}\)).

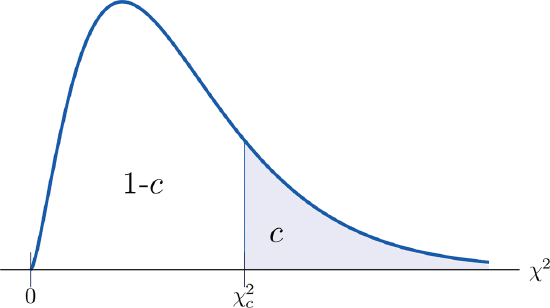
Figure \(\PageIndex{3}\) below gives values of \(\chi_c^2\) for various values of \(c\) and under several chi-square distributions with various degrees of freedom.

Tests for Independence

Hypotheses tests encountered earlier in the book had to do with how the numerical values of two population parameters compared. In this subsection we will investigate hypotheses that have to do with whether or not two random variables take their values independently, or whether the value of one has a relation to the value of the other. Thus the hypotheses will be expressed in words, not mathematical symbols. We build the discussion around the following example.

There is a theory that the gender of a baby in the womb is related to the baby’s heart rate: baby girls tend to have higher heart rates. Suppose we wish to test this theory. We examine the heart rate records of \(40\) babies taken during their mothers’ last prenatal checkups before delivery, and to each of these \(40\) randomly selected records we compute the values of two random measures: 1) gender and 2) heart rate. In this context these two random measures are often called factors. Since the burden of proof is that heart rate and gender are related, not that they are unrelated, the problem of testing the theory on baby gender and heart rate can be formulated as a test of the following hypotheses:

\[H_0: \text{Baby gender and baby heart rate are independent}\\ vs. \\ H_a: \text{Baby gender and baby heart rate are not independent} \nonumber \]

The factor gender has two natural categories or levels: boy and girl. We divide the second factor, heart rate, into two levels, low and high, by choosing some heart rate, say \(145\) beats per minute, as the cutoff between them. A heart rate below \(145\) beats per minute will be considered low and \(145\) and above considered high. The \(40\) records give rise to a \(2\times 2\) contingency table . By adjoining row totals, column totals, and a grand total we obtain the table shown as Table \(\PageIndex{1}\). The four entries in boldface type are counts of observations from the sample of \(n = 40\). There were \(11\) girls with low heart rate, \(17\) boys with low heart rate, and so on. They form the core of the expanded table.

In analogy with the fact that the probability of independent events is the product of the probabilities of each event, if heart rate and gender were independent then we would expect the number in each core cell to be close to the product of the row total \(R\) and column total \(C\) of the row and column containing it, divided by the sample size \(n\). Denoting such an expected number of observations \(E\), these four expected values are:

• 1 st row and 1 st column: \(E=(R\times C)/n = 18\times 28 /40 = 12.6\)
• 1 st row and 2 nd column: \(E=(R\times C)/n = 18\times 12 /40 = 5.4\)
• 2 nd row and 1 st column: \(E=(R\times C)/n = 22\times 28 /40 = 15.4\)
• 2 nd row and 2 nd column: \(E=(R\times C)/n = 22\times 12 /40 = 6.6\)

We update Table \(\PageIndex{1}\) by placing each expected value in its corresponding core cell, right under the observed value in the cell. This gives the updated table Table \(\PageIndex{2}\).

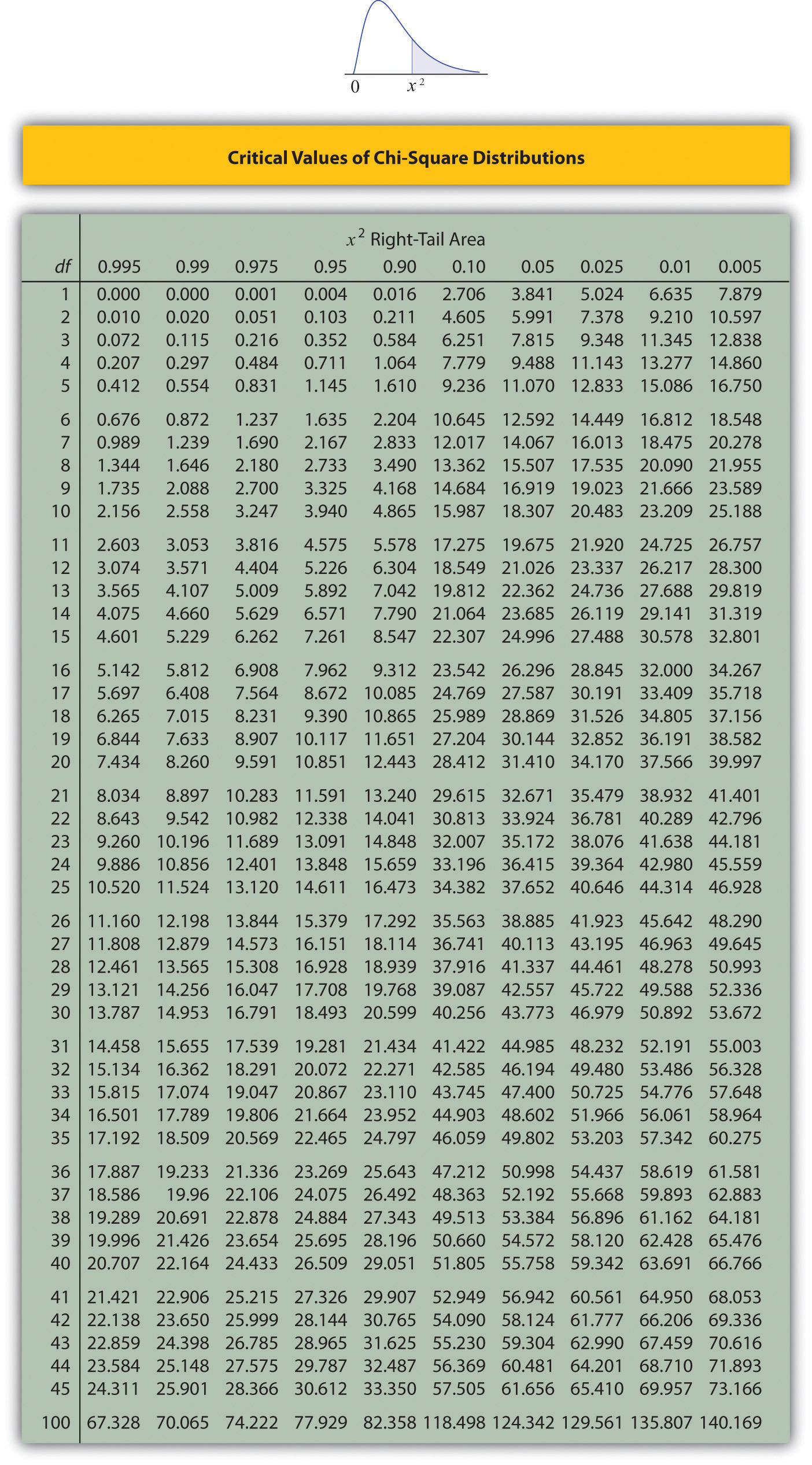
A measure of how much the data deviate from what we would expect to see if the factors really were independent is the sum of the squares of the difference of the numbers in each core cell, or, standardizing by dividing each square by the expected number in the cell, the sum \(\sum (O-E)^2 / E\). We would reject the null hypothesis that the factors are independent only if this number is large, so the test is right-tailed. In this example the random variable \(\sum (O-E)^2 / E\) has the chi-square distribution with one degree of freedom. If we had decided at the outset to test at the \(10\%\) level of significance, the critical value defining the rejection region would be, reading from Figure \(\PageIndex{3}\), \(\chi _{\alpha }^{2}=\chi _{0.10 }^{2}=2.706\), so that the rejection region would be the interval \([2.706,\infty )\). When we compute the value of the standardized test statistic we obtain

\[\sum \frac{(O-E)^2}{E}=\frac{(11-12.6)^2}{12.6}+\frac{(7-5.4)^2}{5.4}+\frac{(17-15.4)^2}{15.4}+\frac{(5-6.6)^2}{6.6}=1.231 \nonumber \]

Since \(1.231 < 2.706\), the decision is not to reject \(H_0\). See Figure \(\PageIndex{4}\). The data do not provide sufficient evidence, at the \(10\%\) level of significance, to conclude that heart rate and gender are related.

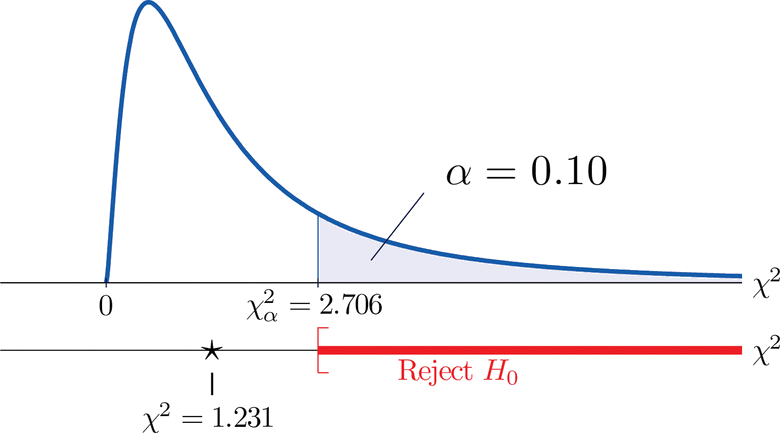
Fig ure \(\PageIndex{4}\) : Baby Gender Prediction

H 0 vs .   H a : : Baby   gender   and   baby   heart   rate   are   independent Baby   gender   and   baby   heart   rate   are   n o t   independent H 0 vs .   H a : : Baby   gender   and   baby   heart   rate   are   independent Baby   gender   and   baby   heart   rate   are   n o t   independent

With this specific example in mind, now turn to the general situation. In the general setting of testing the independence of two factors, call them Factor \(1\) and Factor \(2\), the hypotheses to be tested are

\[H_0: \text{The two factors are independent}\\ vs. \\ H_a: \text{The two factors are not independent} \nonumber \]

As in the example each factor is divided into a number of categories or levels. These could arise naturally, as in the boy-girl division of gender, or somewhat arbitrarily, as in the high-low division of heart rate. Suppose Factor \(1\) has \(I\) levels and Factor \(2\) has \(J\) levels. Then the information from a random sample gives rise to a general \(I\times J\) contingency table, which with row totals, column totals, and a grand total would appear as shown in Table \(\PageIndex{3}\). Each cell may be labeled by a pair of indices \((i,j)\). \(O_{ij}\) stands for the observed count of observations in the cell in row \(i\) and column \(j\), \(R_i\) for the \(i^{th}\) row total and \(C_j\) for the \(j^{th}\) column total. To simplify the notation we will drop the indices so Table \(\PageIndex{3}\) becomes Table \(\PageIndex{4}\). Nevertheless it is important to keep in mind that the \(Os\), the \(Rs\) and the \(Cs\), though denoted by the same symbols, are in fact different numbers.

As in the example, for each core cell in the table we compute what would be the expected number \(E\) of observations if the two factors were independent. \(E\) is computed for each core cell (each cell with an \(O\) in it) of Table \(\PageIndex{4}\) by the rule applied in the example:

\[E=R×Cn \nonumber \]

where \(R\) is the row total and \(C\) is the column total corresponding to the cell, and \(n\) is the sample size

Here is the test statistic for the general hypothesis based on Table \(\PageIndex{5}\), together with the conditions that it follow a chi-square distribution.

Test Statistic for Testing the Independence of Two Factors

\[\chi^2=\sum (O−E)^2E \nonumber \]

where the sum is over all core cells of the table.

• the two study factors are independent, and
• the observed count \(O\) of each cell in Table \(\PageIndex{5}\) is at least \(5\),

then \(\chi ^2\) approximately follows a chi-square distribution with \(df=(I-1)\times (J-1)\) degrees of freedom.

The same five-step procedures, either the critical value approach or the \(p\)-value approach, that were introduced in Section 8.1 and Section 8.3 are used to perform the test, which is always right-tailed.

Example \(\PageIndex{1}\)

A researcher wishes to investigate whether students’ scores on a college entrance examination (\(CEE\)) have any indicative power for future college performance as measured by \(GPA\). In other words, he wishes to investigate whether the factors \(CEE\) and \(GPA\) are independent or not. He randomly selects \(n = 100\) students in a college and notes each student’s score on the entrance examination and his grade point average at the end of the sophomore year. He divides entrance exam scores into two levels and grade point averages into three levels. Sorting the data according to these divisions, he forms the contingency table shown as Table \(\PageIndex{6}\), in which the row and column totals have already been computed.

Test, at the \(1\%\) level of significance, whether these data provide sufficient evidence to conclude that \(CEE\) scores indicate future performance levels of incoming college freshmen as measured by \(GPA\).

We perform the test using the critical value approach, following the usual five-step method outlined at the end of Section 8.1.

• Step 1 . The hypotheses are \[H_0:\text{CEE and GPA are independent factors}\\ vs.\\ H_a:\text{CEE and GPA are not independent factors} \nonumber \]
• Step 2 . The distribution is chi-square.
• 1 st row and 1 st column: \(E=(R\times C)/n=41\times 52/100=21.32\)
• 1 st row and 2 nd column: \(E=(R\times C)/n=36\times 52/100=18.72\)
• 1 st row and 3 rd column: \(E=(R\times C)/n=23\times 52/100=11.96\)
• 2 nd row and 1 st column: \(E=(R\times C)/n=41\times 48/100=19.68\)
• 2 nd row and 2 nd column: \(E=(R\times C)/n=36\times 48/100=17.28\)
• 2 nd row and 3 rd column: \(E=(R\times C)/n=23\times 48/100=11.04\)

Table \(\PageIndex{6}\) is updated to Table \(\PageIndex{6}\).

The test statistic is

\[\begin{align*} \chi^2 &= \sum \frac{(O-E)^2}{E}\\ &= \frac{(35-21.32)^2}{21.32}+\frac{(12-18.72)^2}{18.72}+\frac{(5-11.96)^2}{11.96}+\frac{(6-19.68)^2}{19.68}+\frac{(24-17.28)^2}{17.28}+\frac{(18-11.04)^2}{11.04}\\ &= 31.75 \end{align*} \nonumber \]

• Step 4 . Since the \(CEE\) factor has two levels and the \(GPA\) factor has three, \(I = 2\) and \(J = 3\). Thus the test statistic follows the chi-square distribution with \(df=(2-1)\times (3-1)=2\) degrees of freedom.

Since the test is right-tailed, the critical value is \(\chi _{0.01}^{2}\). Reading from Figure 7.1.6 "Critical Values of Chi-Square Distributions", \(\chi _{0.01}^{2}=9.210\), so the rejection region is \([9.210,\infty )\).

• Step 5 . Since \(31.75 > 9.21\) the decision is to reject the null hypothesis. See Figure \(\PageIndex{5}\). The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that \(CEE\) score and \(GPA\) are not independent: the entrance exam score has predictive power.

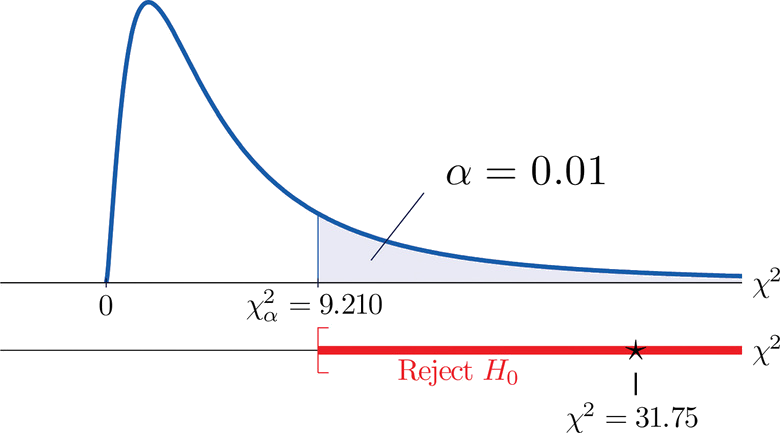
Key Takeaway

• Critical values of a chi-square distribution with degrees of freedom df are found in Figure 7.1.6.
• A chi-square test can be used to evaluate the hypothesis that two random variables or factors are independent.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 12, chi-square statistic for hypothesis testing.

• Chi-square goodness-of-fit example
• Expected counts in a goodness-of-fit test
• Conditions for a goodness-of-fit test
• Test statistic and P-value in a goodness-of-fit test
• Conclusions in a goodness-of-fit test

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

8.1 - the chi-square test of independence.

How do we test the independence of two categorical variables? It will be done using the Chi-Square Test of Independence.

As with all prior statistical tests we need to define null and alternative hypotheses. Also, as we have learned, the null hypothesis is what is assumed to be true until we have evidence to go against it. In this lesson, we are interested in researching if two categorical variables are related or associated (i.e., dependent). Therefore, until we have evidence to suggest that they are, we must assume that they are not. This is the motivation behind the hypothesis for the Chi-Square Test of Independence:

• \(H_0\): In the population, the two categorical variables are independent.
• \(H_a\): In the population, the two categorical variables are dependent.

Note! There are several ways to phrase these hypotheses. Instead of using the words "independent" and "dependent" one could say "there is no relationship between the two categorical variables" versus "there is a relationship between the two categorical variables." Or "there is no association between the two categorical variables" versus "there is an association between the two variables." The important part is that the null hypothesis refers to the two categorical variables not being related while the alternative is trying to show that they are related.

Once we have gathered our data, we summarize the data in the two-way contingency table. This table represents the observed counts and is called the Observed Counts Table or simply the Observed Table. The contingency table on the introduction page to this lesson represented the observed counts of the party affiliation and opinion for those surveyed.

The question becomes, "How would this table look if the two variables were not related?" That is, under the null hypothesis that the two variables are independent, what would we expect our data to look like?

Consider the following table:

The total count is \(A+B+C+D\). Let's focus on one cell, say Group 1 and Success with observed count A. If we go back to our probability lesson, let \(G_1\) denote the event 'Group 1' and \(S\) denote the event 'Success.' Then,

\(P(G_1)=\dfrac{A+B}{A+B+C+D}\) and \(P(S)=\dfrac{A+C}{A+B+C+D}\).

Recall that if two events are independent, then their intersection is the product of their respective probabilities. In other words, if \(G_1\) and \(S\) are independent, then...

\begin{align} P(G_1\cap S)&=P(G_1)P(S)\\&=\left(\dfrac{A+B}{A+B+C+D}\right)\left(\dfrac{A+C}{A+B+C+D}\right)\\[10pt] &=\dfrac{(A+B)(A+C)}{(A+B+C+D)^2}\end{align}

If we considered counts instead of probabilities, then we get the count by multiplying the probability by the total count. In other words...

\begin{align} \text{Expected count for cell with A} &=P(G_1)P(S)\  x\  (\text{total count}) \\   &= \left(\dfrac{(A+B)(A+C)}{(A+B+C+D)^2}\right)(A+B+C+D)\\[10pt]&=\mathbf{\dfrac{(A+B)(A+C)}{A+B+C+D}} \end{align}

This is the count we would expect to see if the two variables were independent (i.e. assuming the null hypothesis is true).

The expected count for each cell under the null hypothesis is:

\(E=\dfrac{\text{(row total)}(\text{column total})}{\text{total sample size}}\)

Example 8-1: Political Affiliation and Opinion Section  

To demonstrate, we will use the Party Affiliation and Opinion on Tax Reform example.

Observed Table:

Find the expected counts for all of the cells.

We need to find what is called the Expected Counts Table or simply the Expected Table. This table displays what the counts would be for our sample data if there were no association between the variables.

Calculating Expected Counts from Observed Counts

Chi-Square Test Statistic Section  

To better understand what these expected counts represent, first recall that the expected counts table is designed to reflect what the sample data counts would be if the two variables were independent. Taking what we know of independent events, we would be saying that the sample counts should show similarity in opinions of tax reform between democrats and republicans. If you find the proportion of each cell by taking a cell's expected count divided by its row total, you will discover that in the expected table each opinion proportion is the same for democrats and republicans. That is, from the expected counts, 0.404 of the democrats and 0.404 of the republicans favor the bill; 0.3 of the democrats and 0.3 of the republicans are indifferent; and 0.296 of the democrats and 0.296 of the republicans are opposed.

The statistical question becomes, "Are the observed counts so different from the expected counts that we can conclude a relationship exists between the two variables?" To conduct this test we compute a Chi-Square test statistic where we compare each cell's observed count to its respective expected count.

In a summary table, we have \(r\times c=rc\) cells. Let \(O_1, O_2, …, O_{rc}\) denote the observed counts for each cell and \(E_1, E_2, …, E_{rc}\) denote the respective expected counts for each cell.

The Chi-Square test statistic is calculated as follows:

\(\chi^{2*}=\frac{(O_1-E_1)^2}{E_1}+\frac{(O_2-E_2)^2}{E_2}+...+\frac{(O_{rc}-E_{rc})^2}{E_{rc}}=\overset{rc}{ \underset{i=1}{\sum}}\frac{(O_i-E_i)^2}{E_i}\)

Under the null hypothesis and certain conditions (discussed below), the test statistic follows a Chi-Square distribution with degrees of freedom equal to \((r-1)(c-1)\), where \(r\) is the number of rows and \(c\) is the number of columns. We leave out the mathematical details to show why this test statistic is used and why it follows a Chi-Square distribution.

As we have done with other statistical tests, we make our decision by either comparing the value of the test statistic to a critical value (rejection region approach) or by finding the probability of getting this test statistic value or one more extreme (p-value approach).

The critical value for our Chi-Square test is \(\chi^2_{\alpha}\) with degree of freedom =\((r - 1) (c -1)\), while the p-value is found by \(P(\chi^2>\chi^{2*})\) with degrees of freedom =\((r - 1)(c - 1)\).

Example 8-1 Cont'd: Chi-Square Section  

Let's apply the Chi-Square Test of Independence to our example where we have a random sample of 500 U.S. adults who are questioned regarding their political affiliation and opinion on a tax reform bill. We will test if the political affiliation and their opinion on a tax reform bill are dependent at a 5% level of significance. Calculate the test statistic.

• Using Minitab

The contingency table ( political_affiliation.csv ) is given below. Each cell contains the observed count and the expected count in parentheses. For example, there were 138 democrats who favored the tax bill. The expected count under the null hypothesis is 115.14. Therefore, the cell is displayed as 138 (115.14).

Calculating the test statistic by hand:

\begin{multline} \chi^{2*}=\dfrac{(138−115.14)^2}{115.14}+\dfrac{(83−85.50)^2}{85.50}+\dfrac{(64−84.36)^2}{84.36}+\\ \dfrac{(64−86.86)^2}{86.86}+\dfrac{(67−64.50)^2}{64.50}+\dfrac{(84−63.64)^2}{63.64}=22.152\end{multline}

...with degrees for freedom equal to \((2 - 1)(3 - 1) = 2\).

  Minitab: Chi-Square Test of Independence

To perform the Chi-Square test in Minitab...

• Choose Stat  >  Tables  >  Chi-Square Test for Association
• If you have summarized data (i.e., observed count) from the drop-down box 'Summarized data in a two-way table.' Select and enter the columns that contain the observed counts, otherwise, if you have the raw data use 'Raw data' (categorical variables). Note that if using the raw data your data will need to consist of two columns: one with the explanatory variable data (goes in the 'row' field) and the response variable data (goes in the 'column' field).
• Labeling (Optional) When using the summarized data you can label the rows and columns if you have the variable labels in columns of the worksheet. For example, if we have a column with the two political party affiliations and a column with the three opinion choices we could use these columns to label the output.
• Click the Statistics  tab. Keep checked the four boxes already checked, but also check the box for 'Each cell's contribution to the chi-square.' Click OK .

Note! If you have the observed counts in a table, you can copy/paste them into Minitab. For instance, you can copy the entire observed counts table (excluding the totals!) for our example and paste these into Minitab starting with the first empty cell of a column.

The following is the Minitab output for this example.

Cell Contents: Count, Expected count, Contribution to Chi-Square

Pearson Chi-Sq = 4.5386 + 0.073 + 4.914 + 6.016 + 0.097 + 6.5137 = 22.152 DF = 2, P-Value = 0.000

Likelihood Ratio Chi-Square

The Chi-Square test statistic is 22.152 and calculated by summing all the individual cell's Chi-Square contributions:

\(4.584 + 0.073 + 4.914 + 6.016 + 0.097 + 6.532 = 22.152\)

The p-value is found by \(P(X^2>22.152)\) with degrees of freedom =\((2-1)(3-1) = 2\).  

Minitab calculates this p-value to be less than 0.001 and reports it as 0.000. Given this p-value of 0.000 is less than the alpha of 0.05, we reject the null hypothesis that political affiliation and their opinion on a tax reform bill are independent. We conclude that there is evidence that the two variables are dependent (i.e., that there is an association between the two variables).

Conditions for Using the Chi-Square Test Section  

Exercise caution when there are small expected counts. Minitab will give a count of the number of cells that have expected frequencies less than five. Some statisticians hesitate to use the Chi-Square test if more than 20% of the cells have expected frequencies below five, especially if the p-value is small and these cells give a large contribution to the total Chi-Square value.

Example 8-2: Tire Quality Section  

The operations manager of a company that manufactures tires wants to determine whether there are any differences in the quality of work among the three daily shifts. She randomly selects 496 tires and carefully inspects them. Each tire is either classified as perfect, satisfactory, or defective, and the shift that produced it is also recorded. The two categorical variables of interest are the shift and condition of the tire produced. The data ( shift_quality.txt ) can be summarized by the accompanying two-way table. Does the data provide sufficient evidence at the 5% significance level to infer that there are differences in quality among the three shifts?

Chi-Square Test

Chi-Sq = 8.647 DF = 4, P-Value = 0.071 

Note that there are 3 cells with expected counts less than 5.0.

In the above example, we don't have a significant result at a 5% significance level since the p-value (0.071) is greater than 0.05. Even if we did have a significant result, we still could not trust the result, because there are 3 (33.3% of) cells with expected counts < 5.0

Sometimes researchers will categorize quantitative data (e.g., take height measurements and categorize as 'below average,' 'average,' and 'above average.') Doing so results in a loss of information - one cannot do the reverse of taking the categories and reproducing the raw quantitative measurements. Instead of categorizing, the data should be analyzed using quantitative methods.

Try it! Section  

A food services manager for a baseball park wants to know if there is a relationship between gender (male or female) and the preferred condiment on a hot dog. The following table summarizes the results. Test the hypothesis with a significance level of 10%.

The hypotheses are:

• \(H_0\): Gender and condiments are independent
• \(H_a\): Gender and condiments are not independent

We need to expected counts table:

None of the expected counts in the table are less than 5. Therefore, we can proceed with the Chi-Square test.

The test statistic is:

\(\chi^{2*}=\frac{(15-19.2)^2}{19.2}+\frac{(23-20.16)^2}{20.16}+...+\frac{(8-9.36)^2}{9.36}=2.95\)

The p-value is found by \(P(\chi^2>\chi^{2*})=P(\chi^2>2.95)\) with (3-1)(2-1)=2 degrees of freedom. Using a table or software, we find the p-value to be 0.2288.

With a p-value greater than 10%, we can conclude that there is not enough evidence in the data to suggest that gender and preferred condiment are related.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability, a comprehensive look at percentile in statistics, the best guide to understand bayes theorem, everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test.

A Complete Guide on Hypothesis Testing in Statistics

Understanding the Fundamentals of Arithmetic and Geometric Progression

The definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution, all you need to know about bias in statistics, a complete guide to get a grasp of time series analysis.

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is a chi-square test formula, examples & application.

Lesson 9 of 24 By Avijeet Biswal

Table of Contents

The world is constantly curious about the Chi-Square test's application in machine learning and how it makes a difference. Feature selection is a critical topic in machine learning , as you will have multiple features in line and must choose the best ones to build the model. By examining the relationship between the elements, the chi-square test aids in the solution of feature selection problems. In this tutorial, you will learn about the chi-square test and its application.

What Is a Chi-Square Test?

The Chi-Square test is a statistical procedure for determining the difference between observed and expected data. This test can also be used to determine whether it correlates to the categorical variables in our data. It helps to find out whether a difference between two categorical variables is due to chance or a relationship between them.

Chi-Square Test Definition

A chi-square test is a statistical test that is used to compare observed and expected results. The goal of this test is to identify whether a disparity between actual and predicted data is due to chance or to a link between the variables under consideration. As a result, the chi-square test is an ideal choice for aiding in our understanding and interpretation of the connection between our two categorical variables.

A chi-square test or comparable nonparametric test is required to test a hypothesis regarding the distribution of a categorical variable. Categorical variables, which indicate categories such as animals or countries, can be nominal or ordinal. They cannot have a normal distribution since they can only have a few particular values.

For example, a meal delivery firm in India wants to investigate the link between gender, geography, and people's food preferences.

It is used to calculate the difference between two categorical variables, which are:

• As a result of chance or
• Because of the relationship

Your Data Analytics Career is Around The Corner!

Formula For Chi-Square Test

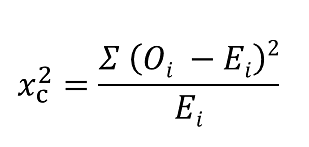
c = Degrees of freedom

O = Observed Value

E = Expected Value

The degrees of freedom in a statistical calculation represent the number of variables that can vary in a calculation. The degrees of freedom can be calculated to ensure that chi-square tests are statistically valid. These tests are frequently used to compare observed data with data that would be expected to be obtained if a particular hypothesis were true.

The Observed values are those you gather yourselves.

The expected values are the frequencies expected, based on the null hypothesis. 

Fundamentals of Hypothesis Testing

Hypothesis testing is a technique for interpreting and drawing inferences about a population based on sample data. It aids in determining which sample data best support mutually exclusive population claims.

Null Hypothesis (H0) - The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

Alternate Hypothesis(H1 or Ha) - The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Become a Data Science Expert & Get Your Dream Job

What Are Categorical Variables?

Categorical variables belong to a subset of variables that can be divided into discrete categories. Names or labels are the most common categories. These variables are also known as qualitative variables because they depict the variable's quality or characteristics.

Categorical variables can be divided into two categories:

• Nominal Variable: A nominal variable's categories have no natural ordering. Example: Gender, Blood groups
• Ordinal Variable: A variable that allows the categories to be sorted is ordinal variables. Customer satisfaction (Excellent, Very Good, Good, Average, Bad, and so on) is an example.

Why Do You Use the Chi-Square Test?

Chi-square is a statistical test that examines the differences between categorical variables from a random sample in order to determine whether the expected and observed results are well-fitting.

Here are some of the uses of the Chi-Squared test:

• The Chi-squared test can be used to see if your data follows a well-known theoretical probability distribution like the Normal or Poisson distribution.
• The Chi-squared test allows you to assess your trained regression model's goodness of fit on the training, validation, and test data sets.

Become an Expert in Data Analytics!

What Does A Chi-Square Statistic Test Tell You?

A Chi-Square test ( symbolically represented as  2 ) is fundamentally a data analysis based on the observations of a random set of variables. It computes how a model equates to actual observed data. A Chi-Square statistic test is calculated based on the data, which must be raw, random, drawn from independent variables, drawn from a wide-ranging sample and mutually exclusive. In simple terms, two sets of statistical data are compared -for instance, the results of tossing a fair coin. Karl Pearson introduced this test in 1900 for categorical data analysis and distribution. This test is also known as ‘Pearson’s Chi-Squared Test’. 

Chi-Squared Tests are most commonly used in hypothesis testing. A hypothesis is an assumption that any given condition might be true, which can be tested afterwards. The Chi-Square test estimates the size of inconsistency between the expected results and the actual results when the size of the sample and the number of variables in the relationship is mentioned. 

These tests use degrees of freedom to determine if a particular null hypothesis can be rejected based on the total number of observations made in the experiments. Larger the sample size, more reliable is the result.

There are two main types of Chi-Square tests namely -

Independence 

• Goodness-of-Fit 

The Chi-Square Test of Independence is a derivable ( also known as inferential ) statistical test which examines whether the two sets of variables are likely to be related with each other or not. This test is used when we have counts of values for two nominal or categorical variables and is considered as non-parametric test. A relatively large sample size and independence of obseravations are the required criteria for conducting this test.

For Example- 

In a movie theatre, suppose we made a list of movie genres. Let us consider this as the first variable. The second variable is whether or not the people who came to watch those genres of movies have bought snacks at the theatre. Here the null hypothesis is that th genre of the film and whether people bought snacks or not are unrelatable. If this is true, the movie genres don’t impact snack sales. 

Future-Proof Your AI/ML Career: Top Dos and Don'ts

Goodness-Of-Fit

In statistical hypothesis testing, the Chi-Square Goodness-of-Fit test determines whether a variable is likely to come from a given distribution or not. We must have a set of data values and the idea of the distribution of this data. We can use this test when we have value counts for categorical variables. This test demonstrates a way of deciding if the data values have a “ good enough” fit for our idea or if it is a representative sample data of the entire population. 

Suppose we have bags of balls with five different colours in each bag. The given condition is that the bag should contain an equal number of balls of each colour. The idea we would like to test here is that the proportions of the five colours of balls in each bag must be exact. 

Who Uses Chi-Square Analysis?

Chi-square is most commonly used by researchers who are studying survey response data because it applies to categorical variables. Demography, consumer and marketing research, political science, and economics are all examples of this type of research.

Let's say you want to know if gender has anything to do with political party preference. You poll 440 voters in a simple random sample to find out which political party they prefer. The results of the survey are shown in the table below:

To see if gender is linked to political party preference, perform a Chi-Square test of independence using the steps below.

Step 1: Define the Hypothesis

H0: There is no link between gender and political party preference.

H1: There is a link between gender and political party preference.

Step 2: Calculate the Expected Values

Now you will calculate the expected frequency.

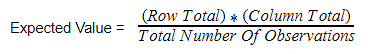
For example, the expected value for Male Republicans is: 

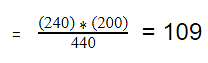
Similarly, you can calculate the expected value for each of the cells.

Step 3: Calculate (O-E)2 / E for Each Cell in the Table

Now you will calculate the (O - E)2 / E for each cell in the table.

Step 4: Calculate the Test Statistic X2

X2  is the sum of all the values in the last table

 =  0.743 + 2.05 + 2.33 + 3.33 + 0.384 + 1

Before you can conclude, you must first determine the critical statistic, which requires determining our degrees of freedom. The degrees of freedom in this case are equal to the table's number of columns minus one multiplied by the table's number of rows minus one, or (r-1) (c-1). We have (3-1)(2-1) = 2.

Finally, you compare our obtained statistic to the critical statistic found in the chi-square table. As you can see, for an alpha level of 0.05 and two degrees of freedom, the critical statistic is 5.991, which is less than our obtained statistic of 9.83. You can reject our null hypothesis because the critical statistic is higher than your obtained statistic.

This means you have sufficient evidence to say that there is an association between gender and political party preference.

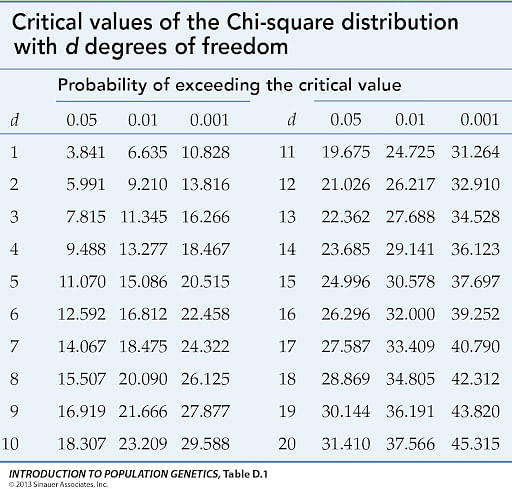
When to Use a Chi-Square Test?

A Chi-Square Test is used to examine whether the observed results are in order with the expected values. When the data to be analysed is from a random sample, and when the variable is the question is a categorical variable, then Chi-Square proves the most appropriate test for the same. A categorical variable consists of selections such as breeds of dogs, types of cars, genres of movies, educational attainment, male v/s female etc. Survey responses and questionnaires are the primary sources of these types of data. The Chi-square test is most commonly used for analysing this kind of data. This type of analysis is helpful for researchers who are studying survey response data. The research can range from customer and marketing research to political sciences and economics. 

The Ultimate Ticket to Top Data Science Job Roles

Chi-Square Distribution 

Chi-square distributions (X2) are a type of continuous probability distribution. They're commonly utilized in hypothesis testing, such as the chi-square goodness of fit and independence tests. The parameter k, which represents the degrees of freedom, determines the shape of a chi-square distribution.

A chi-square distribution is followed by very few real-world observations. The objective of chi-square distributions is to test hypotheses, not to describe real-world distributions. In contrast, most other commonly used distributions, such as normal and Poisson distributions, may explain important things like baby birth weights or illness cases per year.

Because of its close resemblance to the conventional normal distribution, chi-square distributions are excellent for hypothesis testing. Many essential statistical tests rely on the conventional normal distribution.

In statistical analysis , the Chi-Square distribution is used in many hypothesis tests and is determined by the parameter k degree of freedoms. It belongs to the family of continuous probability distributions . The Sum of the squares of the k independent standard random variables is called the Chi-Squared distribution. Pearson’s Chi-Square Test formula is - 

Where X^2 is the Chi-Square test symbol

Σ is the summation of observations

O is the observed results

E is the expected results 

The shape of the distribution graph changes with the increase in the value of k, i.e. degree of freedoms. 

When k is 1 or 2, the Chi-square distribution curve is shaped like a backwards ‘J’. It means there is a high chance that X^2 becomes close to zero. 

Courtesy: Scribbr

When k is greater than 2, the shape of the distribution curve looks like a hump and has a low probability that X^2 is very near to 0 or very far from 0. The distribution occurs much longer on the right-hand side and shorter on the left-hand side. The probable value of X^2 is (X^2 - 2).

When k is greater than ninety, a normal distribution is seen, approximating the Chi-square distribution.

Become a Data Scientist With Real-World Experience

Chi-Square P-Values

Here P denotes the probability; hence for the calculation of p-values, the Chi-Square test comes into the picture. The different p-values indicate different types of hypothesis interpretations. 

• P <= 0.05 (Hypothesis interpretations are rejected)
• P>= 0.05 (Hypothesis interpretations are accepted) 

The concepts of probability and statistics are entangled with Chi-Square Test. Probability is the estimation of something that is most likely to happen. Simply put, it is the possibility of an event or outcome of the sample. Probability can understandably represent bulky or complicated data. And statistics involves collecting and organising, analysing, interpreting and presenting the data. 

Finding P-Value

When you run all of the Chi-square tests, you'll get a test statistic called X2. You have two options for determining whether this test statistic is statistically significant at some alpha level:

• Compare the test statistic X2 to a critical value from the Chi-square distribution table.
• Compare the p-value of the test statistic X2 to a chosen alpha level.

Test statistics are calculated by taking into account the sampling distribution of the test statistic under the null hypothesis, the sample data, and the approach which is chosen for performing the test. 

The p-value will be as mentioned in the following cases.

• A lower-tailed test is specified by: P(TS ts | H0 is true) p-value = cdf (ts)
• Lower-tailed tests have the following definition: P(TS ts | H0 is true) p-value = cdf (ts)
• A two-sided test is defined as follows, if we assume that the test static distribution  of H0 is symmetric about 0. 2 * P(TS |ts| | H0 is true) = 2 * (1 - cdf(|ts|))

P: probability Event

TS: Test statistic is computed observed value of the test statistic from your sample cdf(): Cumulative distribution function of the test statistic's distribution (TS)

Types of Chi-square Tests

Pearson's chi-square tests are classified into two types:

• Chi-square goodness-of-fit analysis
• Chi-square independence test

These are, mathematically, the same exam. However, because they are utilized for distinct goals, we generally conceive of them as separate tests.

The chi-square test has the following significant properties:

• If you multiply the number of degrees of freedom by two, you will receive an answer that is equal to the variance.
• The chi-square distribution curve approaches the data is normally distributed as the degree of freedom increases.
• The mean distribution is equal to the number of degrees of freedom.

Properties of Chi-Square Test 

• Variance is double the times the number of degrees of freedom.
• Mean distribution is equal to the number of degrees of freedom.
• When the degree of freedom increases, the Chi-Square distribution curve becomes normal.

Limitations of Chi-Square Test

There are two limitations to using the chi-square test that you should be aware of. 

• The chi-square test, for starters, is extremely sensitive to sample size. Even insignificant relationships can appear statistically significant when a large enough sample is used. Keep in mind that "statistically significant" does not always imply "meaningful" when using the chi-square test.
• Be mindful that the chi-square can only determine whether two variables are related. It does not necessarily follow that one variable has a causal relationship with the other. It would require a more detailed analysis to establish causality.

Get In-Demand Skills to Launch Your Data Career

Chi-Square Goodness of Fit Test

When there is only one categorical variable, the chi-square goodness of fit test can be used. The frequency distribution of the categorical variable is evaluated for determining whether it differs significantly from what you expected. The idea is that the categories will have equal proportions, however, this is not always the case.

When you want to see if there is a link between two categorical variables, you perform the chi-square test. To acquire the test statistic and its related p-value in SPSS, use the chisq option on the statistics subcommand of the crosstabs command. Remember that the chi-square test implies that each cell's anticipated value is five or greater.

In this tutorial titled ‘The Complete Guide to Chi-square test’, you explored the concept of Chi-square distribution and how to find the related values. You also take a look at how the critical value and chi-square value is related to each other.

If you want to gain more insight and get a work-ready understanding in statistical concepts and learn how to use them to get into a career in Data Analytics , our Post Graduate Program in Data Analytics in partnership with Purdue University should be your next stop. A comprehensive program with training from top practitioners and in collaboration with IBM, this will be all that you need to kickstart your career in the field. 

Was this tutorial on the Chi-square test useful to you? Do you have any doubts or questions for us? Mention them in this article's comments section, and we'll have our experts answer them for you at the earliest!

1) What is the chi-square test used for? 

The chi-square test is a statistical method used to determine if there is a significant association between two categorical variables. It helps researchers understand whether the observed distribution of data differs from the expected distribution, allowing them to assess whether any relationship exists between the variables being studied.

2) What is the chi-square test and its types? 

The chi-square test is a statistical test used to analyze categorical data and assess the independence or association between variables. There are two main types of chi-square tests: a) Chi-square test of independence: This test determines whether there is a significant association between two categorical variables. b) Chi-square goodness-of-fit test: This test compares the observed data to the expected data to assess how well the observed data fit the expected distribution.

3) What is the chi-square test easily explained? 

The chi-square test is a statistical tool used to check if two categorical variables are related or independent. It helps us understand if the observed data differs significantly from the expected data. By comparing the two datasets, we can draw conclusions about whether the variables have a meaningful association.

4) What is the difference between t-test and chi-square? 

The t-test and the chi-square test are two different statistical tests used for different types of data. The t-test is used to compare the means of two groups and is suitable for continuous numerical data. On the other hand, the chi-square test is used to examine the association between two categorical variables. It is applicable to discrete, categorical data. So, the choice between the t-test and chi-square test depends on the nature of the data being analyzed.

5) What are the characteristics of chi-square? 

The chi-square test has several key characteristics:

1) It is non-parametric, meaning it does not assume a specific probability distribution for the data.

2) It is sensitive to sample size; larger samples can result in more significant outcomes.

3) It works with categorical data and is used for hypothesis testing and analyzing associations.

4) The test output provides a p-value, which indicates the level of significance for the observed relationship between variables.

5)It can be used with different levels of significance (e.g., 0.05 or 0.01) to determine statistical significance.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Getting Started with Google Display Network: The Ultimate Beginner’s Guide

Sanity Testing Vs Smoke Testing: Know the Differences, Applications, and Benefits Of Each

Fundamentals of Software Testing

The Building Blocks of API Development

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

8. The Chi squared tests

The χ²tests.

χ 2  = ∑(O i – E i ) 2 /E i

where O i is the observed value and E i is the expected value.

Chi-Square Test of Independence

The chi-square test of independence also known as the chi-square test of association which is used to determine the association between the categorical variables. It is considered as a non-parametric test . It is mostly used to test statistical independence.

The chi-square test of independence is not appropriate when the categorical variables represent the pre-test and post-test observations. For this test, the data must meet the following requirements:

• Two categorical variables
• Relatively large sample size
• Categories of variables (two or more)
• Independence of observations

Example of Categorical Data

Let us take an example of a categorical data where there is a society of 1000 residents with four neighbourhoods, P, Q, R and S. A random sample of 650 residents of the society is taken whose occupations are doctors, engineers and teachers. The null hypothesis is that each person’s neighbourhood of residency is independent of the person’s professional division. The data are categorised as:

Assume the sample living in neighbourhood P, 150, to estimate what proportion of the whole 1,000 people live in neighbourhood P. In the same way, we take 349/650 to calculate what ratio of the 1,000 are doctors. By the supposition of independence under the hypothesis, we should “expect” the number of doctors in neighbourhood P is;

150 x 349/650  ≈ 80.54

So by  the chi-square test formula for that particular cell in the table, we get;

(Observed – Expected) 2 /Expected Value = (90-80.54) 2 /80.54  ≈ 1.11

Some of the exciting facts about the Chi-square test are given below:

The Chi-square statistic can only be used on numbers. We cannot use them for data in terms of percentages, proportions, means or similar statistical contents. Suppose, if we have 20% of 400 people, we need to convert it to a number, i.e. 80, before running a test statistic.

A chi-square test will give us a p-value. The p-value will tell us whether our test results are significant or not. 

However, to perform a chi-square test and get the p-value, we require two pieces of information:

(1) Degrees of freedom. That’s just the number of categories minus 1.

(2) The alpha level(α). You or the researcher chooses this. The usual alpha level is 0.05 (5%), but you could also have other levels like 0.01 or 0.10.

In elementary statistics, we usually get questions along with the degrees of freedom(DF) and the alpha level. Thus, we don’t usually have to figure out what they are. To get the degrees of freedom, count the categories and subtract 1.

The chi-square distribution table with three probability levels is provided here. The statistic here is used to examine whether distributions of certain variables vary from one another. The categorical variable will produce data in the categories and numerical variables will produce data in numerical form.

The distribution of χ 2 with (r-1)(c-1) degrees of freedom(DF) , is represented in the table given below. Here, r represents the number of rows in the two-way table and c represents the number of columns.

Solved Problem

 A survey on cars had conducted in 2011 and determined that 60% of car owners have  only one car, 28% have two cars, and 12% have three or more. Supposing that you have decided to conduct your own survey and have collected the data below, determine whether your data supports the results of the study.

Use a significance level of 0.05. Also, given that, out of 129 car owners, 73 had one car and 38 had two cars.

Let us state the null and alternative hypotheses.

H 0 : The proportion of car owners with one, two or three cars is 0.60, 0.28 and 0.12 respectively.

H 1 : The proportion of car owners with one, two or three cars does not match the proposed model.

A Chi-Square goodness of fit test is appropriate because we are examining the distribution of a single categorical variable. 

Let’s tabulate the given information and calculate the required values.

Therefore, χ 2  = ∑(O i  – E i ) 2 /E i  = 0.7533

Let’s compare it to the chi-square value for the significance level 0.05. 

The degrees for freedom = 3 – 1 = 2

Using the table, the critical value for a 0.05 significance level with df = 2 is 5.99. 

That means that 95 times out of 100, a survey that agrees with a sample will have a χ 2  value of 5.99 or less. 

The Chi-square statistic is only 0.7533, so we will accept the null hypothesis.

Frequently Asked Questions – FAQs

What is the chi-square test write its formula, how do you calculate chi squared, what is a chi-square test used for, how do you interpret a chi-square test, what is a good chi-square value, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Statistics Made Easy

Chi-Square Test of Independence: Definition, Formula, and Example

A Chi-Square Test of Independence  is used to determine whether or not there is a significant association between two categorical variables.

This tutorial explains the following:

• The motivation for performing a Chi-Square Test of Independence.
• The formula to perform a Chi-Square Test of Independence.
• An example of how to perform a Chi-Square Test of Independence.

Chi-Square Test of Independence: Motivation

A Chi-Square test of independence can be used to determine if there is an association between two categorical variables in a many different settings. Here are a few examples:

• We want to know if gender is associated with political party preference so we survey 500 voters and record their gender and political party preference.
• We want to know if a person’s favorite color is associated with their favorite sport so we survey 100 people and ask them about their preferences for both.
• We want to know if education level and marital status are associated so we collect data about these two variables on a simple random sample of 50 people.

In each of these scenarios we want to know if two categorical variables are associated with each other. In each scenario, we can use a Chi-Square test of independence to determine if there is a statistically significant association between the variables. 

Chi-Square Test of Independence: Formula

A Chi-Square test of independence uses the following null and alternative hypotheses:

• H 0 : (null hypothesis)  The two variables are independent.
• H 1 : (alternative hypothesis)  The two variables are not independent. (i.e. they are associated)

We use the following formula to calculate the Chi-Square test statistic X 2 :

X 2 = Σ(O-E) 2  / E

• Σ:  is a fancy symbol that means “sum”
• O:  observed value
• E:  expected value

If the p-value that corresponds to the test statistic X 2  with (#rows-1)*(#columns-1) degrees of freedom is less than your chosen significance level then you can reject the null hypothesis.

Chi-Square Test of Independence: Example

Suppose we want to know whether or not gender is associated with political party preference. We take a simple random sample of 500 voters and survey them on their political party preference. The following table shows the results of the survey:

Use the following steps to perform a Chi-Square test of independence to determine if gender is associated with political party preference.

Step 1: Define the hypotheses.

We will perform the Chi-Square test of independence using the following hypotheses:

• H 0 :  Gender and political party preference are independent.
• H 1 : Gender and political party preference are  not independent.

Step 2: Calculate the expected values.

Next, we will calculate the expected values for each cell in the contingency table using the following formula:

Expected value = (row sum * column sum) / table sum.

For example, the expected value for Male Republicans is: (230*250) / 500 =  115 .

We can repeat this formula to obtain the expected value for each cell in the table:

Step 3: Calculate (O-E) 2  / E for each cell in the table.

Next we will calculate  (O-E) 2  / E  for each cell in the table  where:

For example, Male Republicans would have a value of: (120-115) 2 /115 =  0.2174 .

We can repeat this formula for each cell in the table:

Step 4: Calculate the test statistic X 2  and the corresponding p-value.

X 2  = Σ(O-E) 2  / E = 0.2174 + 0.2174 + 0.0676 + 0.0676 + 0.1471 + 0.1471 =  0.8642

According to the Chi-Square Score to P Value Calculator , the p-value associated with X 2  = 0.8642 and (2-1)*(3-1) = 2 degrees of freedom is  0.649198 .

Step 5: Draw a conclusion.

Since this p-value is not less than 0.05, we fail to reject the null hypothesis. This means we do not have sufficient evidence to say that there is an association between gender and political party preference.

Note:  You can also perform this entire test by simply using the Chi-Square Test of Independence Calculator .

Additional Resources

The following tutorials explain how to perform a Chi-Square test of independence using different statistical programs:

How to Perform a Chi-Square Test of Independence in Stata How to Perform a Chi-Square Test of Independence in Excel How to Perform a Chi-Square Test of Independence in SPSS How to Perform a Chi-Square Test of Independence in Python How to Perform a Chi-Square Test of Independence in R Chi-Square Test of Independence on a TI-84 Calculator Chi-Square Test of Independence Calculator

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

One Reply to “Chi-Square Test of Independence: Definition, Formula, and Example”

what test do I use if there are 2 categorical variables and one categorical DV? as in I want to test political attitudes and beliefs in conspiracies and how they affect Covid conspiracy thinking

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Teach yourself statistics

Chi-Square Test of Homogeneity

This lesson explains how to conduct a chi-square test of homogeneity . The test is applied to a single categorical variable from two or more different populations. It is used to determine whether frequency counts are distributed identically across different populations.

For example, in a survey of TV viewing preferences, we might ask respondents to identify their favorite program. We might ask the same question of two different populations, such as males and females. We could use a chi-square test for homogeneity to determine whether male viewing preferences differed significantly from female viewing preferences. The sample problem at the end of the lesson considers this example.

When to Use Chi-Square Test for Homogeneity

The test procedure described in this lesson is appropriate when the following conditions are met:

• For each population, the sampling method is simple random sampling .
• The variable under study is categorical .
• If sample data are displayed in a contingency table (Populations x Category levels), the expected frequency count for each cell of the table is at least 5.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

Suppose that data were sampled from r populations, and assume that the categorical variable had c levels. At any specified level of the categorical variable, the null hypothesis states that each population has the same proportion of observations. Thus,

The alternative hypothesis (H a ) is that at least one of the null hypothesis statements is false.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the chi-square test for homogeneity to determine whether observed sample frequencies differ significantly from expected frequencies specified in the null hypothesis. The chi-square test for homogeneity is described in the next section.

Analyze Sample Data

Using sample data from the contingency tables, find the degrees of freedom, expected frequency counts, test statistic, and the P-value associated with the test statistic. The analysis described in this section is illustrated in the sample problem at the end of this lesson.

DF = (r - 1) * (c - 1)

E r,c = (n r * n c ) / n

Χ 2 = Σ [ (O r,c - E r,c ) 2 / E r,c ]

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a chi-square, use the Chi-Square Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In a study of the television viewing habits of children, a developmental psychologist selects a random sample of 300 first graders - 100 boys and 200 girls. Each child is asked which of the following TV programs they like best: The Lone Ranger, Sesame Street, or The Simpsons. Results are shown in the contingency table below.

Do the boys' preferences for these TV programs differ significantly from the girls' preferences? Use a 0.05 level of significance.

The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.

• Alternative hypothesis: At least one of the null hypothesis statements is false.
• Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a chi-square test for homogeneity .

DF = (r - 1) * (c - 1) DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2

E r,c = (n r * n c ) / n E 1,1 = (100 * 100) / 300 = 10000/300 = 33.3 E 1,2 = (100 * 110) / 300 = 11000/300 = 36.7 E 1,3 = (100 * 90) / 300 = 9000/300 = 30.0 E 2,1 = (200 * 100) / 300 = 20000/300 = 66.7 E 2,2 = (200 * 110) / 300 = 22000/300 = 73.3 E 2,3 = (200 * 90) / 300 = 18000/300 = 60.0

Χ 2 = Σ[ (O r,c - E r,c ) 2 / E r,c ] Χ 2 = (50 - 33.3) 2 /33.3 + (30 - 36.7) 2 /36.7 + (20 - 30) 2 /30 + (50 - 66.7) 2 /66.7 + (80 - 73.3) 2 /73.3 + (70 - 60) 2 /60 Χ 2 = (16.7) 2 /33.3 + (-6.7) 2 /36.7 + (-10.0) 2 /30 + (-16.7) 2 /66.7 + (3.3) 2 /73.3 + (10) 2 /60 Χ 2 = 8.38 + 1.22 + 3.33 + 4.18 + 0.61 + 1.67 = 19.39

where DF is the degrees of freedom, r is the number of populations, c is the number of levels of the categorical variable, n r is the number of observations from population r , n c is the number of observations from level c of the categorical variable, n is the number of observations in the sample, E r,c is the expected frequency count in population r for level c , and O r,c is the observed frequency count in population r for level c .

The P-value is the probability that a chi-square statistic having 2 degrees of freedom is more extreme than 19.39. We use the Chi-Square Distribution Calculator to find P(Χ 2 > 19.39) = 0.00006.

• Interpret results . Since the P-value (0.00006) is less than the significance level (0.05), we reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the variable under study was categorical, and the expected frequency count was at least 5 in each population at each level of the categorical variable.

• Study Guides
• Homework Questions

Packet 6 - Chi-Square Test for Independence (2)