ratio problem solving and reasoning

6th Grade Games - Understand ratio concepts and use ratio reasoning to solve problems.

Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, "The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak." "For every vote candidate A received, candidate C received nearly three votes."

Understand the concept of a unit rate a/b associated with a ratio a:b with b not equal to 0, and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar." "We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.

Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.

• Make tables of equivalent ratios relating quantities with wholenumber measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.
• Solve unit rate problems including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?
• Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.
• Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.

Connect with Us

Rate and keep track of your favorite activities! Sign Up to Rate Activities!

Create an Account!

Please pick a grade, elementary school math games, middle school math games, elementary school videos, middle school videos, elementary school worksheets, middle school worksheets, elementary school activities, middle school activities.

Understand ratio concepts and use ratio reasoning to solve problems.

More specific topics in understand ratio concepts and use ratio reasoning to solve problems..

• Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
• Understand the concept of a unit rate a/b associated with a ratio a:b with b ? 0, and use rate language in the context of a ratio relationship.

Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.

• Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.
• Solve unit rate problems including those involving unit pricing and constant speed.
• Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.
• Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.

Popular Tutorials in Understand ratio concepts and use ratio reasoning to solve problems.

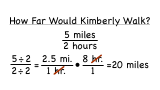
How Do You Solve a Word Problem Using Unit Rates?

Word problems allow you to see the real world uses of math! This tutorial shows you how to take a rate and convert it to a unit rate. Then, you can use that unit rate to calculate your answer. Watch this tutorial to learn all about it!

How Do You Convert a Rate To A Unit Rate?

When you talk about the speed of a car, you usually say something in miles per hour. For example, you say, 'I drove 40 miles per hour.' Normally, you don't say, 'I drove 120 miles per 3 hours.' Figure out how to convert a rate like 120 miles per 3 hours to the unit rate of 40 miles per hour by watching this tutorial.

What are Rates and Unit Rates?

Can you do 100 sit-ups in 2 minutes? That's a rate! Driving a car going 40 miles per hour? That's a unit rate! Watch this tutorial to learn about rate and unit rate (and the difference!).

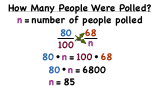
How Do You Solve a Word Problem Using a Percent Proportion?

Word problems allow you to see the real world uses of math! This tutorial shows you how to take a words problem and turn it into a percent proportion. Then see how to solve for the answer using the mean extremes property of proportions. Take a look!

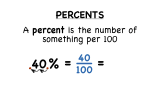
What's a Percent?

Sales tax, tips at restaurants, grades on tests... no matter what you do, you can't run away from percents. So watch this tutorial and see once and for all what percents are all about!

How Do You Turn a Percent into a Decimal?

Percents and Decimals are just tools that let us represent numbers, and that is why percents can be converted into decimals, and decimals can be converted into percents. In this tutorial you'll see how quickly you can convert percents into decimals!

How Do You Set Up a Percent Proportion from a Word Problem?

Sometimes the hardest part of a word problem is figuring out how to turn the words into an equation you can solve. This tutorial let's you see the steps to take in order to do just that! Take a look! You'll be glad you did!

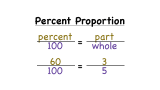
What's a Percent Proportion?

Percents are important, and the reality is that percents are actually proportions in disguise. In this tutorial you'll see exactly how to connect percents with proportions, and you'll be happier for it :)

What's a Ratio?

Ratios are everywhere! The scale on a map or blueprint is a ratio. Ingredients sometimes need to be mixed using ratios such as the ratio of water to cement mix when making cement. Watch this tutorial to learn about ratios. Then think of some ratios you've encountered before!

How Do You Convert Cups to Pints?

It can be helpful to see a capacity given in different units. This tutorial shows you how to take a measurement in cups and convert it to pints!

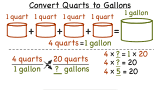
How Do You Convert Quarts to Gallons?

If you go to the store to buy a certain number of quarts of milk and the store only sells milk in gallons, what do you do? You need to convert those quarts into gallons! Follow along with this tutorial to learn how.

How Do You Find Equivalent Ratios by Making a Table?

To master equivalent ratios, you need to practice. Follow along with this tutorial to practice filling in a table with equivalent ratios.

How Do You Use a Table of Equivalent Ratios to Predict a Value?

Patterns are everywhere! In this tutorial, you'll see how to use the pattern in a table to find an answer to a word problem.

How Do You Write Ratios From a Table?

This tutorial goes through the steps of creating ratios from a table of values! Follow along to see how the ratios are made!

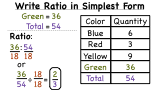
How Do You Write a Ratio in Simplest Form?

In this tutorial, you'll see how to take the information from a given table and use it to find a ratio. You'll also see how to write the answer in simplest form!

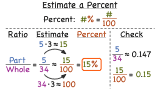
How Do You Estimate a Percent?

When something is on sale, it's good to know how much you're saving! This tutorial shows you how to estimate a percent using an original price and a coupon!

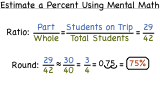
How Do You Use Mental Math to Estimate a Percent?

Mental math is a powerful tool! See how to use mental math in this tutorial to estimate a percent!

How Do You Find Equivalent Ratios?

Ratios are used to compare numbers. When you're working with ratios, it's sometimes easier to work with an equivalent ratio. Equivalent ratios have different numbers but represent the same relationship. In this tutorial, you'll see how to find equivalent ratios by first writing the given ratio as a fraction. Take a look!

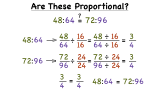
How Do You Know If Two Ratios are Proportional?

Ratios are proportional if they represent the same relationship. One way to see if two ratios are proportional is to write them as fractions and then reduce them. If the reduced fractions are the same, your ratios are proportional. To see this process in action, check out this tutorial!

How Do You Write a Ratio From a Word Problem?

Sometimes the hardest part of a word problem is figuring out how to turn the words into a math problem. In this tutorial, you'll see how to take the information given in a word problem and write a ratio. Then, reduce the ratio and explain its meaning. See it all in this tutorial!

How Do You Use Unit Rates to Compare Rates?

Word problems allow you to see the real world uses of math! This tutorial shows you how to use ratios to figure out which store has a better deal on cupcakes. Take a look!

How Do You Use Dimensional Analysis to Convert Units on One Part of a Rate?

Word problems are a great way to see math in action! In this tutorial, learn how to use the information given in a word problem to create a rate. Then, find and use a conversion factor to convert a unit in the rate. Take a look!

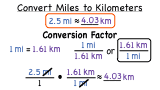
How Do You Convert Miles to Kilometers?

The world is full of different units of measure, and it's important to know how to convert from one unit to another. This tutorial shows you how to convert from miles to kilometers. Check it out!

How Do You Convert Yards to Meters?

What are Equivalent Ratios?

Equivalent ratios are just like equivalent fractions. If two ratios have the same value, then they are equivalent, even though they may look very different! In this tutorial, take a look at equivalent ratios and learn how to tell if you have equivalent ratios.

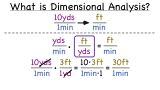
What is Dimensional, or Unit Analysis?

If you’re solving a math problem or word problem that contains units, you need to remember to include your units in your answer. By using dimensional analysis or unit analysis, you can include those units as you solve! Watch this tutorial and take a look at dimensional analysis!

How Do You Put Fractions, Decimals, and Percents in Order?

Ordering numbers from least to greatest? Are the numbers in different forms? To make comparing easier, convert all the numbers to decimals. Then, plot those decimals on a number line and compare them! This tutorial shows you how!

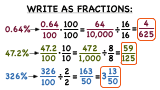
How Do You Turn a Percent Into a Fraction?

Looking for some practice converting percents to fractions? Then this tutorial was made for you! Follow along as this tutorial shows you how to convert a percent to a fraction. Then, reduce the fraction to put it in simplest form. Check it out!

How Do You Turn a Fraction Into a Percent?

Looking for some practice converting fractions to percents? Then this tutorial was made for you! Follow along as this tutorial shows you how to convert a fraction to a percent.Take a look!

How Do You Turn a Decimal into a Percent?

Converting decimals into percents is easier than you may think! To convert a decimal to a percent, just move the decimal point to places to the right and put a percent sign at the end! To see it done, check out this tutorial!

How Do You Use a Proportion to Find a Whole?

Taking a percent of a number? Trying to figure out the result? Use a percent proportion to solve! This tutorial will show you how!

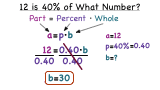
How Do You Use an Equation to Find a Whole?

Taking a percent of a number? Trying to figure out the result? Use a percent equation to solve! This tutorial will show you how!

How Do You Use Compatible Numbers to Estimate a Part of a Whole?

If you're trying to find the percent of a number, it may be helpful to use compatible numbers to find an estimated answer. Follow along with this tutorial to see how to use compatible numbers to estimate the percent of a number!

• Terms of Use

Common Core State Standards Initiative

Ratios & Proportional Relationships

Understand ratio concepts and use ratio reasoning to solve problems., analyze proportional relationships and use them to solve real-world and mathematical problems..

• Standards for Mathematical Practice
• How to read the grade level standards
• Introduction
• Counting & Cardinality
• Operations & Algebraic Thinking
• Number & Operations in Base Ten
• Measurement & Data
• Number & Operations—Fractions¹
• Number & Operations in Base Ten¹
• Number & Operations—Fractions
• Ratios & Proportional Relationships
• The Number System
• Expressions & Equations
• Statistics & Probability
• The Real Number System
• Quantities*
• The Complex Number System
• Vector & Matrix Quantities
• Seeing Structure in Expressions
• Arithmetic with Polynomials & Rational Expressions
• Creating Equations*
• Reasoning with Equations & Inequalities
• Interpreting Functions
• Building Functions
• Linear, Quadratic, & Exponential Models*
• Trigonometric Functions
• High School: Modeling
• Similarity, Right Triangles, & Trigonometry
• Expressing Geometric Properties with Equations
• Geometric Measurement & Dimension
• Modeling with Geometry
• Interpreting Categorical & Quantitative Data
• Making Inferences & Justifying Conclusions
• Conditional Probability & the Rules of Probability
• Using Probability to Make Decisions
• Courses & Transitions
• Mathematics Glossary
• Mathematics Appendix A

Curriculum  /  Math  /  6th Grade  /  Unit 1: Understanding and Representing Ratios  /  Lesson 9

Understanding and Representing Ratios

Lesson 9 of 18

Criteria for Success

Tips for teachers, anchor problems, problem set, target task, additional practice.

Use ratio reasoning to solve a three-act task.

Common Core Standards

Core standards.

The core standards covered in this lesson

Ratios and Proportional Relationships

6.RP.A.3 — Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.

The essential concepts students need to demonstrate or understand to achieve the lesson objective

• Make observations and pose questions to an incomplete problem.
• Make an educational guess and pose a possible solution pathway.
• Make adjustments to a ratio in order to create equivalent ratios.

Suggestions for teachers to help them teach this lesson

• Students have worked with three-act tasks in previous grades of the Fishtank math curriculum; however, as the first one in sixth grade, you may want to establish a culture or process in your classroom around how these are used.
• Students engage in MP.1 in this three-act task as they analyze the information given to them and determine how they can use equivalent ratios to fix the mixup. They must map out their own strategy and check their answers, making adjustments as needed.
• Students also discover how they can apply ratio reasoning to support them in understanding the math in the problem and determine a solution (MP.4).

Unlock features to optimize your prep time, plan engaging lessons, and monitor student progress.

Problems designed to teach key points of the lesson and guiding questions to help draw out student understanding

Act 1: Watch the prologue video to the " Nana's Paint Mixup " three-act task.

What do you notice? What do you wonder?

Guiding Questions

Nana's Paint Mixup by Dan Meyer is made available on  101Questions  under the CC BY 3.0 license . Accessed July 18, 2017, 4:33 p.m..

Act 2: How can we use equivalent ratios to fix this mix-up? 

Act 3: Watch the video answer . 

Was your answer reasonable? Why or why not?

Sequel: How many other ways to fix the mix-up can you find?

A set of suggested resources or problem types that teachers can turn into a problem set

Give your students more opportunities to practice the skills in this lesson with a downloadable problem set aligned to the daily objective.

A task that represents the peak thinking of the lesson - mastery will indicate whether or not objective was achieved

You’re mixing ingredients for cookies. The recipe says to combine 6 tablespoons, or ¾ stick, of butter with 1 cup of sugar. You accidentally mix in a whole stick of butter (8 tablespoons) with the cup of sugar. How can you fix this?

Student Response

An example response to the Target Task at the level of detail expected of the students.

The following resources include problems and activities aligned to the objective of the lesson that can be used for additional practice or to create your own problem set.

• Opportunity to review concepts and skills from previous lessons
• Dan Meyer's Three-Act Math Nana's Chocolate Milk

Topic A: Understanding & Describing Ratios

Define ratio and use ratio language to describe associations between two or more quantities.

Represent ratios using discrete drawings. Understand that the order of numbers in a ratio matters.

Create a free account to access thousands of lesson plans.

Already have an account? Sign In

Topic B: Equivalent Ratios

Define and find equivalent ratios.

Reason with equivalent ratios and determine if two ratios are equivalent.

Represent ratios using double number lines and identify equivalent ratios. 

Solve ratio problems using strategies including double number lines.

Find equivalent ratios using ratios with “per 1” unit.

6.RP.A.3 6.RP.A.3.B

Compare situations using equivalent ratios and double number lines.

Topic C: Representing Ratios in Tables

Represent ratios in tables.

6.RP.A.3 6.RP.A.3.A

Understand the structure of tables of equivalent ratios. Solve ratio problems using tables.

Solve ratio problems using tables, including those involving total amounts.

Compare ratios using tables.

Solve ratio problems using different strategies.

6.RP.A.1 6.RP.A.3 6.RP.A.3.A

Topic D: Solving Part:Part:Whole Ratio Problems

Solve part:part ratio problems using tape diagrams.

6.RP.A.1 6.RP.A.3

Solve part:whole ratio problems using tape diagrams.

Solve more complex ratio problems using tape diagrams.

Solve ratio problems using a variety of strategies, including reasoning about diagrams, double number lines, tables, and tape diagrams. Summarize strategies for solving ratio problems.

Request a Demo

See all of the features of Fishtank in action and begin the conversation about adoption.

Learn more about Fishtank Learning School Adoption.

Contact Information

School information, what courses are you interested in, are you interested in onboarding professional learning for your teachers and instructional leaders, any other information you would like to provide about your school.

Effective Instruction Made Easy

Access rigorous, relevant, and adaptable math lesson plans for free

• Get Started

Learning Lab Collections

• Collections
• Assignments

CCSS.Math.Content.6.RP.A Understand ratio concepts and use ratio reasoning to solve problems.

• CCSS.Math.Content.6.RP.A.1 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
• CCSS.Math.Content.6.RP.A.2 Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship.
• CCSS.Math.Content.6.RP.A.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
• Ratios and Images of African Art: Grade 6

My Learning Lab:

Forgot my password.

Please provide your account's email address and we will e-mail you instructions to reset your password. For assistance changing the password for a child account, please contact us

You are about to leave Smithsonian Learning Lab.

Your browser is not compatible with site. do you still want to continue.

Real World, Real Numbers: Ratio and Proportions

Mathematics

Level 6 Level 7 Level 8

What is this sequence about?

Proportional reasoning is important as it forms the basis of student learning in other mathematical domains such as measurement and geometry and financial mathematics (Siemon et al., 2018). It is a skill we often rely on daily when comparing the relationship of proportions.

This learning sequence aims to develop student understanding of the relationships between ratio and proportion in a range of everyday situations. Students will extend their understanding of fraction equivalence, fraction quantities and percentages to make sense of the multiplicative relationships that underpin proportional reasoning. By investigating proportional situations in real world contexts, students will have opportunities to simplify and compare ratios, divide quantities into ratios, and explore simple rates with a focus on the proficiency strands of problem solving and reasoning.

The sequence has been written by teachers for teachers. It has been designed to provide students with rich, engaging learning experiences that address the Victorian Curriculum. The sequence consists of four flexible stages, including suggested learning intentions.

There is a strong focus within this sequence on supporting students to develop the four mathematical proficiencies set out in the curriculum: Understanding, Fluency, Problem Solving and Reasoning, as well as their capacity for critical and creative thinking.

Overview of stages

1. Building Understanding of Ratios

Suggested Learning Intentions

• To recognise the relationships between quantities or measures in ratios

3. Comparing Ratios

• To apply our knowledge of equivalence to compare ratios

2. Finding the Unknown in Ratios

• To build fluency in applying our understanding of ratios to solve problems

4. Finding the Better Deal

• To evaluate different rates and prove that one is better than the other

Prior knowledge

Before you commence this sequence, it is suggested that you ensure your students are familiar with calculating equivalent fractions, simplifying fractions and comparing fractions. Students should also have some familiarity with making connections between fractions, decimals and percentages.

You can find support for building students’ understanding of these concepts in the following sections of the Mathematics Curriculum Companion :

Teaching strategies

The Mathematics Curriculum Companion provides teachers with content knowledge, suggested teaching and learning ideas as well as links to other resources. Resources are organised by Mathematics strands and sub-strands and incorporate the proficiencies: Understanding, Fluency, Problem Solving and Reasoning. The Companion is an additional resource that you could refer to when you are planning how you might use the sequence in your school.

The sequence highlights opportunities to apply the  High Impact Teaching Strategies (HITS) , which are a component of the Victorian Teaching and Learning Model . 

Students should be able to understand and use the following concepts and terms by the end of the learning sequence:

You can find definitions of some of these terms in the Glossary for the Mathematics Curriculum .

It is recommended that the explicit teaching of vocabulary occur throughout this learning sequence. The Literacy in Mathematics section of the Literacy Teaching Toolkit provides several teaching strategies with worked examples demonstrating how teachers can use literacy to support student understanding of mathematical language. A further set of strategies demonstrate how teachers can develop students' literacy skills to support their mathematical problem solving.

Opportunities for formative and summative assessment are identified at different stages of the learning sequence. Look for the 'Assessment Opportunity' icon.

You may want to develop a rubric to assess students’ progress. A range of Formative Assessment resources are available from the Victorian Curriculum and Assessment Authority. This includes a Guide to Formative Assessment Rubrics , a series of modules to support you to develop your own formative assessment rubrics, and sample rubrics across six curriculum areas that demonstrate how you can put formative assessment rubrics into practice in the classroom.

In developing a rubric, you may wish to co-construct assessment criteria with your students. Each stage of the sequence provides sample success criteria for students working at Level 7.

The Victorian Curriculum and Assessment Authority has published annotated work samples that provide teachers with examples of student learning achievement at multiple levels for each strand of the Mathematics curriculum.

Victorian Curriculum connections

This sequence addresses content from the Victorian Curriculum in Mathematics and Geography. It is primarily designed for Level 7, but also addresses the following content descriptions from Level 6:

The sequence can be used to assess student achievement in relation to the following Achievement Standards from the Victorian Curriculum: Mathematics Level 6:

• Students locate fractions and integers on a number line and connect fractions, decimals and percentages as different representations of the same number
• Students calculate simple fractions of a quantity.

This sequence addresses content from the Victorian Curriculum in Mathematics and Critical and Creative Thinking. It is primarily designed for Level 7, and addresses the following content descriptions:

The sequence can be used to assess student achievement in relation to the following Achievement Standards from the Victorian Curriculum: Mathematics Level 7:

• Students solve problems involving all four operations with fractions, decimals, percentages and their equivalences
• Students express fractions in their simplest form.

This sequence addresses content from the Victorian Curriculum in Mathematics and Geography. It is primarily designed for Level 7, but also addresses the following content descriptions from Level 8:

The sequence can be used to assess student achievement in relation to the following Achievement Standards from the Victorian Curriculum: Mathematics Level 8:

• Students estimate answers and solve everyday problems involving rates, ratios and percentages, with and without the use of digital technology.

Learning Progressions

The Numeracy Learning Progressions support teachers to develop a comprehensive view of how numeracy develops over time. You can use the Numeracy Learning Progressions to:

• identify the numeracy capability of your students
• plan targeted teaching strategies, especially for students achieving above or below the age-equivalent expected level in the Victorian Curriculum: Mathematics
• provide targeted feedback to students about their learning within and across the progressions.

The sequence is related to the following progressions:

Click on the Learning Progression to access more detailed descriptions of student learning at each level.

• Benefits to Participating Communities
• Participating School Districts
• Evaluations and Results
• Recognition Accorded
• National Advisory Committee
• Establishing New Institutes
• Topical Index of Curriculum Units
• View Topical Index of Curriculum Units
• Search Curricular Resources
• View Volumes of Curriculum Units from National Seminars
• Find Curriculum Units Written in Seminars Led by Yale Faculty
• Find Curriculum Units Written by Teachers in National Seminars
• Browse Curriculum Units Developed in Teachers Institutes
• On Common Ground
• Reports and Evaluations
• Articles and Essays
• Documentation
• Video Programs

Have a suggestion to improve this page?

To leave a general comment about our Web site, please click here

Share this page with your network.

Developing Proportional Reasoning

“How could they think their answer is even close to being correct? What were they thinking? Did they seriously just add those two numbers together? I didn’t teach it that way! Do they even know what a ratio is? Why are they cross-multiplying everything? Did they read the problem? Why are they not take the time to set up the proportion correctly?” Thoughts and questions like these ran through my mind when analyzing student work from my ratio and proportion unit last year. I have found that it is easy as a teacher to fall into this frustrating line of thinking, questioning whether or not I taught a certain skill correctly, if students are ever paying attention, or if some are even capable of applying sound proportional reasoning. Upon reflection, I concluded that the way I perceived my student’s deficits was at the very least flawed, and counterproductive to my practice. In writing this unit I aim to teach ratios and proportions in a way that promotes the development of proportional reasoning and avoids the dependence on rules and procedures that lead to shallow understandings. In order to drive my unit in a productive manner, I kept the following guiding questions at the forefront. What has obstructed the development of my students’ proportional reasoning? Why have students consistently made the same mistakes, employing similarly flawed reasoning in problem solving, and how are curriculum and instructional strategies contributing to these problems?

I teach at an elementary school on the southwest side of Chicago. We are a neighborhood school that is 95% low income and serves roughly 1,200 students in pre-kindergarten through eighth grade. This next year I will be teaching four sections of sixth grade math in a general education setting. According to district and school assessments, this upcoming class, by a significant margin, presents the most remedial needs in mathematics when compared to other grades at my school. They will be entering middle school with large deficits in the fundamental areas of fractions, operations and algebraic thinking. I chose to write my unit on the subject of ratios, proportions and proportional reasoning because the concepts overlap in almost all other areas in the middle grades math standards and is determined by the Common Core to be a major work the sixth grade (CCSS Initiative 2015). Developing a robust and conceptual understanding of ratios and proportions will be important in the effort of setting a solid foundation for the entire school year. Ideally, through this unit, students will become accustomed to learning conceptually before procedurally, setting the standard for attaining a deeper understanding of subsequent concepts and rational problem solving that utilizes sound reasoning. Besides its foundational nature, the subject of ratios and proportions offer venues to remediate gaps in my students’ prerequisite skills such as fractions, operations and measurement. Throughout the unit’s lessons, I will draw out these basic skills to demonstrate how these concepts extend to more advanced ratio and proportion problems.

Content Background

What proportional reasoning is not.

Consider the following problem: A recipe calls for 3 lemon wedges to make 12 ounces of lemonade. How many lemon wedges would you need to make 20 ounces of the same lemonade? To analyze deficits in my students’ proportional reasoning, I will offer three example responses to the lemon problem that represent some of the most common trends in the way past students ultimately approached ratio and proportion problems by the end of the unit.

Example A shows the use of the most widely utilized algorithm to find a missing value in a proportion often called cross multiply and divide, also known as “rule of three”. To utilize this algorithm, students need to find one value when given three. The student here arrived at the correct answer, but we can’t definitively tell if the student utilized proportional reasoning. The only thing we can be certain of is their ability to substitute numbers into an algorithm.

Example B shows the same algorithm being utilized. Here they set up the proportion incorrectly, leading them to an incorrect comparison. This response gives cause for worry, because there is no evidence of attending to and coordinating the different units to make an accurate comparison. A multiple choice test question would likely include this answer as a trap choice due to the common nature of this mistake. The unreasonableness of this answer is also evidence of the student’s narrow and procedural understanding.

Example C shows no evidence of proportional reasoning. Here addition is used to find the missing value; the rationale being that the ounces went up by eight, so the lemons must go up by the same amount. Instead of proportional reasoning, the student utilized additive reasoning by only considering the difference in magnitude of the two quantities. Until 6 th grade this type of thinking is of greater focus. (The CCSS Writing Team 2011) To employ proportional reasoning, students need to compare multiplicatively.

What Proportional Reasoning Is and Why it Matters

In my research I came across a wide range of definitions, attempting to explain the complexity of proportional reasoning. The term encompasses a wide range of concepts including ratio, multiplicative comparison, co-variation, proportion, rate, unit rate, and constant rate of proportionality. Having a solid grasp of these concepts is indeed required in proportional reasoning. However to include all of these elements in its definition, clouds the essence of what proportional reasoning is. To simplify and to cut to the core of this term, I will use the following definition:

Proportional reasoning is reasoning about proportional relationships.

Being able to understand the presence or absence of proportionality in the relationship between two quantities is of significant importance. It is a critical form of thinking that requires the firm grasp of elementary fraction, operation and measurement concepts and lays the groundwork for algebra and other higher levels of mathematics. (Lesh et al. 1988) For most of my students, proportional reasoning will be a new way of thinking within mathematics. Because of this, my unit aims to develop proportional reasoning by centering my instruction on understanding proportional relationships. The National Council of Teachers of Mathematics lays out ten different essential understandings of ratios and proportions for grades sixth through eight. I have developed the essential understandings for my unit from four of these. They are as follows:

Essential Understanding 1. Reasoning with ratios involves attending to and coordinating two or more quantities.

Essential Understanding 2. A ratio is a multiplicative comparison of two quantities, or it is a joining of two quantities in a composed unit.

Essential Understanding 6. A proportional relationship is an equality between two ratios. In a proportional relationship, the ratio of two quantities remains constant as the corresponding values of the quantities change. This is the constant rate of proportionality.

Essential Understanding 7. Proportional reasoning is complex and involves understanding that-

• If one quantity in a ratio is multiplied or divided by a particular factor, then the other quantity must be multiplied or divided by the same factor to maintain the proportional relationship

(Lobato et al. 2010)

When students can apply the above understandings flexibly to solve ratio and proportion problems, they will be exhibiting thorough proportional reasoning. To achieve this ambitious goal I will reflect on my past teaching of the subject and use research and my work with this seminar to develop better strategies and approaches.

Theory Behind Order, Problem Types, and Problem Contexts

“Implicit learning must reflect the desired explicit teaching.” This idea has been central in Roger Howe’s seminar “Problem Solving and the Common Core”. The concept stems from the premise that a large portion of student learning happens due to the order in which content is presented and the variety of problem types and contexts or lack thereof students are exposed to. To expand on this idea I will explain how order, problem type and context can impede the development of proportional reasoning and then outline how my unit will take a different approach.

In reflecting on my own practice, this concept of implicit teaching and learning is something that I often lose site of when designing lessons and analyzing curriculum. A general illustration of students implicitly learning from a lack of context is in the teaching of a triangle. A common mistake primary educators make is when they teach the basic elements of a triangle only using examples that are equilateral with a horizontal base. If this is the only manner in which students first see triangles, they are likely to implicitly learn that triangles are shapes that are limited to three equal side lengths with a horizontal base. Even though this was not explicitly taught, the majority of students will likely take on this narrow view of triangles due to the lack of context. Analogous to this example, if ratios and proportions are not taught in proper order and without a variety of problem types and contexts, narrow and insufficient proportional reasoning will likely develop. This unit will provide a purposeful sequence of concepts and a diversity of problem types that promote the essential understandings of ratios and proportions.

The typical progression of concepts learned in a similar unit is as follows:

• Students learn different ways to write ratios.
• Students learn that proportions are two equivalent ratios and can be found by multiplying both quantities by the same value.
• Students learn how to find unit rates by dividing both quantities by the second quantity.
• Students then are taught the cross-multiplication algorithm to solve proportion problems with missing values. (Lobato et al. 2010)

This order roughly outlines the progression that my district-mandated curriculum uses. There are several flaws with this order. Students are first introduced to the concept of ratios by identifying basic relationships such as red marbles to blue marbles or boys to girls with the purpose of teaching what is and how to set up a ratio. See two examples of such problems:

Example D: There are 6 blue marbles and 4 red marbles. Write a ratio comparing red to blue marbles and blue to red marbles.

Example E: There are 15 boys and 8 girls in class. What is the ratio of boys to the total number of students in class?

In the above problems aim to address the concept of ratio in isolation, however there is no purposeful context. Meaning, there is no proportional relationship for which these ratios might be the constant rate of proportionality. These problems simply prompt students to order quantities in the form of a ratio without reasoning about the relationship between the quantities. This approach could potentially lead to misconceptions about the fundamental idea of ratio and makes the concept seem arbitrary and abstract.

Another and even more harmful impact of this typical sequence is how early the cross-multiply and divide method is presented. When students are given this algorithm too early in the development of concepts around proportional reasoning, it turns off the thinking switch when solving problems. I have experienced this in my own classroom when presenting this strategy to solve proportion problems. Shortly after the procedure is given, it is the only method used. Kids find the algorithm to be quick, comfortable, and fool-proof. Very little thinking happens thereafter. “Proportional reasoning involves much more than setting two ratios equal and solving for a missing term.” (Lesh et al. 1988) This procedure is efficient and one that students should learn to utilize eventually. However, it should be avoided until students develop a conceptual understanding of proportions.

The sequence of my unit will have two principal objectives: (1) unlike traditional progressions, the sequence will keep the idea of a proportional relationship at the fore by developing the concepts of ratio in conjunction with the concepts of proportion, not in isolation, and (2) the sequence will introduce skills and strategies that make the concepts of ratios and proportionality more accessible before teaching any procedural algorithms.

Context of Problems

When first developing proportional reasoning, students need to work with problems that help students visualize and grasp the desired outcomes. If students are given problems with scenarios in which they cannot easily model for themselves, they are more likely to look for procedural solutions and abandon the task of reasoning. They should be exposed to simple, familiar contexts and extend to more complex and/or unfamiliar ones as proportional reasoning develops. (Cramer and Post 1988)

Lessons in my unit will first consist of problems that are accessible and of high interest to my students. The contexts will be tangible so that students can use their own experiences to deepen their understanding of concepts. Examples of these contexts are “chocolateness” of chocolate chip cookies, strength of fruit juice, cost per item, length of time it takes to run around a track, and crowdedness of a room. These scenarios are easy to visualize and will provide an entry point for all students in whole-group discussion. In addition, they demand proportional reasoning and give purpose to comparing the relationship of different quantities.

Problem Types

The variety and order in which different problem types are presented to students plays a significant role in the development of proportional reasoning. Students need to be exposed to a range of problem types so that they develop reasoning that can be generalized to all situations involving ratios. As is true with all areas of math, if a student’s problem solving is limited to a subset of problem types and if the key issues are never presented or discussed, they will likely develop a narrow and less flexible understanding of the area’s concepts. The curriculum that I have used in the past has taught specific proportional reasoning strategies in isolation and dealt only with specific problem types. For example, problems that require students to find a missing value are traditionally used to teach the cross-multiply and divide algorithm. If students do not see a substantial variety of problems, they tend to stop analyzing and reasoning through problems. Seeing the same problem type repeatedly elicits the same strategy repeatedly, and this leads to a fixed and inflexible use of reasoning when presented with a problem type that could require a different strategy or approach. To avoid this, my unit will consist of mixed problem sets that contain a combination of many types of problems so that students have space to apply their different forms of reasoning under varying conditions.

There are three different problem types that require the use of proportional reasoning. They are: (1) missing value, (2) numerical comparison, and (3) qualitative prediction and comparison. (Post, 1988) The following sections provide a description and example of each type.

Missing Value

In the various curriculums I analyzed, missing value problems constituted a large majority. A problem of this type gives one complete ratio with two given quantities and another incomplete but proportional ratio with only one given value. Consider the following problem:

36 chocolate chips are used to make 6 chocolate chip cookies. If 12 cookies are made with same number of chips per cookie, how many chips are needed?

Here the complete ratio of 36 chips to 6 cookies is given with the task of finding the missing number of chips for 12 cookies in a proportional relationship. The degree of difficulty changes with different numerical contexts. The problem is generally easier if the relationship between the ratios or within the ratio is integral, as in the previously mentioned cookie problem. When the relationship between or within is fractional, the problems of course become more difficult. Because this unit aims to introduce and develop proportional reasoning for the first time, whole number relationships will be used to start with. Once students are comfortable with this idea of proportion, students will be exposed to proportional relationships with larger whole numbers, unit fractions, and general fractions with gradually increasing numerators and denominators. Using this strategy will allow different abilities to be challenged at an appropriate level throughout the unit.

Numerical Comparison

Numerical comparison problems require the evaluation of two given ratios. Consider the following problem:

Mixing flavored powder with water makes Kool Aid juice. Grandma made Kool Aid by mixing 3 cups of water with 9 tablespoons of powder. Grandpa made Kool Aid by mixing 6 cups of water with 12 tablespoons of powder. Which Kool Aid will taste stronger?

In order to reasonably answer the question, students must compare the two given ratios, 3 cups to 9 tablespoons and 6 cups to 12 tablespoons. This problem type requires students to apply proportional reasoning and determine a greater or lesser value in relation to the question. Although these problems do not explicitly ask the solver to express a proportional relationship, one must reason with the implicit ones to answer the question. Here, a proportional relationship was implied in each of the recipes. Grandma would use 3 tablespoons of powder for every cup of water and Grandpa soul use 2 tablespoons to every cups of water.

Qualitative Prediction

My analysis revealed that qualitative prediction is the most unrepresented problem type in middle school curriculum. It consists of a scenario that requires a comparison that is not dependent on numerical data. Consider the following problem:

Two friends each hammered a line of equally spaced nails into different boards  using the full length of each board. Bill hammered more nails than Greg. Bill’s board was shorter than Greg’s. On which board are the nails hammered closer? (Cramer and Post 1988)

The problem requires the comparison of the board length and number of nails. The absence of numbers forces the solver to focus on the relationship of two different ratios in order to answer the question. The implicit proportional relationship that must be considered is the length of a row of evenly spaced nails to the number of nails. This type of problem is valuable because it demands proportional reasoning and provides no opportunity to apply a procedure or algorithm. Although I have found that this type of problem is not typically assessed, it will be a valuable exercise in developing a complete understanding of proportion.

Unit Learning Outcomes

Attending to and coordinating two quantities- essential understanding #1.

Students will first develop the concept of ratio by solving a set of comparing and missing value problems. Ultimately students need to see ratios as describing the relationship between two quantities. “Before children are able to reason with ratios, they typically reason with a single quantity.” (Lobato et al. 2010) Students must first reach this understanding of attending to and coordinating two quantities before they can reason with ratios. Consider the following problem that will be used to develop this concept.

Let the two rectangles represent different sized cow pens and the ovals represent equally sized cows. Pen A has an area of 8 square yards. Pen B has as area of 4 square yards. Which cow pen is more crowded?

The point that will be drawn from this example is that the relationship between two different quantities, in this case number of cows and area, which can be expressed, for example, in number of square meters, needs to be reasoned with in order to answer the question. A first intuition might be to count the number of cows in order to determine crowdedness. In this line of thinking, a student is only attending to one quantity. This logic can be easily proven wrong by drawing a grid over the rectangles showing that pen A has 1 square yard for every cow whereas pen B only has 4 square yards for 5 cows making it more crowded. Another way to approach this problem is by doubling B making the area the same as pen A but the number of cows greater by 2. This too visually shows that pen B is more crowded than A. After students have grasped the concept of attending to different quantities and their relationship, they will be explicitly taught the different ways of notating ratios.

Although the focus of the cow pen problem is on prompting students to begin using ratios to coordinate and compare two different quantities, it also implicitly calls students to consider proportional relationships. For example students might arrive at the conclusion that pen A has 4 cows per 4 square meters, thus arriving at a proportional ratio. This link should be explicitly shown to students in discussing ratio problems. Even though the unit starts with a focus on ratio, ideas of a proportional relationship will be addressed in conjunction. When a solid foundation of ratio and its utility is established, students will move on to explicitly grapple with proportions.

Proportion - Essential Understandings #2 and #7

Two ratios that are in proportion are also called equivalent. This concept will be initially developed by applying it to familiar contexts such as measurement conversions and price per item. Consider the following problem:

John had 3 yardsticks and he noticed that there were 9 feet in 3 yards. He used the yardsticks to measure the length of the classroom. The classroom measured 12 yards long. What is the length of the classroom in feet?

This problem provides an excellent entry point to understand proportions in two different ways. One approach to this problem is to look across the ratios and see that 12 yards is 4 times as many as 3. So to complete this proportion one can multiply 9 feet by 4 to get 36 feet. In addition, students should ultimately see the relationship within both ratios realizing that 9 is 3 times 3 so 12 can be multiplied by 3 to reach the same answer of 36. This, I will later explain, is the constant rate of proportionality (namely 3 feet per yard), a more advanced concept. 

(9 ft × 4)/(3 yd × 4) = (36 ft)/(12 yd)

(9 ft)/(3 yd × 3) = (36 ft)/(12 yd ×3)

The first example demonstrates the understanding that two corresponding quantities in one ratio will relate to any two other corresponding quantities by the same factor. In this case the quantity 9 feet relates to the quantity 36 feet by a factor of 4, as does 3 yards to 12 yards. This is the fundamental property of proportional relationships, and should be focused on first. The second example demonstrates that there is a constant relationship within a ratio and that is the same for all other proportional ratios. In this case the constant is 3. So for any number of yards, the number of feet will be 3 times as many. In this example it is obvious, due to its being a simple whole number, but when the constant rate of proportionality is larger or fractional, this concept becomes more difficult for students to grasp. Both examples are important uses of multiplicative comparison and both will be developed and taught explicitly via these types of problems. With this knowledge students can evaluate ratios for proportionality and generate equivalent ratios. In order to develop flexible proportional reasoning students need these understanding before learning any algorithm.

Taught alongside multiplicative reasoning should be the idea of a unit rate. A unit rate is a version of a ratio that expresses the relationship between a quantity and 1 unit of the other quantity. Unit rates are only defined when the units of each quantity are specified. Often there is an obvious or convenient unit to choose for the denominator, but the fact that a choice has been made is important and should be addressed. Once the units of each quantity have been chosen, the unit rate is a well-defined number. Common examples of unit rates seen in an everyday context are miles per 1 hour or cost per 1 item. Consider the following problem:

If 12 sodas cost $18, how much would 20 sodas cost?

Using the unit rate approach, students can find the cost of 1 soda by dividing 18 by 12 to find the unit rate of $1.50 per 1 soda and then multiply this value by 20 to find the cost of 20 sodas. Ratios within a proportional relationship will always have the same unit rate. This is because the unit rate is the constant rate of proportionality, expressed in the given units. Similar to the multiplicative approach, finding the unit rate can help evaluate proportional relationships and find equivalent ratios. Research shows that students used the unit rate strategy more frequently due to its more procedural and intuitive nature. To make sure that students do not narrowly rely on this strategy it is important to show its relation to multiplicative comparison. (Cruz 2013)

Constant Rate of Proportionality- Essential Understanding 6

When comparing multiplicatively within a ratio and when finding the unit rate, the constant rate of proportionality is defined. However this concept will be taught last; it is not enough to simply understand that the unit rate is the constant rate of proportionality. It needs to be understood as a relationship. Consider the following statement letting the variable k represent the constant: if quantities a and b are in proportional relationship, then for any pair of corresponding values,

In any ratio  a/b = k so a = kb

The constant explicitly shows the relationship between the two quantities in the ratio, a:b. This relationship is that for every b there are k times as many a . To reach this understanding it is useful to ask students questions such as: How many times bigger/smaller is a compared to b ? For every increase to b what is happening to a ? Comprehending this idea is an important landmark in proportional reasoning. Ultimately students will be tasked with creating an equation such as the one above to express a proportional relationship. Because of its importance in their future work in grades seven and eight with linear equations and functions, a conceptual understanding of the meaning of a constant rate of proportionality is critical.

A Note on Algorithms

This is an introduction to ratios and proportional reasoning. Students will be developing this sense over the course of the next two years. Teaching of standard algorithms could impede the future development of proportional reasoning. Although my standard curriculum introduces the cross multiply and divide algorithm half way through the unit, I will hold off on teaching this strategy until I am confident in my students’ understanding of what a proportional relationship is.

Teaching Strategies

In the following sections I explain three important strategies that I will use to develop proportional reasoning. These approaches will be taught in the order they are explained in this section, but will not be used in isolation. I will explicitly prompt my students to use all strategies throughout the unit so that they are solving problems with a more robust toolkit.

Ratio Tables

Ratio Tables will be explicitly taught and referred to as a strategy in understanding and solving problems. This form of modeling helps represent relationships between two variables by placing the given data of a scenario into an organized table. See the following example.

Mr. Bingea ran 6 laps around the track in 12 minutes. Ms. Barret ran 12 laps around the track in 18 minutes. Compare their speeds.

The bolded numbers represent the given data from the problem. With this ratio table, proportional reasoning is seen if you follow the numbers from left to right. The quantities are multiplied by obvious factors, finding similar values for both relationships, making it easier to compare. Giving students this form allows them to see the proportional relationships in multiple iterations reinforcing the notion of a constant rate of proportionality. In addition to using this structure to solve and understand problems, students will also be presented tasks where they are given tables with complete or missing data sets and prompted to draw conclusions.

Double Number Line

A double number line is an important tool that provides a visual representation of a ratio and further demonstrates the constant rate of proportionality. See the following example:

Zack’s orange paint is made by mixing 3 cups of red for every 4 cups yellow paint. How many cups of red would be used if 10 cups of yellow were used?

This model vividly teaches the attention to and coordination of different quantities. Here the ratio of 3 to 4 is meaningfully represented in the relation between the length scales on the two lines. The answer to the problem is achieved by reasoning that 10 is half way between 8 and 12, therefore the solution lies half way between 6 and 9 which is 7.5. This example is advanced and should not be used to introduce the double number line. Instead examples where there is an integral unit rate should be used to first introduce ratios this way. It is also prerequisite that students have a firm grasp of representing value on a number line. Students must be comfortable with length measurement, and the need to specify a unit length on a given number line. If not, this skill should be reviewed before introducing the double number line.

Another way of visually reasoning with ratios and proportions is by means of a tape model. Consider the following example:

In the school cafeteria, 3 apples are eaten for every 7 oranges eaten. If 80 pieces of fruit have been eaten, how many of each fruit can we predict have been eaten?

In the tape model, 3 boxes represent 3 apples and 7 boxes represent 7 oranges. The given ratio is clearly seen with a total of 10 boxes for the 10 pieces of fruit. Because the ratio will not change in a proportional relationship we can ask ourselves: What does each box represent if there are 80 pieces of fruit? Because there are 10 boxes of equal value, it is apparent that each box represents 8 pieces of fruit. So we can predict that there would have been 24 apples and 56 oranges eaten. The visual nature and focus on the constant rate of proportion makes this model a valuable tool in this unit. However the order of introducing this model must be considered. This strategy will be introduced after the previous strategies and when students have a sufficient understanding of the multiplicative relationship of ratios in a proportional relationship. They are excellent models to represent and solve missing value problems but have the potential to be used by students without a conceptual understanding. If this is the case, students tend to use this strategy as an algorithm without understanding the reasoning behind the model.

Structured Problem Solving

The general form of lessons I will use in this unit will be centered on structured problem solving. This is different when compared to a typical gradual release lesson format where students are taught a strategy explicitly, practice the strategy with heavy teacher guidance, and then eventually apply it through independent practice. In a problem-based format, students are presented a problem to be first worked on independently. Here students will apply their own mathematical knowledge in an effort to develop strategies to reach a solution. Once students have had time to work independently, their different strategies and solutions are shared and discussed in groups or as a class. During this time students will be able to see multiple approaches, discuss misconceptions, and come to new conclusions about the material. The discussion must be carefully facilitated in order to reach the desired outcomes for the lesson. If all student ideas have been exhausted and the strategies or understandings the lesson set out to achieve have still not been reached, explicit teaching will then take place. Finally the students are given a set of additional problems to apply and practice what they learned from the problem solving and the discussion. The key idea behind a structured problem solving approach is that students are first given the opportunity to reason and construct their own concepts and strategies, which leads to a deeper understanding of the content covered in a given lesson. In the pursuit of nurturing proportional reasoning, a new way of thinking for 6 th graders, this approach will be fundamental.

Structured problem solving is laid out in Akihiko Takahashi’s paper titled, “Characteristics of Japanese Mathematics Lessons”. Takahashi stresses that in addition to the attention devoted to extensive discussion, the selection of problems and activities needs to be carefully considered as well. (Takahashi 2006) For the purpose of developing proportional reasoning, the progression of problems in this unit is designed to bring out concepts and strategies that cohesively build on each other. In general, each lesson will present a new problem scenario for students to solve. This scenario will be engaging and include the use of visuals, multi-media, and props to ensure all students access and become invested in the problem. After the structured problem-solving process has taken place, students will be given a similar scenario if not the same but with different numbers. These exercises will give students the opportunity to process, apply, and generalize the previously discussed strategies and understandings.

The problems that I will use to center my lessons around require a greater explanation and use of images. For access to these, visit the website www.mrbingea.blogspot.com or email me at [email protected].

Number Talks

A number talk is a five to ten minute routine that I will use to start most class periods. The purpose of this activity is to review prerequisite or fundamental concepts to the day’s lesson in an efficient and meaningful way. As stated earlier, proportional reasoning requires the mastery of many skills learned prior to sixth grade, and it is likely that my students will have large gaps in these areas that could hinder their learning about proportional relationships. I will use number talks to gradually remediate and develop these more basic understandings throughout the entire year. The routine follows a simple format that is centered on the purpose of bringing all students into the thinking and discussion around the lesson’s concepts.

A number talk begins by all students putting away materials to ready themselves for the prompt that will only require the use of mental math. The problem is presented on the board for all students. They then solve the problem mentally and put their thumbs up when they have reached a solution. Next, volunteers share their strategies as the teacher models each student’s line of thinking on the board. Finally the class discusses the accuracy and reasoning of each strategy. By the end of this discussion students can see multiple, valid approaches to solving a relatively simple problem. Mastery of any one strategy is never the goal for a single number talk; instead it is a daily practice for students to gradually acquire a wide range of skills with basic operations and number sense. For a more thorough description of number talks refer to the book written by Cathy Humphreys and Ruth Parker, “Making Number Talks Matter”. It details the procedure as well as how the teacher should facilitate student thinking and discussion. The book also gives example prompts and different strategies to help students develop. (Humphreys and Parker 2015)

The concept of focus in each number talk will be directly related to the lesson’s learning objectives. For example, when teaching the concept of equivalent ratios in a proportional relationship, the number talk will cover the concept of equivalent fractions. This sets up the opportunity to make connections to these foundational concepts in later class discussions. The following table shows several problems that will be used in number talks to prime lessons in this unit and the linked foundational concepts.

Each of these problems requires a skill or concept covered in grades three through five. Students will most likely know or be partially familiar one way to solve each problem. Through this routine students will be tasked with generating multiple strategies to solving these problems, making students more flexible with numbers and operations and ultimately being able to better access concepts within proportional reasoning.

Appendix 1- Standards

This unit has been written in accordance to the Common Core State Standards, which have been adopted by Chicago Public Schools. Specifically this unit will cover a set of standards within the strand of ratios and proportional relationships.

6.RP.A.1 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. 

6.RP.A.2 Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship. 

6.RP.A.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams or equations.

6.RP.A.3.a Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.

6.RP.A.3.b Solve unit rate problems including those involving unit pricing and constant speed.

6.RP.A.3.d Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities

Appendix 2- Sample Problems

Below is a set of sample 6 th grade problems for ratios and proportions. These are problems that will be used for practice and assessment throughout the unit. They are not problems that will be used for the basis of structured problem solving-based lessons.

The ratio of the number of boys to the number of girls at a school is 4:5. If there are 120 boys, how many students are there all together?

Sam’s two new aquariums each hold exactly 200 gallons of water. One aquarium will hold small fish and the other will hold large fish. He will buy 5 small fish for every 10 gallons of water in the aquarium. He will buy 8 large fish for every 40 gallons of water in the aquarium. What is the total number of fish Sam will have? What will be the ratio of Sam’s small fish to large fish?

A total of 300 trees will be planted in a park. There will be 2 pine trees planted for every 3 maple trees planted. How many of each type of tree will be planted in the park?

A food company that produces peanut butter decides to try out a new version of its peanut butter that is extra crunchy, using twice the number of peanut chunks as normal. The company hosts a sampling of its new product at grocery stores and finds that 5 out of every 9 customers prefer the new extra crunchy version. If the company is planning to produce 90,000 containers of crunchy peanut butter, how many of these containers should be the new extra crunchy variety, and how many of these containers should be the regular crunchy peanut butter?

The producer of the news station posted an article about the high school’s football championship ceremony on a new website. The website had 500 views after four hours. Create a table to show how many views the website would have had after the first, second, and third hours after posting, if the website receives views at the same rate. How many views would the website receive after 5 hours? (It should be noted here that “same rate” means: in any two equal time periods, there are the same number of views.)

Hank bought 5 meters of ribbon for $10. How much does the ribbon cost per centimeter?

A runner ran 20 miles in 150 minutes. If she runs at that speed, how long would it take her to run 6 miles? How far could she run in 15 minutes? How fast is she running in miles per hour? What is her pace in minutes per mile?

Sally drives 66 miles in 3 hours and Molly drives 72 miles in 4 hours. What is the difference between their average speeds, in miles per hour?

A stand is selling 8 mangos for $10 at a farmers’ market. The grocery store is selling 12 mangos for $15. Which has a cheaper deal on mangos, the farmers’ market or the grocery store?

A line measures 30 centimeters long. A second line measures 500 millimeters long. Which line is longer?

Who walks at a faster rate: someone who walks 60 feet in 10 seconds or someone who walks 42 feet in 6 seconds?

During the winter of 2012–2013, Buffalo, New York received 22 inches of snow in 12 hours. Oswego, New York received 31 inches of snow over a 15-hour period. Which city had a heavier snowfall rate?

One math student, John, can solve 6 math problems in 20 minutes while another student, Juaquine, can solve the same 6 math problems at a rate of 1 problem per 4 minutes. Who works faster?

Bibliography

“6-7 Ratios and Proportional Relationships.”. 2-15 Progressions for the Common Core State Standards in Mathematics. The Common Core Standards Writing Team, 26 Dec. 2011. Web. 30 July 2015.

“Grade 6 Ratios & Proportional Relationships.” Grade 6 Ratios & Proportional Relationships. Common Core State Standards Initiative. 2015. Web. 30 July 2015.

"Grade 6 Mathematics." Engage NY Grade 6 Mathematics. NYSED, 2015. Web. 29 June 2015

"My Achievement Network." ANET Standards. Achievement Network, 2015. Web. 29 June 2015.

"Progression for the Common Core State Standards in Mathematics" (2011): Institute for Mathematics and Education. University of Arizona, 26 Dec. 2011. Web. 29 June 2015.

de la Cruz, Jessica A. Selecting proportional reasoning tasks [online]. Australian Mathematics Teacher, The, Vol. 69, No. 2, 2013: 14-18. Web. 31 Jul 15.

Humphreys, Cathy, and Ruth E. Parker. Making Number Talks Matter: Developing Mathematical Practices and Deepening Understanding, Grades 4-10. Stenhouse Publishers, 2015. Print.

Lamon, Susan J. Teaching Fractions and Ratios for Understanding: Essential Content Knowledge and Instructional Strategies for Teachers. Mahwah, NJ: Erlbaum, 1999. Print.

Lesh, R., Post, T., & Behr, M. Proportional Reasoning. Number Concepts and Operations in the Middle Grades (pp. 93-118). Reston, VA: Lawrence Erlbaum & National Council of Teachers of Mathematics. 1988. Print.

Lobato, Joanne, Amy B. Ellis, and Randall I. Charles. Developing Essential Understanding of Ratios, Proportions, and Proportional Reasoning for Teaching Mathematics in Grades 6-8. Reston, VA: National Council of Teachers of Mathematics, 2010. Print.

Takahashi, Akihiko. “Charactersitics of Japanese Mathematics Lessons.” APEC International Conference on Innovative Teaching Mathematics through Lesson Study, 2006. Print.

Comments (0)

Be the first person to comment

SATs Tutoring Programme

"Seeing our 2023 maths results has highlighted what I already knew about the impact - it's brilliant!"

Hundreds of FREE maths SATs resources!

SATs practice papers, SATs revision packs, SATs intervention lessons and more!

20 Year 6 Ratio Questions And Answers: From Easy To Hard

Emma Johnson

Year 6 ratio questions are an important aspect of KS2 maths and pupils must have secure place value, division facts and times tables knowledge to understand ratio.

Here we provide a collection of 20 problem solving ratio and proportion questions that cover the concepts pupils may encounter and can be used as practice questions ahead of the Key Stage 2 SATs.  

This article also looks at the key terminology children need to confidently answer Year 6 ratio questions.  

• How often do ratio questions appear in the KS2 SATs?

Ratio questions appear less frequently in the SATs exams than some of the other national curriculum objectives. However, it is important that children can approach these questions confidently to help prepare them for wider life and deepen their knowledge of ratio in secondary school. 

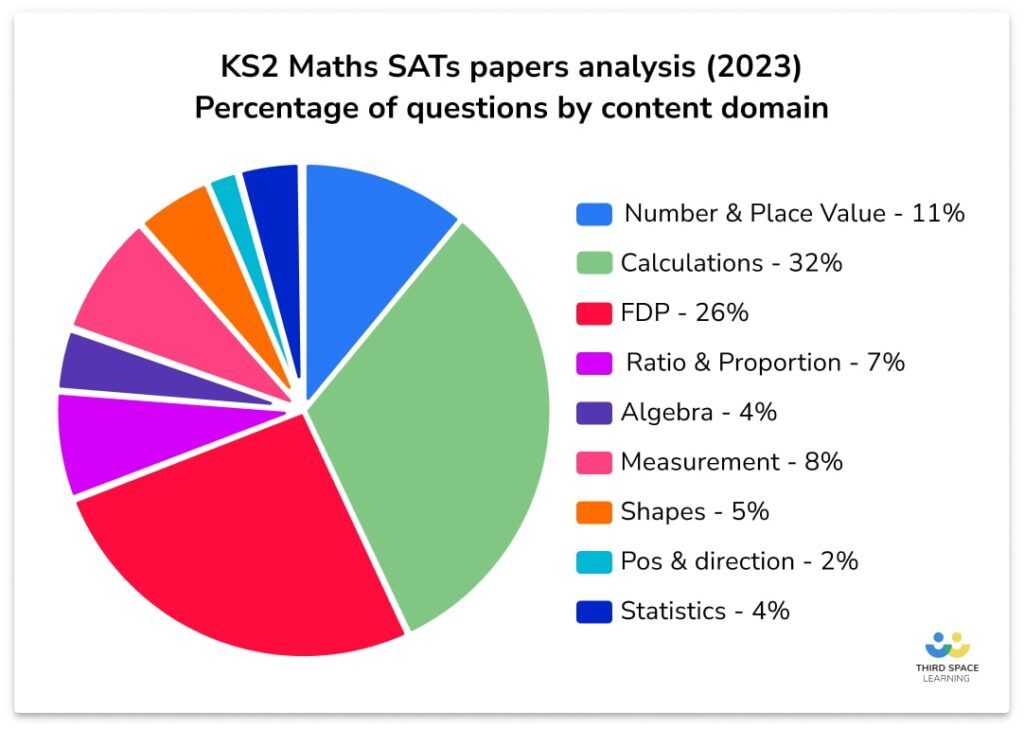
When looking at the SATs questions by topic , in the 2023 papers, ratio and proportion accounted for 7% of all questions across the three maths papers. 

Year 6 ratio questions: problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts

Year 6  ratio questions: problems involving the calculation of percentages and percentages for comparison, year 6 ratio questions: problems involving similar shapes where the scale factor is known or can be found, year 6 ratio questions: solve problems involving unequal sharing and grouping using knowledge of fractions and multiples, year 6 ratio questions key terminology.

To obtain a secure knowledge of ratio and answer these maths questions in Year 6 securely, children must have a strong understanding of the terminology associated with ratio and proportion. 

Key terms Year 6 pupils will need to have an understanding of include:

• Ratio : Explains how much of one thing there is in relation to another thing.  For example, the ratio of boys to girls is 2:3. This means there are 2 boys for every 3 girls.
• Proportion: This explains what the fraction is compared to the whole.  For example, there are 20 pieces of fruit (the whole) and 1 in 4 of those pieces of fruit are bananas (the proportion).
• Equivalent ratios: Ratios can have the same relationship but be written differently.  For example, 1:2 and 2:4 are equivalent ratios. 
• Factors: Ths is a number which divides into a number exactly. For example, 4 is a factor of 12 and 4 divides into 12 exactly 3 times. 
• Highest common factor: The highest number that can be divided exactly into 2 or more numbers. For example, the highest common factor of 12 and 18 is 6. It is the highest number that can be divided into 12 and 18.  
• Simplest form: This is the simplest way of showing the ratio. Both both parts of the ratio must be divided by the highest common factor.  For example, 12:18 in its simplest form is 2:3 when both parts are divided by the highest common factor of 12 and 18, which is 6. 
• Relative size: How large something is compared to another object.
• Missing value: The quantity or part of the ratio that isn’t initially known or provided. If you only have one part of the ratio, the other part is the missing value.
• Percentage: A ratio expressed out of 100, making it easy to compare things.  For example 75% means 75 out of 100.
• Comparing ratios: Establishing whether one ratio is less than, greater than or equal to another ratio. For example 1:2 = 2:4 but 1:2 > 1:3
• Comparison of ratio: Comparing the relationship between two or more ratios.
• Scale factor : For 2 similar shapes, the ratio of the corresponding lengths.
• Scaling ratios: Making a ratio bigger or smaller by multiplying or dividing each part by the same number.
• Unequal sharing: Using ratio to share things but not in an equal way. For example, John gets 2 red sweets for each of Daisy’s 3 green sweets.

200 arithmetic and reasoning questions for Year 6

Download 100 free arithmetic questions and 100 free reasoning questions for Year 6. Includes answers and mark scheme.

How will these Year 6 ratio word problems help pupils deepen their understanding?

KS2 maths assessments may present ratio questions in different formats:  

• Multiple choice
• Short answer questions
• Extended response questions

Exposure to a variety of ratio word problems will help pupils build familiarity with the different types of SATs questions and develop strategies for solving them. 

Practising ratio and proportion problems in real-life, relatable contexts helps ensure pupils understand and secure concepts.  

Frequent exposure to a range of ratio questions also helps develop pupils’ confidence when faced with them in their Key Stage 2 maths assessments.

This sequence of Year 6 ratio questions becomes progressively harder, enabling pupils to deepen their understanding. Questions may also challenge students who are working at greater depth. 

20 Year 6 ratio questions and answers

This first National Curriculum objective requires pupils to compare the 2 sizes or quantities. One value in the comparison may be missing or unknown.  

To complete the ratio, children must determine the missing value. 

Year 6  ratio question 1  

The ratio of red counters to yellow counters is 3:1. There are 12 counters altogether. How many are there of each colour?

Answer: 9 red counters and 3 yellow counters.

3:1 = 4 parts. 4 × 3 = 12

Year 6  ratio question 2

Chloe is making a necklace using purple and silver beads in a ratio of 2:1. If she uses 16 purple beads, how many silver beads will she use?

Answer: 8 silver beads

Year 6  ratio question 3  

Jared is making vegetable soup, using 200g of tomatoes, 120g of onions and 60g of mushrooms. If Jared uses 600g of mushrooms, what weight of onions will he need to use?

Answer: 360g of onions

200 × 3 = 600g

120 × 3 = 360g

Year 6  ratio question 4  

If the ratio of green sweets to red sweets in a bag is 2:3. How many of each colour are in a bag of 30 sweets?

Answer: 12 green sweets and 18 red sweets.

2:3 is a total of 5. For a total of 30, we need to work out 2:3 six times.

Year 6  ratio question 5  

Students in year 6 have chosen their favourite sport. They chose tennis and football in a ratio of 3:5. If there are 80 children in the year group, how many chose football?

Answer: 50 chose football

3:5 = 8 parts.

8 × 10 = 80

3 × 10 = 30

5 × 10 = 50

Calculating percentages involves expressing a part of a whole as a percentage. 

Children need to be confident applying the concept of percentages to different measures and quantities. 

Once pupils have mastered the basic percentage calculations, they can then compare quantities and values and apply their understanding of percentages to interpret pie charts.

Year 6  ratio question 6

Calculate 45% of 740

Answer: 333

40% = 74 × 4 = 296

 40% = 296 + 37 = 333

Year 6  ratio question 7  

Sam arrives at school at 9am each day and leaves at 3pm. What percentage of the day is he at school?

Answer: 25% of the day.

9 – 3 = 6 hours

\cfrac{6}{24} hours of the day = \cfrac{1}{4} of the day

\cfrac{1}{4} = 25%

Year 6  ratio question 8  

In a school, Year 6 has 24 boys and 36 girls. What percentage of the year group are boys?

Answer: 40% are boys

24 + 36 = 60

\cfrac{24}{60} = \cfrac{4}{10} = 40%

Year 6  ratio question 9

Mason wanted to buy a pair of jeans in the sale. The original price was £45 but they were reduced by 15%. How much did he pay?

Answer: £38.35

10% of £45 = £4.50

5% of £45 = £2.25

15% of 45 = 6.75

45 – 6.75 = £38.25

Year 6  ratio question 10  

A shop is selling hoodies. One has a full price of £18 but has a 20% discount, the other has a full price of £20 but has a 35% discount. Which hoodie is the cheapest in the sale?

Answer: The second hoodie is cheaper

10% of £18 = £1.80

20% of £18 = £3.60

20% discount = £18 – £3.60 = £14.40

10% of £20 = £2

30% of £20 = £6

5% of £20 = £1

35% of £30 = £7

35% discount = £20 – £7 = £13

Free resource: Year 6 Calculating Ratio Worksheet

Shapes may be considered similar if they have the same shape but not the same size. For example,  their corresponding angles are equal and their corresponding sides are proportional.

Here, the scale factor refers to a ratio that describes how much one shape has been scaled, either enlarged or reduced, in relation to another similar shape. 

Year 6 pupils need to be able to solve problems related to similar shapes when the scale factor is either known or can be determined if the scale factor can be found. 

Year 6  ratio question 11  

Oliver says that a scale factor of 4 means the new shape is four times bigger than the original shape. Is Oliver correct? Explain your answer

Answer: No. A scale factor of 4 means each side is multiplied by 4. For example, if a square with sides of 1cm was 4 times bigger, the area would go from 1cm² to 4cm². If each side was 4 times bigger, the square would have an area of 16cm²

Year 6  ratio question 12  

Draw a rectangle 4cm × 6cm

Now enlarge the rectangle by a scale factor of 3. What are the new measurements of the rectangle?

Answer: A rectangle drawn with a length of 18cm and width of 12cm

Both sides will be 3 x as long

4cm × 3 = 12cm

6cm × 3 = 18cm

Year 6  ratio question 13  

What would the dimensions of a rectangle with a length of 6.5cm and a width of 4.5cm be, if it was enlarged by a scale factor of 3?

Answer: length 19.5cm, width 13.5cm.

Year 6  ratio question 14  

Draw a right-angled triangle with a base of 7cm and a height of 3cm.

No enlarge the right-angled triangle by a scale factor of 3.5

Answer: A right-angle triangle with a base of 24.5cm and a height of 10.5cm.

Year 6  ratio question 15  

Draw a right-angled triangle with a base of 9cm and a height of 5cm.

Draw a new right-angled triangle using a scale factor of \cfrac{1}{2} . 

Answer: A triangle drawn with a base of 4.5cm and height of 2.5cm

More Questions: Year 6 Using Scale Factors Worksheet

Pupils must apply their understanding of fractions and multiples to solve problems involving sharing or grouping unequal quantities. 

This includes: 

• Distributing a quantity among a group of people or containers with different capacities
• Finding the total quantity when given fractional parts of a whole
• Exploring relationships between fractions and multiples when dealing with unequal sharing or grouping situations.

Year 6  ratio question 16

If 600g of tomatoes are needed in a tomato soup recipe for 6 people. How many grams of tomatoes would be needed if there were only 4 people?

Answer: 400g

600 ÷ 6 = 100g

100 × 4 = 400g

Year 6  ratio question 17  

A book has 144 pages in total and is split into 6 chapters. How many pages are there in \cfrac{2}{6} of the chapters?

Answer: \cfrac{2}{6} = 48 pages

144 ÷ 6 = 24

2 × 24 = 48

Year 6  ratio question 18  

Sam and Amy received £480 between them for Christmas. If Sam received £60 more than Amy, how much did they each receive?

Answer: Sam: £270 Amy: £210

£480 – £60 = £420

£420 ÷ 2 = £210

£210 + £60 = £270

Year 6  ratio question 19  

Rosie planted some seeds in the garden. For every 5 seeds she planted, only 3 grew into flowers. If 15 flowers grew, how many seeds did she plant?

Answer: 25 seeds planted 

Year 6  ratio question 20  

A cinema has sold \cfrac{3}{8} of the tickets for the 9pm film. So far they have sold 114 tickets. How many tickets will they have sold if they sell all of them?

Answer: 304 tickets

114 tickets = \cfrac{3}{8}

\cfrac{1}{8} = 114 ÷ 3 = 38

38 × 8 = 304

Free resources for ratio and proportion:

• Year 6 arithmetic questions
• Fraction Questions For Year 6
• Year 6 algebra questions
• Year 6 Introducing Ratio Worksheet 
• Year 6 Ratio Independent Recap Worksheet  
• 24 Ratio Word Problems for Year 6 to Year 8 With Tips On Supporting Pupils’ Progress
• Ratio Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included
• Ratio – GCSE Maths – Steps, Examples & Worksheet

Ratio is how much of one thing there is in relation to something else. For example, for every 2 girls in the class, there are 3 boys. The ratio of girls to boys is 2:3.  Proportion is how much there is of one thing in relation to the whole amount. For example, there are 30 sweets in a bag. 1 in 5 of the sweets are red’.

The four main objectives listed in the National Curriculum are: • solve problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts • solve problems involving the calculation of percentages [for example, of measures such as 15% of 360 and the use of percentages for comparison] • solve problems involving similar shapes where the scale factor is known or can be found • solve problems involving unequal sharing and grouping using knowledge of fractions and multiples.

There are 40 sweets in a bag. There are 3 red sweets for every 5 orange sweets. How many red and orange sweets are there?  1. Work out the total number of parts.  For example, 3:5 is a total of 8 parts. 2. Find out how much one part is worth, by dividing by the total number of parts.  For example, if there are 40 sweets, split into a ratio of 3:5 red: orange sweets, 1 part would be 40÷8 = 5 3. Multiply each part of the ratio by the value of one part.  For example, red sweets: orange sweets = 3:5 1 part = 5  3 x 5 = 15 red sweets 5 x 5 = 25 orange sweets: 

DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn about the SATs revision programme or request a personalised quote from your school to speak to us about your school’s needs and how we can help.

Related articles

25 Year 6  Algebra Questions And Answers: KS2 Assessment Preparation

Year 6 Arithmetic Questions: 36 SATs-Style Questions and Answers

24 Fraction Questions For Year 6 (SATs): Complete With Answers

250+ SATs Questions Free To Download [With Answers]

FREE KS2 Maths SATs Practice Papers (Set of 6)

Get ready for KS2 SATs tests with this set of 6 maths SATs practice papers.

Includes 2 Arithmetic and 4 Reasoning Papers, with mark schemes and answer booklets, that follow the National Curriculum Assessments.

Privacy Overview

Module 1A: Problem Solving and Proportional Reasoning

Why it matters: problem solving and proportional reasoning, why understand the basics of problem solving, critical thinking.

Thinking comes naturally. You don’t have to make it happen—it just does. But you can make it happen in different ways. For example, you can think positively or negatively. You can think with “heart” and you can think with rational judgment. You can also think strategically and analytically, and mathematically and scientifically. These are a few of multiple ways in which the mind can process thought.

What are some forms of thinking you use? When do you use them, and why?

As a college student, you are tasked with engaging and expanding your thinking skills. One of the most important of these skills is critical thinking. Critical thinking is important because it relates to nearly all tasks, situations, topics, careers, environments, challenges, and opportunities. It’s a “domain-general” thinking skill—not a thinking skill that’s reserved for a one subject alone or restricted to a particular subject area.

Great leaders have highly attuned critical thinking skills, and you can, too. In fact, you probably have a lot of these skills already. Of all your thinking skills, critical thinking may have the greatest value.

What Is Critical Thinking?

Critical thinking is clear, reasonable, reflective thinking focused on deciding what to believe or do. It means asking probing questions like, “How do we know?” or “Is this true in every case or just in this instance?” It involves being skeptical and challenging assumptions, rather than simply memorizing facts or blindly accepting what you hear or read.

Who are critical thinkers, and what characteristics do they have in common? Critical thinkers are usually curious and reflective people. They like to explore and probe new areas and seek knowledge, clarification, and new solutions. They ask pertinent questions, evaluate statements and arguments, and they distinguish between facts and opinion. They are also willing to examine their own beliefs, possessing a manner of humility that allows them to admit lack of knowledge or understanding when needed. They are open to changing their mind. Perhaps most of all, they actively enjoy learning, and seeking new knowledge is a lifelong pursuit.

This may well be you!

The following video, from Lawrence Bland, presents the major concepts and benefits of critical thinking.

Critical Thinking and Logic

Critical thinking is fundamentally a process of questioning information and data. You may question the information you read in a textbook, or you may question what a politician or a professor or a classmate says. You can also question a commonly-held belief or a new idea. With critical thinking, anything and everything is subject to question and examination for the purpose of logically constructing reasoned perspectives.

Questions of Logic in Critical Thinking

Let’s use a simple example of applying logic to a critical-thinking situation. In this hypothetical scenario, a man has a PhD in political science, and he works as a professor at a local college. His wife works at the college, too. They have three young children in the local school system, and their family is well known in the community. The man is now running for political office. Are his credentials and experience sufficient for entering public office? Will he be effective in the political office? Some voters might believe that his personal life and current job, on the surface, suggest he will do well in the position, and they will vote for him. In truth, the characteristics described don’t guarantee that the man will do a good job. The information is somewhat irrelevant. What else might you want to know? How about whether the man had already held a political office and done a good job? In this case, we want to ask, How much information is adequate in order to make a decision based on logic instead of assumptions?

The following questions are ones you may apply to formulating a logical, reasoned perspective in the above scenario or any other situation:

• What’s happening? Gather the basic information and begin to think of questions.
• Why is it important? Ask yourself why it’s significant and whether or not you agree.
• What don’t I see? Is there anything important missing?
• How do I know? Ask yourself where the information came from and how it was constructed.
• Who is saying it? What’s the position of the speaker and what is influencing them?
• What else? What if? What other ideas exist and are there other possibilities?

Problem-Solving with Critical Thinking

For most people, a typical day is filled with critical thinking and problem-solving challenges. In fact, critical thinking and problem-solving go hand-in-hand. They both refer to using knowledge, facts, and data to solve problems effectively. But with problem-solving, you are specifically identifying, selecting, and defending your solution.

Problem-Solving Action Checklist

Problem-solving can be an efficient and rewarding process, especially if you are organized and mindful of critical steps and strategies. Remember, too, to assume the attributes of a good critical thinker. If you are curious, reflective, knowledge-seeking, open to change, probing, organized, and ethical, your challenge or problem will be less of a hurdle, and you’ll be in a good position to find intelligent solutions.

Critical Thinking, Problem Solving, and Math

In previous math courses, you’ve no doubt run into the infamous “word problems.” Unfortunately, these problems rarely resemble the type of problems we actually encounter in everyday life. In math books, you usually are told exactly which formula or procedure to use, and are given exactly the information you need to answer the question. In real life, problem solving requires identifying an appropriate formula or procedure, and determining what information you will need (and won’t need) to answer the question.

In this section, we will review several basic but powerful algebraic ideas: percents , rates , and proportions . We will then focus on the problem solving process, and explore how to use these ideas to solve problems where we don’t have perfect information.

• "Student Success-Thinking Critically In Class and Online."  Critical Thinking Gateway . St Petersburg College, n.d. Web. 16 Feb 2016. ↵
• Critical Thinking Skills. Authored by : Linda Bruce. Provided by : Lumen Learning. Located at : https://courses.lumenlearning.com/collegesuccess-lumen/chapter/critical-thinking-skills/ . Project : College Success. License : CC BY: Attribution
• Critical Thinking. Authored by : Critical and Creative Thinking Program. Located at : http://cct.wikispaces.umb.edu/Critical+Thinking . License : CC BY: Attribution
• Thinking Critically. Authored by : UBC Learning Commons. Provided by : The University of British Columbia, Vancouver Campus. Located at : http://www.oercommons.org/courses/learning-toolkit-critical-thinking/view . License : CC BY: Attribution
• Problem Solving. Authored by : David Lippman. Located at : http://www.opentextbookstore.com/mathinsociety/ . Project : Math in Society. License : CC BY-SA: Attribution-ShareAlike
• Critical Thinking.wmv. . Authored by : Lawrence Bland. Located at : https://youtu.be/WiSklIGUblo . License : All Rights Reserved . License Terms : Standard YouTube License

Privacy Policy