vector subtraction problem solving

Vector Subtraction

We can do vector subtraction just like how we do the subtraction of scalars. We subtract the corresponding components of vectors while subtracting vectors. The graphical interpretation of vector subtraction can be understood by using the parallelogram law and triangle law of addition.

Let us learn more about vector subtraction along with geometrical interpretation and examples.

What is Vector Subtraction?

The vector subtraction of two vectors a and b is represented by a - b and it is nothing but adding the negative of vector b to the vector a . i.e., a - b = a + (- b ). Thus, subtraction of vectors involves the addition of vectors and the negative of a vector. The result of vector subtraction is again a vector. The following are the rules for subtracting vectors:

• It should be performed between two vectors only (not between one vector and one scalar).
• Both vectors in the subtraction should represent the same physical quantity.

Let us understand how to subtract vectors graphically in the upcoming sections.

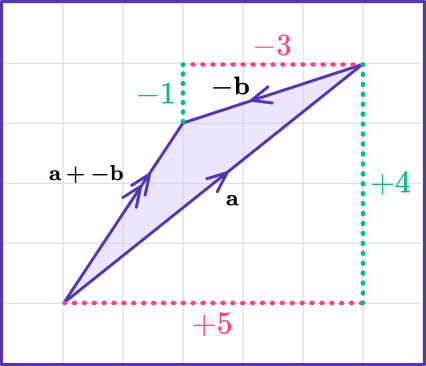
Vector Subtraction by Parallelogram Law

Suppose that a and b are two vectors . How can we interpret the subtraction of these vectors graphically? That is, what meaning do we attach to a - b ? To start with, we note that a - b will be a vector which when added to b should give back a . i.e.,

( a - b ) + b = a

But how do we determine the vector a - b , given the vectors a and b ? The following figure shows vectors a and b (we have drawn them to be co-initial ).

Using the parallelogram law of vector addition , we can determine the vector as follows. We interpret a - b as a + (- b ), that is, the vector sum of a and − b . Now, we reverse vector b , and then add a and - b using the parallelogram law:

This shows the vector subtraction a - b as the addition of a and − b .

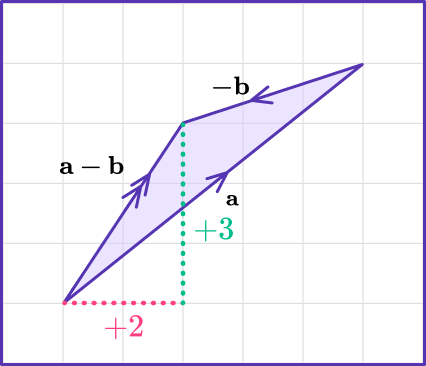
Vector Subtraction by Triangle Law

Now, we will interpret the subtraction of vectors using the triangle law of vector addition . Denote the vector drawn from the end-point of b to the end-point of a by c .

Note that b + c = a . Thus, c = a - b . In other words, the vector a - b is the vector drawn from the tip of b to the tip of a (if a and b are co-initial).

Note that both ways (using parallelogram law and triangle law) are described above give us the same vector for a - b . This becomes clearer from the figure below:

The vector PT is obtained by adding a and − b using the parallelogram law. The vector RQ is obtained by drawing the vector from the tip of b to the tip of - a . Clearly, both vectors are the same (as their magnitudes and directions are the same).

How to Subtract Vectors?

Here are multiple ways of subtracting vectors:

• To subtract two vectors a and b graphically (i.e., to find a - b ), just make them coinitial first and then draw a vector from the tip of b to the tip of a .
• We can add - b (the negative of vector b which is obtained by multiplying b with -1) to a to perform the vector subtraction a - b . i.e., a - b = a + ( -b ).
• If the vectors are in the component form we can just subtract their respective components in the order of subtraction of vectors. Here is an example.

Example: If a = <4, -2, 3> and b = <1, -2, 5> then find a - b .

a - b = <4, -2, 3> - <1, -2, 5>

= <4 - 1, -2 - (-2), 3 - 5>

= <3, 0, -2>

Therefore, a - b = <3, 0, -2>.

Properties of Vector Subtraction

Here are some important properties of vector subtraction.

• Any vector subtracted from itself results in a zero vector . i.e., a - a = 0 , for any vector a .
• The subtraction of vectors is NOT commutative . i.e., a - b is not necessarily equal to b - a.
• The vector subtraction is NOT associative. i.e., ( a - b ) - c does not need to be equal to a - ( b - c ).
• ( a - b ) · ( a + b ) = | a | 2 - | b | 2 .
• ( a - b ) · ( a - b ) = | a - b | 2 = | a | 2 + | b | 2 - 2 a · b .

☛ Related Topics:

• Types of Vectors
• Adding Vectors Calculator
• Vector Subtraction Calculator
• Angle Between Vectors

Vector Subtraction Examples

Example 1: Compute the vector subtraction a - b if a = <1, -2, 5> and b = <3, -1, 2>. Also, find its magnitude.

Given that a = <1, -2, 5> and b = <3, -1, 2>.

Now we will find their difference by subtracting the respective components.

a - b = <1, -2, 5> - <3, -1, 2> = <1 - 3, -2 - (-1), 5 - 2> = <-2, -1, 3>

Its magnitude is,

| a - b | = √[(-2) 2 + (-1) 2 + 3 2 ] = √(4 + 1 + 9) = √14

Answer: a - b = <-2, -1, 3> and its magnitude is √14.

Example 2: If θ is the angle between two unit vectors a and b , then find the magnitude of their difference in terms of θ.

From the properties of vector subtraction,

| a - b | 2 = | a | 2 + | b | 2 - 2 a · b ... (1)

By the definition of dot product ,

a · b = | a | | b | cos θ

Also, since a and b are unit vectors , | a | = | b | = 1.

Substituting these in (1):

| a - b | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ = 1 + 1 - 2 (1)(1) cos θ = 2 - 2 cos θ = 2 (1 - cos θ)

Using trig formulas, 1 - cos θ = 2 sin 2 (θ/2).

So | a - b | 2 = 2 (2 sin 2 (θ/2)) = 4 sin 2 (θ/2).

Taking square root,

| a - b | = 2 sin (θ/2).

Answer: | a - b | = 2 sin (θ/2).

Example 3: What can you say about two vectors a and b if the magnitudes of their sum and difference are equal to each other?

It is given that

| a - b | = | a + b |

Squaring on both sides,

| a - b | 2 = | a + b | 2

By the properties of vector subtraction,

| a | 2 + | b | 2 - 2 | a | | b | cos θ = | a | 2 + | b | 2 + 2 | a | | b | cos θ

4| a | | b | cos θ = 0

Answer: a and b are perpendicular.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Vector Subtraction

go to slide go to slide

FAQs on Vector Subtraction

What is meant by vector subtraction.

Vector subtraction of two vectors a and b is just the addition of vectors a and -b . i.e., a - b = a + (- b ). To find - b , we have to multiply each component of vector b by -1.

How Do You Subtract Vectors?

• To subtract a vector b from another vector a , just make them coinitial and then draw a vector from the tip of b to the tip of a .
• To subtract a vector b from another vector a when their components are given, then just subtract every component of b from the corresponding component of a .

How to Find Vector Difference Graphically?

To find the vector difference of two vectors a and b graphically:

• Draw both vectors to start from the same initial point.
• Draw the difference vector a - b from the tip of b to the tip of a .

How to Subtract Vectors in Component Form?

If two vectors are a = <a₁, a₂, a₃> and b = <b₁, b₂, b₃>, then their difference is represented by a - b and is obtained by subtracting components of b from the respective components of a . i.e., a - b = <a₁ - b₁, a₂ - b₂, a₃ - b₃>.

What is the Parallelogram Law of Vector Subtraction?

The parallelogram law of subtraction says "if two vectors a and -b are starting from a point P and they are two adjacent sides of a parallelogram , then their sum which is a + (- b ) (which can also be written as a - b ) is the vector that represents the diagonal of a parallelogram that starts from P".

What is the Triangle Law of Vector Subtraction?

The triangle law of vector subtraction says "to find the difference a - b of two vectors a and b (that are coinitial), just draw a vector from the tail of b to the tail of a ".

Vector Subtraction

In these lessons, we will learn how to subtract vectors by adding its negative, how to subtract vectors geometrically using the head-to-tail method and how to subtract vectors using their components.

Related Pages Vectors Equal Vectors Vector Addition Vector Multiplication Vector Geometry

What is a vector? A vector is a quantity that has magnitude (size) and direction.

How to represent a vector graphically, in column-vector form and in unit-vector form?

How to subtract Vectors?

The following diagram shows how to subtract vectors graphically. Scroll down the page for more examples and solutions for vector subtraction.

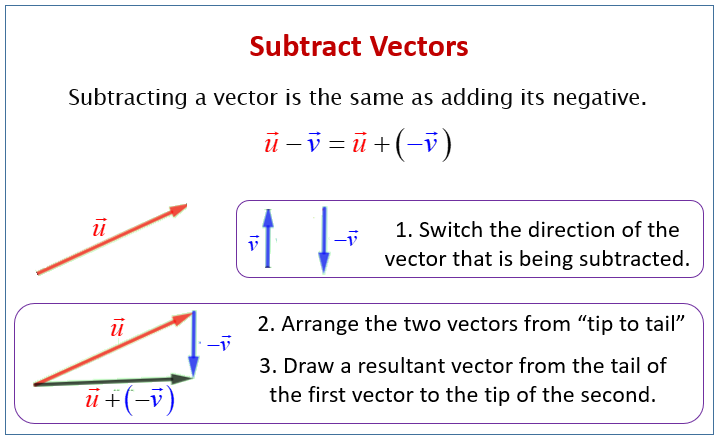
Subtracting a vector is the same as adding its negative. The difference of the vectors p and q is the sum of p and – q . p – q = p + (– q )

Example: Subtract the vector v from the vector u .

u – v = u + (– v )

Change the direction of vector v to get the vector – v .

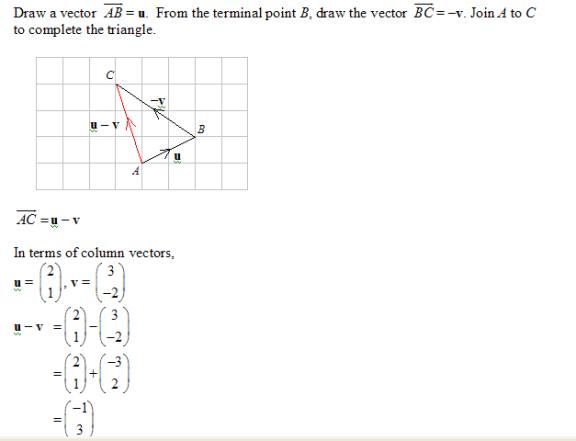
Check: The column vector should represent the vector that was drawn.

How to subtract vectors using column vectors? u - v = u + (-v) Since we know how to add vectors and multiply by negative one, we can also subtract vectors.

How to subtract vectors using column vectors and explained graphically?

How to subtract vectors graphically?

Geometric subtraction of two vectors

How to solve word problems using vector subtraction? Vector word problems when given magnitude and direction Subtract the following vectors (B - A) A = 5.0 m at 40 degrees west of North B = 2.5 m south. Find the distance and direction of (B - A)

Vector subtraction including boat example Introduction to ‘head to tail’ vector subtraction in the geometric sense. This is then applied to an example of working out a boat’s velocity relative to water given the velocity of the current and the velocity of the boat relative to land are both known. velocity relative to land = water velocity + boat’s velocity relative to water.

Example: A woman wants to get to a destination that is due North of her starting point. To do this, she needs to row across a stream. The current is flowing East at 12km/hr. The woman can row the boat at a constant speed of 16km/hr. What will be the required direction that she must row the boat in order to reach the required destination?

How to subtract vectors using their components

Subtracting Vectors in Component Form for 2-D and 3-D vectors.

How to add and subtract vectors in component form?

Example: Let u = <-1, 3>, v = <2, 4>, and w = <2, -5>. Find the component form of the vector u + v u - w 2u + 3w 2u - 4v -2u - 3v

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

Negative numbers

Vector notation

Column vectors

Vector addition

Subtracting vectors

Here you will learn about vector subtraction, including representing subtracting vectors graphically and understanding the subtraction of vectors as magnitude.

Students will first learn about the subtraction of vectors as a part of Vector and Matrix Quantities in high school mathematics.

What is vector subtraction?

Vector subtraction is subtracting one vector from another vector.

To do this, subtract the horizontal components (top numbers) of the column vector and subtract the vertical components (bottom numbers) of the column vector.

For example, look at vector \mathbf{a} and vector \mathbf{b}.

Subtracting vectors is based on the addition of vectors. The first vector stays the same, but the second vector reverses to the opposite direction to become a negative vector. Using the inverse allows you to change vector subtraction to vector addition.

Using vector \mathbf{a} and vector \mathbf{b}, let’s see what happens.

The direction of the vector \mathbf{-b} is opposite to the direction of the original vector \mathbf{b}, but has the same magnitude of the resultant vector, or distance from the initial point or starting point.

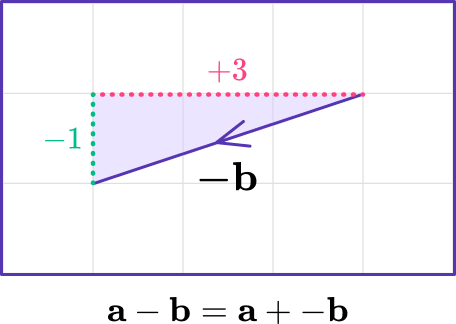
You know from vector addition that when adding two vectors, you add the second on to the end of the first, as shown below.

The final answer is known as the resultant vector or new vector.

Common Core State Standards

How does this relate to high school math?

• High School: Number and Quantity: Vector and Matrix Quantities (HSN.VM.B.4) Understand vector subtraction v-w as v + (-w), where -w is the additive inverse of w, with the same magnitude as w and pointing in the opposite direction. Represent vector subtraction graphically by connecting the tips in the appropriate order, and perform vector subtraction component-wise.

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

How to subtract vectors

In order to subtract a vector from an original vector:

Subtract the \textbf{x} components.

Subtract the \textbf{y} components.

Write the resultant vector.

Vector subtraction examples

Example 1: subtract vectors.

Subtract the vectors below.

Subtract the second top number from the first top number.

2 Subtract the \textbf{y} components.

Subtract the second bottom number from the first bottom number.

3 Write the resultant vector.

Write the two answers as a column vector.

Example 2: subtract vectors

\left(\begin{aligned} 3\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} 5\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} -2\\ 1\\ \end{aligned}\right)

Example 3: subtract vectors

Example 4: subtract vectors.

\left(\begin{aligned} -4\\ 3\\ \end{aligned}\right) -\ \left(\begin{aligned} 2\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} -6\\ 2\\ \end{aligned}\right)

Example 5: subtract vectors

\left(\begin{aligned} -5\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} -3\\ -2\\ \end{aligned}\right) =\ \left(\begin{aligned} -2\\ 4\\ \end{aligned}\right)

Example 6: subtract vectors

Teaching tips for subtracting vectors.

• Encourage students to visualize vector subtraction using diagrams or geometric representations. This helps them understand the concept of subtracting one vector from another, considering both magnitude and direction of the arrowhead. Drawing vectors on a coordinate system can aid in visualizing the process. Have students draw the x -axis and y -axis and utilize prior knowledge to help them visualize the components of vectors.
• Teach the head-to-tail method for vector subtraction. In this method, place the tail of the second vector at the head of the first vector, and the resulting vector goes from the tail of the first vector to the head of the second vector. Emphasize the importance of maintaining the order of subtraction for accurate results, as the commutative property does not apply to vector subtraction.
• Break down vectors into their components (horizontal and vertical) and teach students to subtract corresponding components separately. This method is particularly useful when working with vectors in two-dimensional space. After subtracting components, guide students to combine the results to obtain the resultant vector.
• Provide real-world examples and word problems that involve vector subtraction. This helps students connect the mathematical concept to practical scenarios. Use scenarios such as a displacement vector, velocity, or force vectors to make the learning experience more engaging and applicable. Draw on student knowledge of trigonometry, the pythagorean theorem and geometric figures like parallelograms to help their understanding.

Easy mistakes to make

• Ignoring direction One common mistake is neglecting the directional aspect of vectors. Students may focus solely on the magnitudes and forget that vectors have both magnitude and direction. Emphasize the importance of the direction of the resultant when subtracting vectors to avoid this error.
• Confusing head-to-tail order In the head-to-tail method, the order of subtraction matters. Prompt students to recall that subtraction is not commutative. Students might inadvertently reverse the order of vectors, leading to incorrect results. Remind them to maintain the correct order to ensure accurate vector subtraction.
• Component confusion Misunderstanding vector components is another common mistake. Students might confuse horizontal and vertical components or mix up the signs when subtracting. Reinforce the concept of breaking down vectors into components and subtracting them separately to minimize this error.
• Forgetting negative vectors Since vector subtraction is equivalent to adding the negative of a vector, students may forget to include the negative sign when subtracting. Remind them to pay attention to signs and clarify the connection between subtraction and the addition of negative vectors.
• Skipping visualization Students may skip the visualization step and attempt to subtract vectors algebraically without understanding the geometric representation using the coordinate system. Encourage them to draw diagrams or use graphical aids to visualize the initial endpoint, the length of the arrow, and the magnitude of a vector, helping to prevent errors related to misinterpretation.

Related vector lessons

• Vector multiplication
• Adding vectors
• Component form of a vector
• Vector practice problems
• Magnitude of a vector

Practice vector subtraction questions

1) Work out \textbf{v}-\textbf{w} :

2) Work out \textbf{c}-\textbf{d} :

3) Work out \textbf{b}-\textbf{a} :

4) Work out \textbf{p}-\textbf{q} :

5) Work out \textbf{s}-\textbf{r} :

6) Work out \textbf{e}-\textbf{d} :

Subtracting vectors FAQs

Vector subtraction using the head-to-tail method involves placing the tail of the second vector at the head of the first vector. The resultant vector then goes from the tail of the first vector to the head of the second vector. It’s crucial to maintain the correct order to ensure precise results in vector operations.

Common mistakes in vector subtraction include neglecting vector direction, confusing the head-to-tail order, misunderstanding vector components, and forgetting to account for negative vectors. Visualization and careful attention to these aspects help prevent errors and ensure accurate results in vector mathematics.

Yes, vector subtraction can be simplified by breaking it into components. By decomposing vectors into horizontal and vertical components, students can subtract corresponding components separately. This method aids in clarity and accuracy when performing vector subtraction in two-dimensional space.

Vector subtraction is equivalent to adding the negative of a vector. When subtracting a vector, you can achieve the same result by adding its negative and finding the vector sum. Paying attention to signs and understanding this relationship simplifies vector operations and provides a conceptual bridge between vector addition and subtraction.

The next lessons are

• Trig graphs
• Quadratic equations
• Functions in algebra

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

3.3 Vector Addition and Subtraction: Analytical Methods

Learning objectives.

By the end of this section, you will be able to:

• Understand the rules of vector addition and subtraction using analytical methods.
• Apply analytical methods to determine vertical and horizontal component vectors.
• Apply analytical methods to determine the magnitude and direction of a resultant vector.

Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.

Resolving a Vector into Perpendicular Components

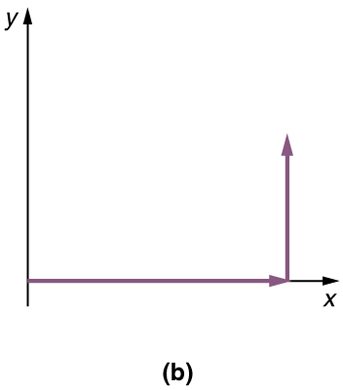
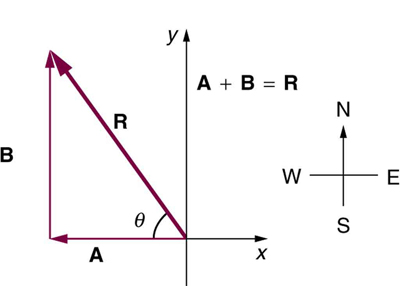
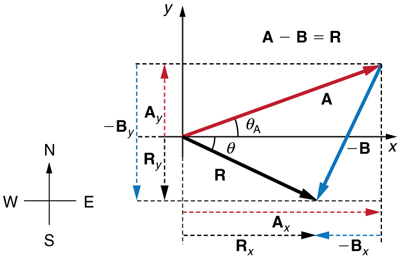
Analytical techniques and right triangles go hand-in-hand in physics because (among other things) motions along perpendicular directions are independent. We very often need to separate a vector into perpendicular components. For example, given a vector like A A in Figure 3.24 , we may wish to find which two perpendicular vectors, A x A x and A y A y , add to produce it.

A x A x and A y A y are defined to be the components of A A along the x - and y -axes. The three vectors A A , A x A x , and A y A y form a right triangle:

Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). The relationship does not apply for the magnitudes alone. For example, if A x = 3 m A x = 3 m east, A y = 4 m A y = 4 m north, and A = 5 m A = 5 m north-east, then it is true that the vectors A x  + A y  = A A x  + A y  = A . However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,

If the vector A A is known, then its magnitude A A (its length) and its angle θ θ (its direction) are known. To find A x A x and A y A y , its x - and y -components, we use the following relationships for a right triangle.

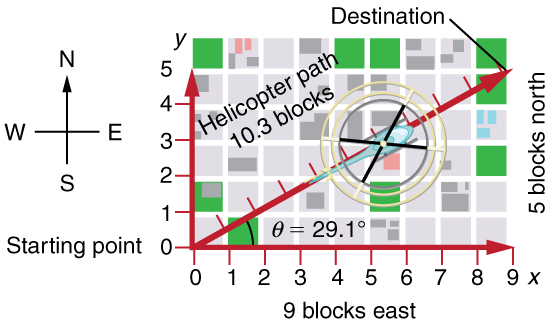
Suppose, for example, that A A is the vector representing the total displacement of the person walking in a city considered in Kinematics in Two Dimensions: An Introduction and Vector Addition and Subtraction: Graphical Methods .

Then A = 10.3 A = 10.3 blocks and θ = 29.1º θ = 29.1º , so that

Calculating a Resultant Vector

If the perpendicular components A x A x and A y A y of a vector A A are known, then A A can also be found analytically. To find the magnitude A A and direction θ θ of a vector from its perpendicular components A x A x and A y A y , relative to the x -axis, we use the following relationships:

Note that the equation A = A x 2 + A y 2 A = A x 2 + A y 2 is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if A x A x and A y A y are 9 and 5 blocks, respectively, then A = 9 2 +5 2 =10 . 3 A = 9 2 +5 2 =10 . 3 blocks, again consistent with the example of the person walking in a city. Finally, the direction is θ = tan –1 ( 5/9 ) =29.1º θ = tan –1 ( 5/9 ) =29.1º , as before.

Determining Vectors and Vector Components with Analytical Methods

Equations A x = A cos θ A x = A cos θ and A y = A sin θ A y = A sin θ are used to find the perpendicular components of a vector—that is, to go from A A and θ θ to A x A x and A y A y . Equations A = A x 2 + A y 2 A = A x 2 + A y 2 and θ = tan –1 ( A y / A x ) θ = tan –1 ( A y / A x ) are used to find a vector from its perpendicular components—that is, to go from A x A x and A y A y to A A and θ θ . Both processes are crucial to analytical methods of vector addition and subtraction.

Adding Vectors Using Analytical Methods

To see how to add vectors using perpendicular components, consider Figure 3.28 , in which the vectors A A and B B are added to produce the resultant R R .

If A A and B B represent two legs of a walk (two displacements), then R R is the total displacement. The person taking the walk ends up at the tip of R . R . There are many ways to arrive at the same point. In particular, the person could have walked first in the x -direction and then in the y -direction. Those paths are the x - and y -components of the resultant, R x R x and R y R y . If we know R x R x and R y R y , we can find R R and θ θ using the equations A = A x 2 + A y 2 A = A x 2 + A y 2 and θ = tan –1 ( A y / A x ) θ = tan –1 ( A y / A x ) . When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.

Step 1. Identify the x- and y-axes that will be used in the problem. Then, find the components of each vector to be added along the chosen perpendicular axes . Use the equations A x = A cos θ A x = A cos θ and A y = A sin θ A y = A sin θ to find the components. In Figure 3.29 , these components are A x A x , A y A y , B x B x , and B y B y . The angles that vectors A A and B B make with the x -axis are θ A θ A and θ B θ B , respectively.

Step 2. Find the components of the resultant along each axis by adding the components of the individual vectors along that axis . That is, as shown in Figure 3.30 ,

Components along the same axis, say the x -axis, are vectors along the same line and, thus, can be added to one another like ordinary numbers. The same is true for components along the y -axis. (For example, a 9-block eastward walk could be taken in two legs, the first 3 blocks east and the second 6 blocks east, for a total of 9, because they are along the same direction.) So resolving vectors into components along common axes makes it easier to add them. Now that the components of R R are known, its magnitude and direction can be found.

Step 3. To get the magnitude R R of the resultant, use the Pythagorean theorem:

Step 4. To get the direction of the resultant relative to the x -axis:

The following example illustrates this technique for adding vectors using perpendicular components.

Example 3.3

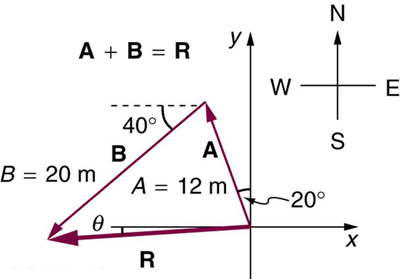
Add the vector A A to the vector B B shown in Figure 3.31 , using perpendicular components along the x - and y -axes. The x - and y -axes are along the east–west and north–south directions, respectively. Vector A A represents the first leg of a walk in which a person walks 53 . 0 m 53 . 0 m in a direction 20 . 0 º 20 . 0 º north of east. Vector B B represents the second leg, a displacement of 34 . 0 m 34 . 0 m in a direction 63 . 0 º 63 . 0 º north of east.

The components of A A and B B along the x - and y -axes represent walking due east and due north to get to the same ending point. Once found, they are combined to produce the resultant.

Following the method outlined above, we first find the components of A A and B B along the x - and y -axes. Note that A = 53.0 m A = 53.0 m , θ A = 20.0º θ A = 20.0º , B = 34.0 m B = 34.0 m , and θ B = 63.0º θ B = 63.0º . We find the x -components by using A x = A cos θ A x = A cos θ , which gives

Similarly, the y -components are found using A y = A sin θ A A y = A sin θ A :

The x - and y -components of the resultant are thus

Now we can find the magnitude of the resultant by using the Pythagorean theorem:

Finally, we find the direction of the resultant:

This example illustrates the addition of vectors using perpendicular components. Vector subtraction using perpendicular components is very similar—it is just the addition of a negative vector.

Subtraction of vectors is accomplished by the addition of a negative vector. That is, A − B ≡ A + ( –B ) A − B ≡ A + ( –B ) . Thus, the method for the subtraction of vectors using perpendicular components is identical to that for addition . The components of –B –B are the negatives of the components of B B . The x - and y -components of the resultant A − B = R A − B = R are thus

and the rest of the method outlined above is identical to that for addition. (See Figure 3.33 .)

Analyzing vectors using perpendicular components is very useful in many areas of physics, because perpendicular quantities are often independent of one another. The next module, Projectile Motion , is one of many in which using perpendicular components helps make the picture clear and simplifies the physics.

PhET Explorations

Vector addition.

Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/3-3-vector-addition-and-subtraction-analytical-methods

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

3 Two-dimensional Kinematics

17 3.2 Vector Addition and Subtraction: Graphical Methods

• Understand the rules of vector addition, subtraction, and multiplication.
• Apply graphical methods of vector addition and subtraction to determine the displacement of moving objects.

Vectors in Two Dimensions

A vector is a quantity that has magnitude and direction. Displacement, velocity, acceleration, and force, for example, are all vectors. In one-dimensional, or straight-line, motion, the direction of a vector can be given simply by a plus or minus sign. In two dimensions (2-d), however, we specify the direction of a vector relative to some reference frame (i.e., coordinate system), using an arrow having length proportional to the vector’s magnitude and pointing in the direction of the vector.

Figure 2 shows such a graphical representation of a vector , using as an example the total displacement for the person walking in a city considered in Chapter 3.1 Kinematics in Two Dimensions: An Introduction . We shall use the notation that a boldface symbol, such as[latex]\textbf{D}[/latex], stands for a vector. Its magnitude is represented by the symbol in italics,[latex]\boldsymbol{D},[/latex]and its direction by[latex]\boldsymbol{\theta}.[/latex]

VECTORS IN THIS TEXT

In this text, we will represent a vector with a boldface variable. For example, we will represent the quantity force with the vector[latex]\textbf{F},[/latex]which has both magnitude and direction. The magnitude of the vector will be represented by a variable in italics, such as[latex]\boldsymbol{F},[/latex]and the direction of the variable will be given by an angle[latex]\boldsymbol{\theta}.[/latex]

Vector Addition: Head-to-Tail Method

The head-to-tail method is a graphical way to add vectors, described in Figure 4 below and in the steps following. The tail of the vector is the starting point of the vector, and the head (or tip) of a vector is the final, pointed end of the arrow.

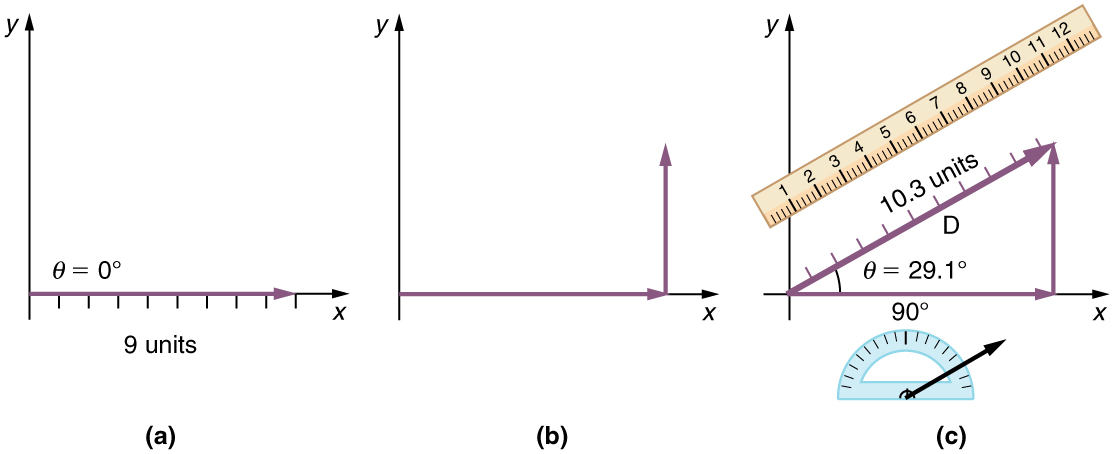
Step 1. Draw an arrow to represent the first vector (9 blocks to the east) using a ruler and protractor .

Step 2. Now draw an arrow to represent the second vector (5 blocks to the north). Place the tail of the second vector at the head of the first vector .

Step 3. If there are more than two vectors, continue this process for each vector to be added. Note that in our example, we have only two vectors, so we have finished placing arrows tip to tail .

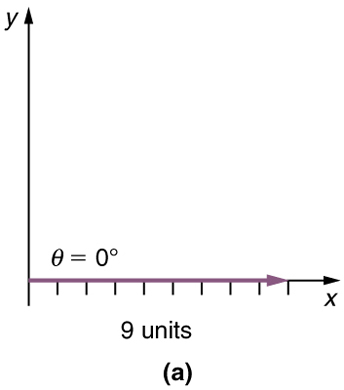
Step 4. Draw an arrow from the tail of the first vector to the head of the last vector . This is the resultant , or the sum, of the other vectors.

Step 5. To get the magnitude of the resultant, measure its length with a ruler. (Note that in most calculations, we will use the Pythagorean theorem to determine this length.)

Step 6. To get the direction of the resultant, measure the angle it makes with the reference frame using a protractor. (Note that in most calculations, we will use trigonometric relationships to determine this angle.)

The graphical addition of vectors is limited in accuracy only by the precision with which the drawings can be made and the precision of the measuring tools. It is valid for any number of vectors.

Example 1: Adding Vectors Graphically Using the Head-to-Tail Method: A Women Takes a Walk

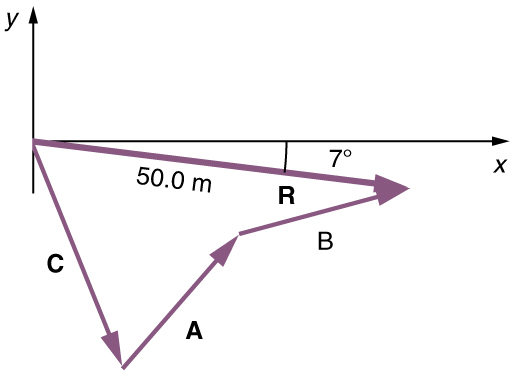
Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction[latex]\boldsymbol{49.0^o}[/latex]north of east. Then, she walks 23.0 m heading[latex]\boldsymbol{15.0^o}[/latex]north of east. Finally, she turns and walks 32.0 m in a direction 68.0° south of east.

Represent each displacement vector graphically with an arrow, labeling the first[latex]\textbf{A},[/latex]the second[latex]\textbf{B},[/latex]and the third[latex]\textbf{C},[/latex]making the lengths proportional to the distance and the directions as specified relative to an east-west line. The head-to-tail method outlined above will give a way to determine the magnitude and direction of the resultant displacement, denoted[latex]\textbf{R}.[/latex]

(1) Draw the three displacement vectors.

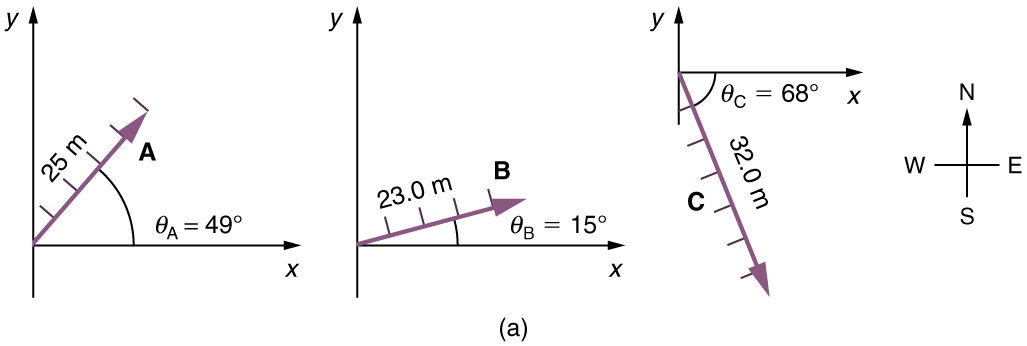
(2) Place the vectors head to tail retaining both their initial magnitude and direction.

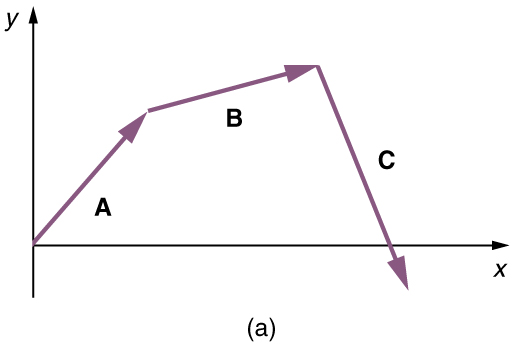
(3) Draw the resultant vector,[latex]\textbf{R}.[/latex]

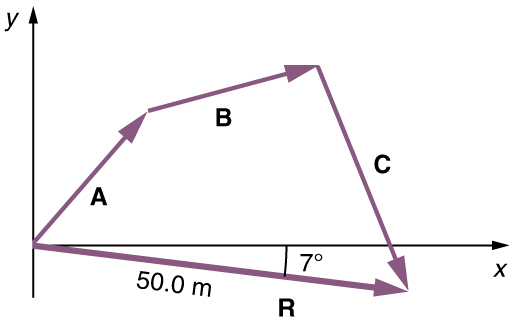
(4) Use a ruler to measure the magnitude of[latex]\textbf{R},[/latex]and a protractor to measure the direction of[latex]\textbf{R}.[/latex]While the direction of the vector can be specified in many ways, the easiest way is to measure the angle between the vector and the nearest horizontal or vertical axis. Since the resultant vector is south of the eastward pointing axis, we flip the protractor upside down and measure the angle between the eastward axis and the vector.

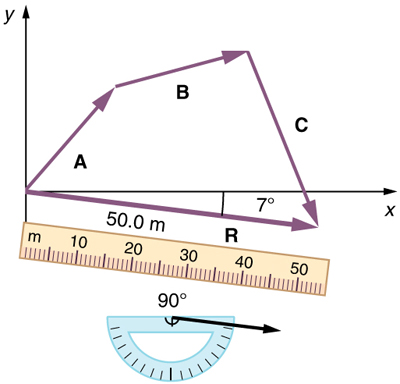
In this case, the total displacement[latex]\textbf{R}[/latex]is seen to have a magnitude of 50.0 m and to lie in a direction[latex]\boldsymbol{7.0^o}[/latex]south of east. By using its magnitude and direction, this vector can be expressed as[latex]\boldsymbol{\textbf{R}=50.0\textbf{ m}}[/latex]and[latex]\boldsymbol{\theta=7.0^o}[/latex]south of east.

The head-to-tail graphical method of vector addition works for any number of vectors. It is also important to note that the resultant is independent of the order in which the vectors are added. Therefore, we could add the vectors in any order as illustrated in Figure 12 and we will still get the same solution.

Here, we see that when the same vectors are added in a different order, the result is the same. This characteristic is true in every case and is an important characteristic of vectors. Vector addition is commutative . Vectors can be added in any order.

(This is true for the addition of ordinary numbers as well—you get the same result whether you add[latex]\boldsymbol{2+3}[/latex]or[latex]\boldsymbol{3+2},[/latex]for example).

Vector Subtraction

Vector subtraction is a straightforward extension of vector addition. To define subtraction (say we want to subtract[latex]\textbf{B}[/latex]from[latex]\textbf{A},[/latex]written[latex]\boldsymbol{\textbf{A}-\textbf{B}}[/latex], we must first define what we mean by subtraction. The negative of a vector[latex]\textbf{B}[/latex]is defined to be[latex]\boldsymbol{-\textbf{B}};[/latex]that is, graphically the negative of any vector has the same magnitude but the opposite direction , as shown in Figure 13 . In other words,[latex]\textbf{B}[/latex]has the same length as[latex]\boldsymbol{-\textbf{B}},[/latex]but points in the opposite direction. Essentially, we just flip the vector so it points in the opposite direction.

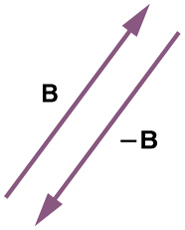
The subtraction of vector[latex]\textbf{B}[/latex]from vector[latex]\textbf{A}[/latex]is then simply defined to be the addition of[latex]\boldsymbol{-\textbf{B}}[/latex]to[latex]\textbf{A}.[/latex]Note that vector subtraction is the addition of a negative vector. The order of subtraction does not affect the results.

This is analogous to the subtraction of scalars (where, for example,[latex]\boldsymbol{5-2=5+(-2)}[/latex]). Again, the result is independent of the order in which the subtraction is made. When vectors are subtracted graphically, the techniques outlined above are used, as the following example illustrates.

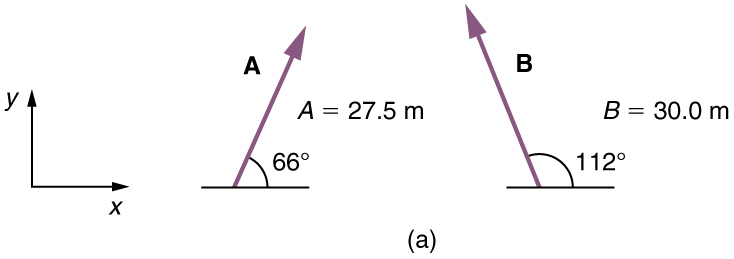
Example 2: Subtracting Vectors Graphically: A Women Sailing a Boat

A woman sailing a boat at night is following directions to a dock. The instructions read to first sail 27.5 m in a direction[latex]\boldsymbol{66.0^o}[/latex]north of east from her current location, and then travel 30.0 m in a direction[latex]\boldsymbol{112^o}[/latex]north of east (or[latex]\boldsymbol{22.0^o}[/latex]west of north). If the woman makes a mistake and travels in the opposite direction for the second leg of the trip, where will she end up? Compare this location with the location of the dock.

We can represent the first leg of the trip with a vector[latex]\textbf{A},[/latex]and the second leg of the trip with a vector[latex]\textbf{B}.[/latex]The dock is located at a location[latex]\boldsymbol{\textbf{A}\:+\:\textbf{B}}.[/latex]If the woman mistakenly travels in the opposite direction for the second leg of the journey, she will travel a distance[latex]\textbf{B}[/latex](30.0 m) in the direction[latex]\boldsymbol{180^o-112^o=68^o}[/latex]south of east. We represent this as[latex]\boldsymbol{-\textbf{B}},[/latex]as shown below. The vector[latex]\boldsymbol{-\textbf{B}}[/latex]has the same magnitude as[latex]\textbf{B}[/latex]but is in the opposite direction. Thus, she will end up at a location[latex]\boldsymbol{\textbf{A}+(-\textbf{B})},[/latex]or[latex]\boldsymbol{\textbf{A}-\textbf{B}}.[/latex]

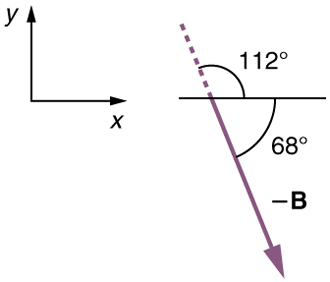
We will perform vector addition to compare the location of the dock,[latex]\boldsymbol{\textbf{A}+\textbf{B}},[/latex]with the location at which the woman mistakenly arrives,[latex]\boldsymbol{\textbf{A}+(-\textbf{B})}.[/latex]

(1) To determine the location at which the woman arrives by accident, draw vectors[latex]\textbf{A}[/latex]and[latex]\boldsymbol{-\textbf{B}}.[/latex]

(2) Place the vectors head to tail.

(3) Draw the resultant vector[latex]\textbf{R}.[/latex]

(4) Use a ruler and protractor to measure the magnitude and direction of[latex]\textbf{R}.[/latex]

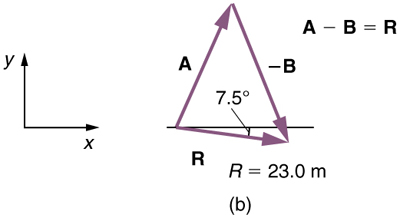
In this case,[latex]\boldsymbol{\textbf{R}=23.0\textbf{ m}}[/latex]and[latex]\boldsymbol{\theta=7.5^o}[/latex]south of east.

(5) To determine the location of the dock, we repeat this method to add vectors[latex]\textbf{A}[/latex]and[latex]\textbf{B}.[/latex]We obtain the resultant vector[latex]\boldsymbol{\textbf{R}^{\prime}:}[/latex]

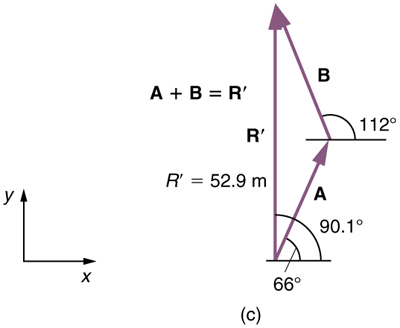
In this case[latex]\boldsymbol{\textbf{R}=52.9\textbf{ m}}[/latex]and[latex]\boldsymbol{\theta=90.1^o}[/latex]north of east.

We can see that the woman will end up a significant distance from the dock if she travels in the opposite direction for the second leg of the trip.

Because subtraction of a vector is the same as addition of a vector with the opposite direction, the graphical method of subtracting vectors works the same as for addition.

Multiplication of Vectors and Scalars

If we decided to walk three times as far on the first leg of the trip considered in the preceding example, then we would walk[latex]\boldsymbol{3 \times 27.5\textbf{ m}},[/latex]or 82.5 m, in a direction[latex]\boldsymbol{66.0^o}[/latex]north of east. This is an example of multiplying a vector by a positive scalar . Notice that the magnitude changes, but the direction stays the same.

If the scalar is negative, then multiplying a vector by it changes the vector’s magnitude and gives the new vector the opposite direction. For example, if you multiply by –2, the magnitude doubles but the direction changes. We can summarize these rules in the following way: When vector[latex]\textbf{A}[/latex]is multiplied by a scalar[latex]\boldsymbol{c},[/latex]

• the magnitude of the vector becomes the absolute value of[latex]\boldsymbol{cA},[/latex]
• if[latex]\boldsymbol{c}[/latex]is positive, the direction of the vector does not change,
• if[latex]\boldsymbol{c}[/latex]is negative, the direction is reversed.

In our case,[latex]\boldsymbol{c=3}[/latex]and[latex]\boldsymbol{\textbf{A}=27.5\textbf{ m}}.[/latex]Vectors are multiplied by scalars in many situations. Note that division is the inverse of multiplication. For example, dividing by 2 is the same as multiplying by the value (1/2). The rules for multiplication of vectors by scalars are the same for division; simply treat the divisor as a scalar between 0 and 1.

Resolving a Vector into Components

In the examples above, we have been adding vectors to determine the resultant vector. In many cases, however, we will need to do the opposite. We will need to take a single vector and find what other vectors added together produce it. In most cases, this involves determining the perpendicular components of a single vector, for example the x – and y -components, or the north-south and east-west components.

For example, we may know that the total displacement of a person walking in a city is 10.3 blocks in a direction[latex]\boldsymbol{29.0^o}[/latex]north of east and want to find out how many blocks east and north had to be walked. This method is called finding the components (or parts) of the displacement in the east and north directions, and it is the inverse of the process followed to find the total displacement. It is one example of finding the components of a vector. There are many applications in physics where this is a useful thing to do. We will see this soon in Chapter 3.4 Projectile Motion , and much more when we cover forces in Chapter 4 Dynamics: Newton’s Laws of Motion . Most of these involve finding components along perpendicular axes (such as north and east), so that right triangles are involved. The analytical techniques presented in Chapter 3.3 Vector Addition and Subtraction: Analytical Methods are ideal for finding vector components.

PHET EXPLORATIONS: MAZE GAME

Learn about position, velocity, and acceleration in the “Arena of Pain”. Use the green arrow to move the ball. Add more walls to the arena to make the game more difficult. Try to make a goal as fast as you can.

• The graphical method of adding vectors [latex]\textbf{A}[/latex]and[latex]\textbf{B}[/latex]involves drawing vectors on a graph and adding them using the head-to-tail method. The resultant vector[latex]\textbf{R}[/latex]is defined such that[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]The magnitude and direction of[latex]\textbf{R}[/latex]are then determined with a ruler and protractor, respectively.
• The graphical method of subtracting vector [latex]\textbf{B}[/latex]from[latex]\textbf{A}[/latex]involves adding the opposite of vector[latex]\textbf{B},[/latex]which is defined as[latex]\boldsymbol{-\textbf{B}}.[/latex]In this case,[latex]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A}+(-\textbf{B})=\textbf{R}}.[/latex]Then, the head-to-tail method of addition is followed in the usual way to obtain the resultant vector[latex]\textbf{R}.[/latex]
• Addition of vectors is commutative such that[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
• The head-to-tail method of adding vectors involves drawing the first vector on a graph and then placing the tail of each subsequent vector at the head of the previous vector. The resultant vector is then drawn from the tail of the first vector to the head of the final vector.
• If a vector[latex]\textbf{A}[/latex]is multiplied by a scalar quantity[latex]\boldsymbol{c},[/latex]the magnitude of the product is given by[latex]\boldsymbol{cA}.[/latex]If[latex]\boldsymbol{c}[/latex]is positive, the direction of the product points in the same direction as[latex]\textbf{A};[/latex]if[latex]\boldsymbol{c}[/latex]is negative, the direction of the product points in the opposite direction as[latex]\textbf{A}.[/latex]

Conceptual Questions

1: Which of the following is a vector: a person’s height, the altitude on Mt. Everest, the age of the Earth, the boiling point of water, the cost of this book, the Earth’s population, the acceleration of gravity?

2: Give a specific example of a vector, stating its magnitude, units, and direction.

3: What do vectors and scalars have in common? How do they differ?

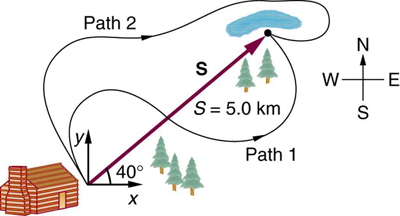
4: Two campers in a national park hike from their cabin to the same spot on a lake, each taking a different path, as illustrated below. The total distance traveled along Path 1 is 7.5 km, and that along Path 2 is 8.2 km. What is the final displacement of each camper?

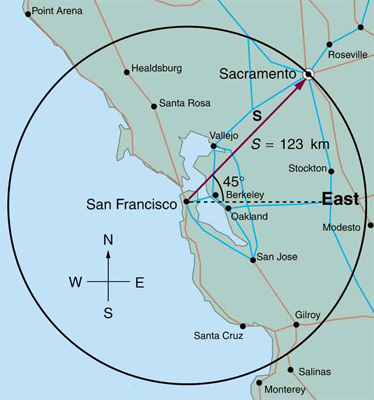
5: If an airplane pilot is told to fly 123 km in a straight line to get from San Francisco to Sacramento, explain why he could end up anywhere on the circle shown in Figure 20 . What other information would he need to get to Sacramento?

6: Suppose you take two steps[latex]\textbf{A}[/latex]and[latex]\textbf{B}[/latex](that is, two nonzero displacements). Under what circumstances can you end up at your starting point? More generally, under what circumstances can two nonzero vectors add to give zero? Is the maximum distance you can end up from the starting point[latex]\boldsymbol{\textbf{A}+\textbf{B}}[/latex]the sum of the lengths of the two steps?

7: Explain why it is not possible to add a scalar to a vector.

8:  If you take two steps of different sizes, can you end up at your starting point? More generally, can two vectors with different magnitudes ever add to zero? Can three or more?

Problems & Exercises

Use graphical methods to solve these problems. You may assume data taken from graphs is accurate to three digits.

1: Find the following for path A in Figure 21 : (a) the total distance traveled, and (b) the magnitude and direction of the displacement from start to finish.

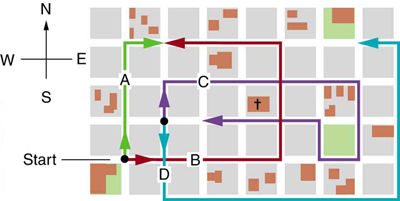
2: Find the following for path B in Figure 21 : (a) the total distance traveled, and (b) the magnitude and direction of the displacement from start to finish.

3: Find the north and east components of the displacement for the hikers shown in Figure 19 .

4: Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements[latex]\textbf{A}[/latex]and[latex]\textbf{B},[/latex]as in Figure 22 , then this problem asks you to find their sum[latex]\boldsymbol{\textbf{R}=\textbf{A}+\textbf{B}}[/latex].)

5: Suppose you first walk 12.0 m in a direction[latex]\boldsymbol{20^o}[/latex]west of north and then 20.0 m in a direction[latex]\boldsymbol{40.0^o}[/latex]south of west. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements[latex]\textbf{A}[/latex]and[latex]\textbf{B},[/latex]as in Figure 23 , then this problem finds their sum[latex]\boldsymbol{\textbf{R} =\textbf{A} +\textbf{B}}[/latex].)

6: Repeat the problem above, but reverse the order of the two legs of the walk; show that you get the same final result. That is, you first walk leg[latex]\textbf{B},[/latex]which is 20.0 m in a direction exactly[latex]\boldsymbol{40^o}[/latex]south of west, and then leg[latex]\textbf{A},[/latex] which is 12.0 m in a direction exactly[latex]\boldsymbol{20^o}[/latex]west of north. (This problem shows that[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex])

7: (a) Repeat the problem two problems prior, but for the second leg you walk 20.0 m in a direction[latex]\boldsymbol{40.0^o}[/latex]north of east (which is equivalent to subtracting[latex]\textbf{B}[/latex]from[latex]\textbf{A}[/latex] —that is, to finding[latex]\boldsymbol{\textbf{R}^{\prime}=\textbf{A}-\textbf{B}}[/latex]). (b) Repeat the problem two problems prior, but now you first walk 20.0 m in a direction[latex]\boldsymbol{40.0^o}[/latex]south of west and then 12.0 m in a direction[latex]\boldsymbol{20.0^o}[/latex]east of south (which is equivalent to subtracting[latex]\textbf{A}[/latex]from[latex]\textbf{B}[/latex]—that is, to finding[latex]\boldsymbol{\textbf{R}^{\prime\prime}=\textbf{B}-\textbf{A}=-\textbf{R}^{\prime}}[/latex]). Show that this is the case.

8: Show that the order of addition of three vectors does not affect their sum. Show this property by choosing any three vectors[latex]\textbf{A},\:\textbf{B},[/latex]and[latex]\textbf{C},[/latex]all having different lengths and directions. Find the sum[latex]\boldsymbol{\textbf{A}+\textbf{B}+\textbf{C}}[/latex]then find their sum when added in a different order and show the result is the same. (There are five other orders in which[latex]\textbf{A},\textbf{B},[/latex]and[latex]\textbf{C}[/latex]can be added; choose only one.)

9: Show that the sum of the vectors discussed in Example 2 gives the result shown in Figure 17 .

10: Find the magnitudes of velocities[latex]\boldsymbol{v_A}[/latex]and[latex]\boldsymbol{v_B}[/latex]in Figure 24

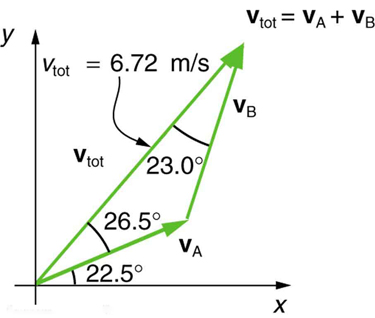
11: Find the components of[latex]\boldsymbol{v_{tot}}[/latex]along the x – and y -axes in Figure 24 .

12: Find the components of[latex]\boldsymbol{v_{tot}}[/latex]along a set of perpendicular axes rotated[latex]\boldsymbol{30^o}[/latex]counterclockwise relative to those in Figure 24 .

(a)[latex]\boldsymbol{480\textbf{ m}}[/latex]

(b)[latex]\boldsymbol{379\textbf{ m}},\boldsymbol{18.4^o}[/latex]east of north

north component 3.21 km, east component 3.83 km

[latex]\boldsymbol{19.5\textbf{ m}},\boldsymbol{4.65^o}[/latex]south of west

(a)[latex]\boldsymbol{26.6\textbf{ m}},\boldsymbol{65.1^o}[/latex]north of east

(b)[latex]\boldsymbol{26.6\textbf{ m}},\boldsymbol{65.1^o}[/latex]south of west

[latex]\boldsymbol{52.9\textbf{ m}},\boldsymbol{90.1^o}[/latex]with respect to the x -axis.

x -component 4.41 m/s

y -component 5.07 m/s

College Physics chapters 1-17 Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

This is a vector:

A vector has magnitude (size) and direction :

The length of the line shows its magnitude and the arrowhead points in the direction.

Play with one here:

We can add two vectors by joining them head-to-tail:

And it doesn't matter which order we add them, we get the same result:

Example: A plane is flying along, pointing North, but there is a wind coming from the North-West.

The two vectors (the velocity caused by the propeller, and the velocity of the wind) result in a slightly slower ground speed heading a little East of North.

If you watched the plane from the ground it would seem to be slipping sideways a little.

Have you ever seen that happen? Maybe you have seen birds struggling against a strong wind that seem to fly sideways. Vectors help explain that.

Velocity , acceleration , force and many other things are vectors.

Subtracting

We can also subtract one vector from another:

• first we reverse the direction of the vector we want to subtract,
• then add them as usual:

A vector is often written in bold , like a or b .

Calculations

Now ... how do we do the calculations?

The most common way is to first break up vectors into x and y parts, like this:

The vector a is broken up into the two vectors a x and a y

(We see later how to do this.)

Adding Vectors

We can then add vectors by adding the x parts and adding the y parts :

The vector (8, 13) and the vector (26, 7) add up to the vector (34, 20)

Example: add the vectors a = (8, 13) and b = (26, 7)

c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)

When we break up a vector like that, each part is called a component :

Subtracting Vectors

To subtract, first reverse the vector we want to subtract, then add.

Example: subtract k = (4, 5) from v = (12, 2)

a = v + − k

a = (12, 2) + −(4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)

Magnitude of a Vector

The magnitude of a vector is shown by two vertical bars on either side of the vector:

OR it can be written with double vertical bars (so as not to confuse it with absolute value):

We use Pythagoras' theorem to calculate it:

| a | = √( x 2 + y 2 )

Example: what is the magnitude of the vector b = (6, 8) ?

| b | = √( 6 2 + 8 2 ) = √(36+64) = √100 = 10

A vector with magnitude 1 is called a Unit Vector .

Vector vs Scalar

A scalar has magnitude (size) only .

Scalar: just a number (like 7 or −0.32) ... definitely not a vector.

A vector has magnitude and direction , and is often written in bold , so we know it is not a scalar:

• so c is a vector, it has magnitude and direction
• but c is just a value, like 3 or 12.4

Example: k b is actually the scalar k times the vector b .

Multiplying a vector by a scalar.

When we multiply a vector by a scalar it is called "scaling" a vector, because we change how big or small the vector is.

Example: multiply the vector m = (7, 3) by the scalar 3

It still points in the same direction, but is 3 times longer

(And now you know why numbers are called "scalars", because they "scale" the vector up or down.)

Multiplying a Vector by a Vector (Dot Product and Cross Product)

How do we multiply two vectors together? There is more than one way!

• The scalar or Dot Product (the result is a scalar).
• The vector or Cross Product (the result is a vector).

(Read those pages for more details.)

More Than 2 Dimensions

Vectors also work perfectly well in 3 or more dimensions:

Example: add the vectors a = (3, 7, 4) and b = (2, 9, 11)

c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)

Example: what is the magnitude of the vector w = (1, −2, 3) ?

| w | = √( 1 2 + (−2) 2 + 3 2 ) = √(1+4+9) = √14

Here is an example with 4 dimensions (but it is hard to draw!):

Example: subtract (1, 2, 3, 4) from (3, 3, 3, 3)

(3, 3, 3, 3) + −(1, 2, 3, 4) = (3, 3, 3, 3) + (−1,−2,−3,−4) = (3−1, 3−2, 3−3, 3−4) = (2, 1, 0, −1)

Magnitude and Direction

We may know a vector's magnitude and direction, but want its x and y lengths (or vice versa):

You can read how to convert them at Polar and Cartesian Coordinates , but here is a quick summary:

Sam and Alex are pulling a box.

• Sam pulls with 200 Newtons of force at 60°
• Alex pulls with 120 Newtons of force at 45° as shown

What is the combined force , and its direction?

Let us add the two vectors head to tail:

First convert from polar to Cartesian (to 2 decimals):

Sam's Vector:

• x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
• y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21

Alex's Vector:

• x = r × cos( θ ) = 120 × cos(−45°) = 120 × 0.7071 = 84.85
• y = r × sin( θ ) = 120 × sin(−45°) = 120 × -0.7071 = −84.85

Now we have:

(100,173.21) + (84.85, −84.85) = (184.85, 88.36)

That answer is valid, but let's convert back to polar as the question was in polar:

• r = √ ( x 2 + y 2 ) = √ ( 184.85 2 + 88.36 2 ) = 204.88
• θ = tan -1 ( y / x ) = tan -1 ( 88.36 / 184.85 ) = 25.5°

They might get a better result if they were shoulder-to-shoulder!

JEE-IIT-NCERT Physics & Math

Widget atas posting, vector addition and subtraction problems and solutions.

  Problem #1

Post a Comment for "Vector Addition And Subtraction Problems And Solutions"

Vector Addition and Subtraction

• Two people are pushing a disabled car. One exerts a force of 200 N east, the other a force of 150 N east. What is the net force exerted on the car? (Assume friction to be negligible.)
• Two soccer players kick a ball simultaneously from opposite sides. Red #3 kicks with 50 N of force while Blue #5 kicks with 63 N of force. What is the net force on the ball?
• An airplane heads due north at 100 m/s through a 30 m/s cross wind blowing from the east to the west. Determine the resultant velocity of the airplane (relative to due north).
• A mountain climbing expedition establishes a base camp and two intermediate camps, A and B. Camp A is 11,200 m east of and 3,200 m above base camp. Camp B is 8400 m east of and 1700 m higher than Camp A. Determine the displacement between base camp and Camp B.
• A plane heads east with a velocity of 52 m/s through a 12 m/s cross wind blowing the plane south. Find the magnitude and direction of the plane's resultant velocity (relative to due east).
• An ambitious hiker walks 25 km west and then 35 km south in a day. Find the magnitude and direction of the hiker's resultant displacement (relative to due west).
• A boat heads directly across a river with a velocity of 12 m/s. If the river flows at 6.0 m/s find the magnitude and direction of the boat's resultant velocity. (State the direction relative to an imaginary line drawn straight across the river.)
• What distance did I travel?
• What's my resultant displacement (magnitude and direction relative to due east)?
• the bearing that the plane should take (relative to due north)
• the plane's speed with respect to the air
• At a particular instant, a stationary observer on the ground sees a package falling from a moving airplane with a speed v observer at an angle θ to the vertical. To the pilot flying horizontally at a constant speed relative to the ground the package appears to be falling vertically with a speed v pilot at that same instant. What is the speed of the pilot relative to the ground in terms of the given quantities?

graphical drill

• worksheet-addition.pdf Determine the magnitude (in centimeters) and direction (in standard form) of the resultant vector B  +  A for each of the combinations below. Measure its length in centimeters and direction angle in standard form (i.e.; right 0°, up 90°, left 180°, down 270°, etc.). Use the horizontal reference lines as needed.
• worksheet-subtraction.pdf Determine the magnitude (in centimeters) and direction (in standard form) of the resultant vector B  −  A for each of the combinations below. Measure its length in centimeters and direction angle in standard form (i.e.; right 0°, up 90°, left 180°, down 270°, etc.). Use the horizontal reference lines as needed.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 4.10: Vector Addition and Subtraction: Analytical Methods

• Define the rules of vector addition and subtraction using analytical methods.
• Apply analytical methods to determine vertical and horizontal component vectors.
• Apply analytical methods to determine the magnitude and direction of a resultant vector.

Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.

You will be using trigonometry in this section.

Here is a very nice PHET simulation to help review those concepts.

https://phet.colorado.edu/en/simulation/trig-tour

Resolving a Vector into Perpendicular Components

Then A =10.3 blocks and θ =29.1° , so that

Calculating a Resultant Vector

DETERMINING VECTORS AND VECTOR COMPONENTS WITH ANALYTICAL METHODS

Adding Vectors Using Analytical Methods

Step 2. Find the components of the resultant along each axis by adding the components of the individual vectors along that axis . That is, as shown in Figure 7 ,

Step 3. To get the magnitude R of the resultant, use the Pythagorean theorem :

Step 4. To get the direction of the resultant:

The following example illustrates this technique for adding vectors using perpendicular components.

Example 1: Adding Vectors Using Analytical Methods

The x – and y -components of the resultant are thus

Now we can find the magnitude of the resultant by using the Pythagorean theorem:

Finally, we find the direction of the resultant:

This example illustrates the addition of vectors using perpendicular components. Vector subtraction using perpendicular components is very similar—it is just the addition of a negative vector.

and the rest of the method outlined above is identical to that for addition. (See Figure 10 .)

Analyzing vectors using perpendicular components is very useful in many areas of physics, because perpendicular quantities are often independent of one another.

PHET EXPLORATIONS: VECTOR ADDITION

Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.  Please note that this simulation uses Flash so it might not work on all machines.

• The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the magnitude and direction of a resultant vector.

Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the equations

Step 4: Use a trigonometric identity to determine the direction, θ , of R :

Conceptual Questions

2: Give an example of a nonzero vector that has a component of zero.

3: Explain why a vector cannot have a component greater than its own magnitude.

Problems & Exercises

1: Find the following for path C in Figure 12 : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.

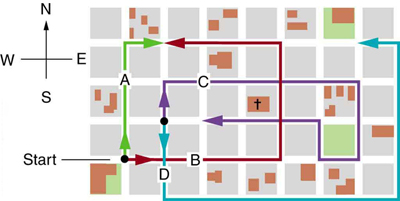
2: Find the following for path D in Figure 12 : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.

3: Find the north and east components of the displacement from San Francisco to Sacramento shown in Figure 13 .

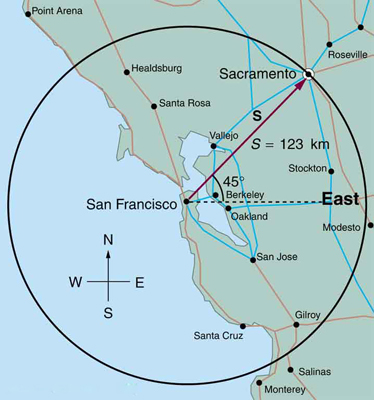
Note that you can also solve this graphically. Discuss why the analytical technique for solving this problem is potentially more accurate than the graphical technique.

6: You drive 7.50 km in a straight line in a direction 15° east of north. (a) Find the distances you would have to drive straight east and then straight north to arrive at the same point. (This determination is equivalent to find the components of the displacement along the east and north directions.) (b) Show that you still arrive at the same point if the east and north legs are reversed in order.

1: (a) 13 x 120 m = 1560 m = 1.56 km (b) 120 m  east

2: (a) 13 x 120 m = 1560 m = 1.56 km (b) magnitude = 646 m at 21.8   o North of East

3: North-component 87.0 km , east-component 87 km

4: 30.8 m , 35.8 degrees west of north

5: 30.8 m , 35.8 degrees west of north

Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 6.

• Vector word problem: resultant velocity
• Vector word problem: hiking
• Vector word problem: resultant force

Vector word problems

• Vectors: FAQ
• His first stop is 6  km ‍   to the east and 3  km ‍   to the south from his house.
• His second stop is 2  km ‍   to the west and 1  km ‍   to the south from the first stop.
• His third stop is 7  km ‍   to the west and 5  km ‍   to the north from the second stop.
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

• Scalars And Vectors
• Addition Of Vectors

Vector Addition and Subtraction

The vector addition is not as straightforward as the addition of scalars. Vectors have both magnitude and direction, and one cannot simply add two vectors to obtain their sum. To better understand this, let us consider an example of a car travelling 10 miles North and 10 miles South. Here, the total distance travelled is 20 miles, but the displacement is zero. The North and South displacements are each vector quantities, and the opposite directions cause the individual displacements to cancel each other out. In this article, let us explore ways to carry out vector addition and vector subtraction.

Vector Addition: Triangle, Parallelogram and Polygon Law of Vectors

As already discussed, vectors cannot be added algebraically. Following are a few points to remember while adding vectors:

• Vectors are added geometrically and not algebraically.
• Vectors whose resultant have to be calculated behave independently.
• Vector Addition is nothing but finding the resultant of a number of vectors acting on a body.
• Vector Addition is commutative. This means that the resultant vector is independent of the order of vectors. \(\begin{array}{l}\vec{A} + \vec{B} = \vec{B} + \vec{A}\end{array} \)

Triangle Law of Vector Addition

The vector addition is done based on the triangle law. Let us see what the triangle law of vector addition is:

Suppose there are two vectors, a and b.

Draw a line AB representing vector a with A as the tail and B as the head. Draw another line BC representing vector b with B as the tail and C as the head. Now join the line AC with A as the tail and C as the head. The line AC represents the resultant sum of the vectors a and b.

The line AC represents the resultant sum of the vectors a and b.

The magnitude of vectors a and b is:

a = magnitude of vector a

b = magnitude of vector b

θ = angle between vector a and b

Let the resultant make an angle of Φ with vector a, then:

Let us understand this using an example. Suppose two vectors have equal magnitude A, and they make an angle θ with each other. Now, to find the magnitude and direction of the resultant, we will use the formulas mentioned above.

Let the magnitude of the resultant vector be B.

Let’s say that the resultant vector makes an angle Ɵ with the first vector.

Read More: Triangle Law of Vector Addition

Parallelogram Law of Vector Addition

The vector addition may also be understood by the law of parallelogram. The law states, “If two vectors acting simultaneously at a point are represented in magnitude and direction by the two sides of a parallelogram drawn from a point, their resultant is given in magnitude and direction by the diagonal of the parallelogram passing through that point.”

According to this law, if two vectors, P and Q, are represented by two adjacent sides of a parallelogram pointing outwards, as shown in the figure below, then the diagonal drawn through the intersection of the two vectors represent the resultant.

In the Parallelogram Law of Vector Addition, the magnitude of the resultant is given by:

The direction of the resultant vector is determined as follows: \(\begin{array}{l}\tan\phi=\frac{CE}{AE}=\frac{Q\sin\theta}{P+Q\cos\theta}\end{array} \) \(\begin{array}{l}\theta=\tan^{-1}[\frac{Q\sin\theta}{P+Q\cos\theta}]\end{array} \)

Polygon Law of Vector

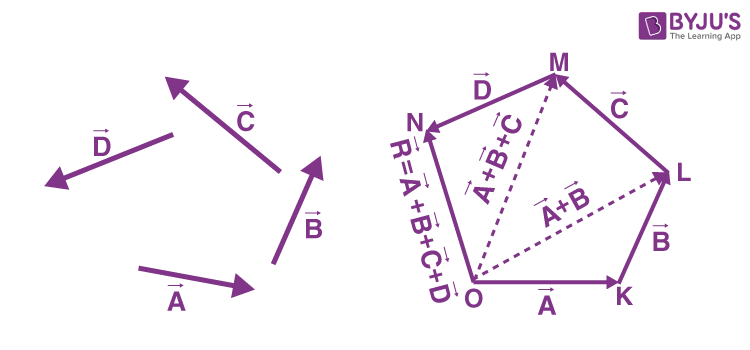
From the triangle law of vector addition, we know that triangle OLM can be expressed as vector OM is the resultant of the vectors OL and LM.

Again, applying the triangle law of vector addition to triangle OMN,

From eq.2, we get,

Considering vector ON=vector R, the equation becomes

Click the below video to understand the application of the polygon law of vector addition

Properties of Vector Addition

The vector addition is the sum of multiple (two or more) vectors. Two laws related to the addition of vectors are parallelogram law and triangle law. Similarly, the properties related to vector addition are:

• Associative Property
• Commutative Property

Vector Subtraction

The subtraction of two vectors is similar to addition. Suppose vector a is to be subtracted from vector b.

vector a – vector b can be said as the addition of vectors a and -b. Thus, the addition formula can be applied as:

vector (-b) is nothing but vector b reversed in direction.

Related articles:

Frequently Asked Questions – FAQs

What is the maximum and minimum sum of two vectors.

The maximum sum of two vectors is obtained when the two vectors are directed in the same direction. The minimum sum is obtained when the two vectors are directed in the opposite direction.

Is vector addition commutative?

Yes, vector addition is commutative.

Is vector addition applicable to any two vectors?

No, vector addition does not apply to any two vectors. Two vectors are added only when they are of the same type and nature. For instance, two velocity vectors can be added, but one velocity vector and one force vector cannot be added.

State the associative property of vector addition.

The associative property of vector addition states that the sum of the vectors remains the same regardless of the order in which they are arranged.

Can the sum of two vectors have a zero?

Yes, two vectors with equal magnitude and pointing in opposite directions will have the sum equal to zero.

Watch the video and learn about the analytical method of Vector Addition

Stay tuned with BYJU’S to learn more about vectors, vector notation and much more.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Well explained

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

12 3.3 Vector Addition and Subtraction: Analytical Methods

• Understand the rules of vector addition and subtraction using analytical methods.
• Apply analytical methods to determine vertical and horizontal component vectors.
• Apply analytical methods to determine the magnitude and direction of a resultant vector.

Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.

Resolving a Vector into Perpendicular Components

Calculating a Resultant Vector

DETERMINING VECTORS AND VECTOR COMPONENTS WITH ANALYTICAL METHODS

Adding Vectors Using Analytical Methods

Step 2. Find the components of the resultant along each axis by adding the components of the individual vectors along that axis . That is, as shown in Figure 7 ,

Step 4. To get the direction of the resultant:

The following example illustrates this technique for adding vectors using perpendicular components.

Example 1: Adding Vectors Using Analytical Methods

The x – and y -components of the resultant are thus

Now we can find the magnitude of the resultant by using the Pythagorean theorem:

Finally, we find the direction of the resultant:

This example illustrates the addition of vectors using perpendicular components. Vector subtraction using perpendicular components is very similar—it is just the addition of a negative vector.

and the rest of the method outlined above is identical to that for addition. (See Figure 10 .)

Analyzing vectors using perpendicular components is very useful in many areas of physics, because perpendicular quantities are often independent of one another. The next module, Chapter 3.4 Projectile Motion , is one of many in which using perpendicular components helps make the picture clear and simplifies the physics.

PHET EXPLORATIONS: VECTOR ADDITION

Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.

• The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the magnitude and direction of a resultant vector.

Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the equations

Conceptual Questions

2: Give an example of a nonzero vector that has a component of zero.

3: Explain why a vector cannot have a component greater than its own magnitude.

Problems & Exercises

1: Find the following for path C in Figure 12 : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.

2: Find the following for path D in Figure 12 : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.

3: Find the north and east components of the displacement from San Francisco to Sacramento shown in Figure 13 .

Note that you can also solve this graphically. Discuss why the analytical technique for solving this problem is potentially more accurate than the graphical technique.

(a) 1.56 km

(b) 120 m east

North-component 87.0 km, east-component 87.0 km

30.8 m, 35.8 west of north

(a) 18.4 km south, then 26.2 km west

3.3 Vector Addition and Subtraction: Analytical Methods by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8 Vector Addition and Subtraction: Analytical Methods

[latexpage]

Learning Objectives

• Understand the rules of vector addition and subtraction using analytical methods.
• Apply analytical methods to determine vertical and horizontal component vectors.
• Apply analytical methods to determine the magnitude and direction of a resultant vector.

Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.

Resolving a Vector into Perpendicular Components

Analytical techniques and right triangles go hand-in-hand in physics because (among other things) motions along perpendicular directions are independent. We very often need to separate a vector into perpendicular components. For example, given a vector like \(\mathbf{A}\) in (Figure) , we may wish to find which two perpendicular vectors, \({\mathbf{A}}_{x}\) and \({\mathbf{A}}_{y}\), add to produce it.

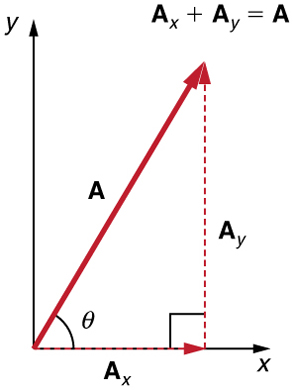
\({\mathbf{A}}_{x}\) and \({\mathbf{A}}_{y}\) are defined to be the components of \(\mathbf{A}\) along the x – and y -axes. The three vectors \(\mathbf{A}\), \({\mathbf{A}}_{x}\), and \({\mathbf{A}}_{y}\) form a right triangle:

Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). The relationship does not apply for the magnitudes alone. For example, if \({\mathbf{\text{A}}}_{x}=3 m\) east, \({\mathbf{\text{A}}}_{y}=4 m\) north, and \(\mathbf{\text{A}}=5 m\) north-east, then it is true that the vectors \({\mathbf{A}}_{x}{\text{ + A}}_{y}\text{ = A}\). However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,

If the vector \(\mathbf{A}\) is known, then its magnitude \(A\) (its length) and its angle \(\theta \) (its direction) are known. To find \({A}_{x}\) and \({A}_{y}\), its x – and y -components, we use the following relationships for a right triangle.

Suppose, for example, that \(\mathbf{A}\) is the vector representing the total displacement of the person walking in a city considered in Kinematics in Two Dimensions: An Introduction and Vector Addition and Subtraction: Graphical Methods .

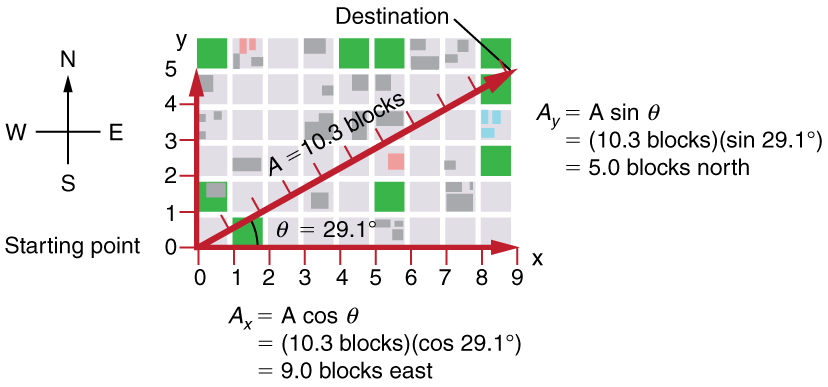
Then \(A=10.3\) blocks and \(\theta =29.1º\) , so that

Calculating a Resultant Vector

If the perpendicular components \({\mathbf{A}}_{x}\) and \({\mathbf{A}}_{y}\) of a vector \(\mathbf{A}\) are known, then \(\mathbf{A}\) can also be found analytically. To find the magnitude \(A\) and direction \(\theta \) of a vector from its perpendicular components \({\mathbf{A}}_{x}\) and \({\mathbf{A}}_{y}\), we use the following relationships:

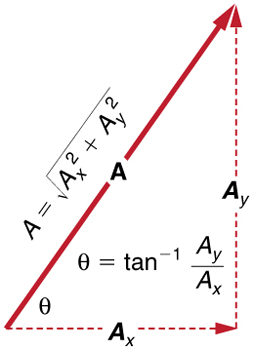
Note that the equation \(A=\sqrt{{A}_{x}^{2}+{A}_{y}^{2}}\) is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if \({A}_{x}\) and \({A}_{y}\) are 9 and 5 blocks, respectively, then \(A=\sqrt{{9}^{2}{\text{+5}}^{2}}\text{=10}\text{.}3\) blocks, again consistent with the example of the person walking in a city. Finally, the direction is \(\theta ={\text{tan}}^{–1}\left(\text{5/9}\right)=29.1º\) , as before.

Equations \({A}_{x}=A\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \) and \({A}_{y}=A\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta \) are used to find the perpendicular components of a vector—that is, to go from \(A\) and \(\theta \) to \({A}_{x}\) and \({A}_{y}\). Equations \(A=\sqrt{{A}_{x}^{2}+{A}_{y}^{2}}\) and \(\theta ={\text{tan}}^{\text{–1}}\left({A}_{y}/{A}_{x}\right)\) are used to find a vector from its perpendicular components—that is, to go from \({A}_{x}\) and \({A}_{y}\) to \(A\) and \(\theta \). Both processes are crucial to analytical methods of vector addition and subtraction.

Adding Vectors Using Analytical Methods

To see how to add vectors using perpendicular components, consider (Figure) , in which the vectors \(\mathbf{A}\) and \(\mathbf{B}\) are added to produce the resultant \(\mathbf{R}\).

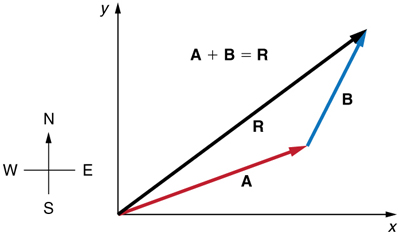
If \(\mathbf{A}\) and \(\mathbf{B}\) represent two legs of a walk (two displacements), then \(\mathbf{R}\) is the total displacement. The person taking the walk ends up at the tip of \(\mathbf{R}.\) There are many ways to arrive at the same point. In particular, the person could have walked first in the x -direction and then in the y -direction. Those paths are the x – and y -components of the resultant, \({\mathbf{R}}_{x}\) and \({\mathbf{R}}_{y}\). If we know \({\mathbf{\text{R}}}_{x}\) and \({\mathbf{R}}_{y}\), we can find \(R\) and \(\theta \) using the equations \(A=\sqrt{{{A}_{x}}^{2}+{{A}_{y}}^{2}}\) and \(\theta ={\text{tan}}^{–1}\left({A}_{y}/{A}_{x}\right)\). When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.

Step 1. Identify the x- and y-axes that will be used in the problem. Then, find the components of each vector to be added along the chosen perpendicular axes . Use the equations \({A}_{x}=A\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \) and \({A}_{y}=A\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta \) to find the components. In (Figure) , these components are \({A}_{x}\), \({A}_{y}\), \({B}_{x}\), and \({B}_{y}\). The angles that vectors \(\mathbf{A}\) and \(\mathbf{B}\) make with the x -axis are \({\theta }_{\text{A}}\) and \({\theta }_{\text{B}}\), respectively.

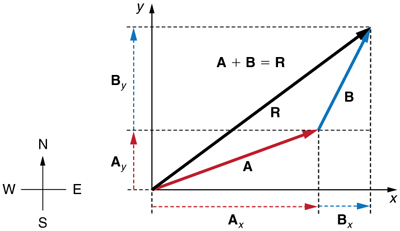
Step 2. Find the components of the resultant along each axis by adding the components of the individual vectors along that axis . That is, as shown in (Figure) ,

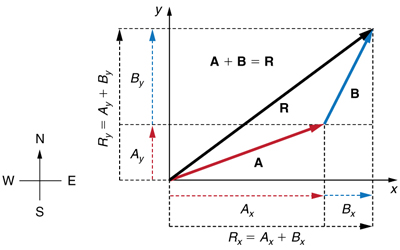
Components along the same axis, say the x -axis, are vectors along the same line and, thus, can be added to one another like ordinary numbers. The same is true for components along the y -axis. (For example, a 9-block eastward walk could be taken in two legs, the first 3 blocks east and the second 6 blocks east, for a total of 9, because they are along the same direction.) So resolving vectors into components along common axes makes it easier to add them. Now that the components of \(\mathbf{R}\) are known, its magnitude and direction can be found.

Step 3. To get the magnitude \(R\) of the resultant, use the Pythagorean theorem:

Step 4. To get the direction of the resultant:

The following example illustrates this technique for adding vectors using perpendicular components.

Add the vector \(\mathbf{A}\) to the vector \(\mathbf{B}\) shown in (Figure) , using perpendicular components along the x – and y -axes. The x – and y -axes are along the east–west and north–south directions, respectively. Vector \(\mathbf{A}\) represents the first leg of a walk in which a person walks \(\text{53}\text{.}\text{0 m}\) in a direction \(\text{20}\text{.}0\text{º}\) north of east. Vector \(\mathbf{B}\) represents the second leg, a displacement of \(\text{34}\text{.}\text{0 m}\) in a direction \(\text{63}\text{.}0\text{º}\) north of east.

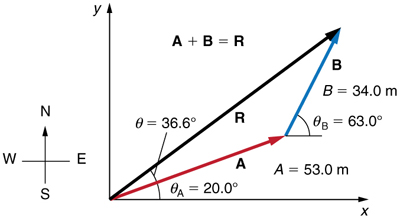
The components of \(\mathbf{A}\) and \(\mathbf{B}\) along the x – and y -axes represent walking due east and due north to get to the same ending point. Once found, they are combined to produce the resultant.

Following the method outlined above, we first find the components of \(\mathbf{A}\) and \(\mathbf{B}\) along the x – and y -axes. Note that \(A=53.0 m\text{}\), \({\theta }_{\text{A}}=20.0º\), \(B=34.0 m\text{}\), and \({\theta }_{\text{B}}=63.0º\). We find the x -components by using \({A}_{x}=A\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \), which gives

Similarly, the y -components are found using \({A}_{y}=A\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{A}\):

The x – and y -components of the resultant are thus

Now we can find the magnitude of the resultant by using the Pythagorean theorem:

Finally, we find the direction of the resultant:

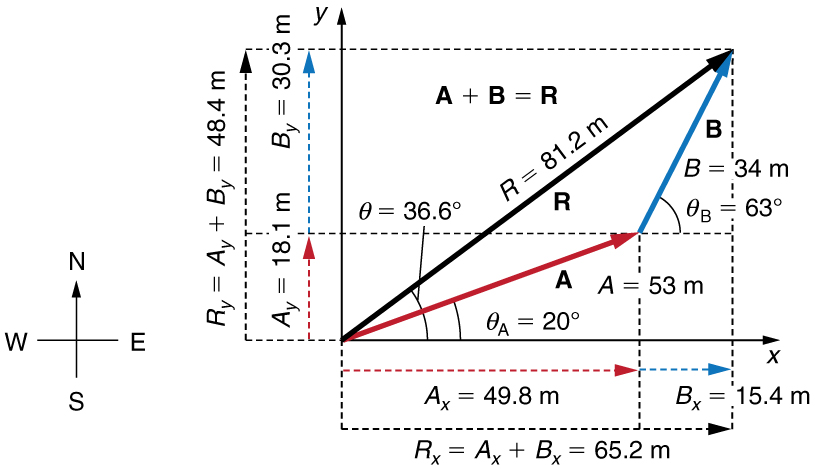
This example illustrates the addition of vectors using perpendicular components. Vector subtraction using perpendicular components is very similar—it is just the addition of a negative vector.

Subtraction of vectors is accomplished by the addition of a negative vector. That is, \(\mathbf{A}-\mathbf{B}\equiv \mathbf{A}+\left(\mathbf{–B}\right)\). Thus, the method for the subtraction of vectors using perpendicular components is identical to that for addition . The components of \(\mathbf{\text{–B}}\) are the negatives of the components of \(\mathbf{B}\). The x – and y -components of the resultant \(\mathbf{A}-\text{B = R}\) are thus

and the rest of the method outlined above is identical to that for addition. (See (Figure) .)

Analyzing vectors using perpendicular components is very useful in many areas of physics, because perpendicular quantities are often independent of one another. The next module, Projectile Motion , is one of many in which using perpendicular components helps make the picture clear and simplifies the physics.

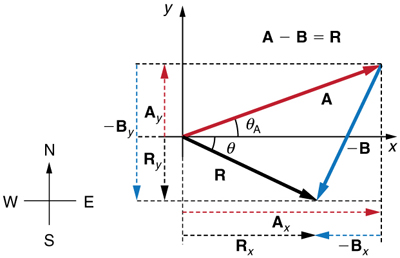
Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.

• The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the magnitude and direction of a resultant vector.

Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the equations

Step 2: Add the horizontal and vertical components of each vector to determine the components \({R}_{x}\) and \({R}_{y}\) of the resultant vector, \(\mathbf{\text{R}}\):

Step 3: Use the Pythagorean theorem to determine the magnitude, \(R\), of the resultant vector \(\mathbf{\text{R}}\):

Step 4: Use a trigonometric identity to determine the direction, \(\theta \), of \(\mathbf{\text{R}}\):

Conceptual Questions

Suppose you add two vectors \(\mathbf{A}\) and \(\mathbf{B}\). What relative direction between them produces the resultant with the greatest magnitude? What is the maximum magnitude? What relative direction between them produces the resultant with the smallest magnitude? What is the minimum magnitude?

Give an example of a nonzero vector that has a component of zero.

Explain why a vector cannot have a component greater than its own magnitude.

If the vectors \(\mathbf{A}\) and \(\mathbf{B}\) are perpendicular, what is the component of \(\mathbf{A}\) along the direction of \(\mathbf{B}\)? What is the component of \(\mathbf{B}\) along the direction of \(\mathbf{A}\)?

Problems & Exercises

Find the following for path C in (Figure) : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.

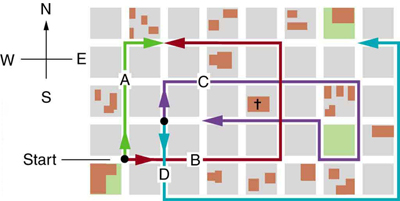
(a) 1.56 km

(b) 120 m east

Find the following for path D in (Figure) : (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.

Find the north and east components of the displacement from San Francisco to Sacramento shown in (Figure) .

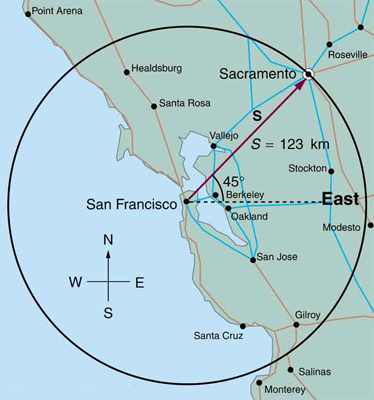
North-component 87.0 km, east-component 87.0 km

Solve the following problem using analytical techniques: Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements \(\mathbf{A}\) and \(\mathbf{B}\), as in (Figure) , then this problem asks you to find their sum \(\mathbf{R}=\mathbf{A}+\mathbf{B}\).)

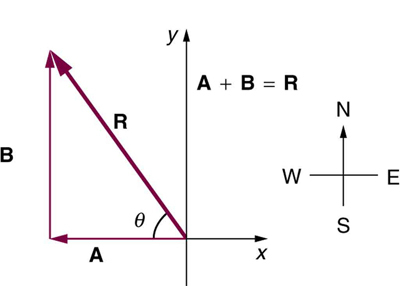
Note that you can also solve this graphically. Discuss why the analytical technique for solving this problem is potentially more accurate than the graphical technique.

Repeat (Figure) using analytical techniques, but reverse the order of the two legs of the walk and show that you get the same final result. (This problem shows that adding them in reverse order gives the same result—that is, \(\mathbf{\text{B + A = A + B}}\).) Discuss how taking another path to reach the same point might help to overcome an obstacle blocking you other path.

30.8 m, 35.8 west of north

You drive \(7\text{.}\text{50 km}\) in a straight line in a direction \(15º\) east of north. (a) Find the distances you would have to drive straight east and then straight north to arrive at the same point. (This determination is equivalent to find the components of the displacement along the east and north directions.) (b) Show that you still arrive at the same point if the east and north legs are reversed in order.

Do (Figure) again using analytical techniques and change the second leg of the walk to \(\text{25.0 m}\) straight south. (This is equivalent to subtracting \(\mathbf{B}\) from \(\mathbf{A}\) —that is, finding \(\mathbf{\text{R}}\prime =\mathbf{\text{A – B}}\)) (b) Repeat again, but now you first walk \(\text{25}\text{.}\text{0 m}\) north and then \(\text{18}\text{.}\text{0 m}\) east. (This is equivalent to subtract \(\mathbf{A}\) from \(\mathbf{B}\) —that is, to find \(\mathbf{A}=\mathbf{B}+\mathbf{C}\). Is that consistent with your result?)

(a) \(\text{30}\text{.}\text{8 m}\), \(\text{54}\text{.}2º\) south of west

(b) \(\text{30}\text{.}\text{8 m}\), \(\text{54}\text{.}2º\) north of east

A new landowner has a triangular piece of flat land she wishes to fence. Starting at the west corner, she measures the first side to be 80.0 m long and the next to be 105 m. These sides are represented as displacement vectors \(\mathbf{A}\) from \(\mathbf{B}\) in (Figure) . She then correctly calculates the length and orientation of the third side \(\text{C}\). What is her result?

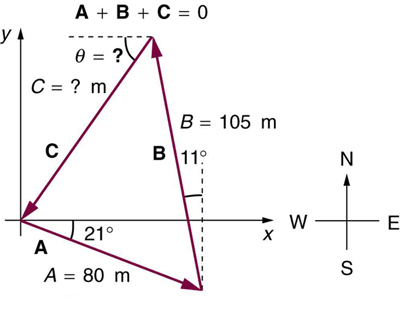
You fly \(\text{32}\text{.}\text{0 km}\) in a straight line in still air in the direction \(35.0º\) south of west. (a) Find the distances you would have to fly straight south and then straight west to arrive at the same point. (This determination is equivalent to finding the components of the displacement along the south and west directions.) (b) Find the distances you would have to fly first in a direction \(45.0º\) south of west and then in a direction \(45.0º\) west of north. These are the components of the displacement along a different set of axes—one rotated \(45º\).

18.4 km south, then 26.2 km west(b) 31.5 km at \(45.0º\) south of west, then 5.56 km at \(45.0º\) west of north

A farmer wants to fence off his four-sided plot of flat land. He measures the first three sides, shown as \(\mathbf{A},\) \(\mathbf{B},\) and \(\mathbf{C}\) in (Figure) , and then correctly calculates the length and orientation of the fourth side \(\mathbf{D}\). What is his result?

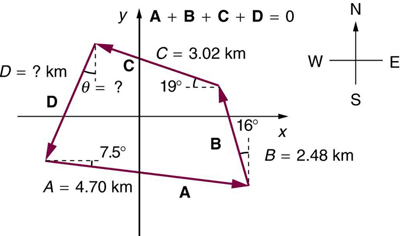
In an attempt to escape his island, Gilligan builds a raft and sets to sea. The wind shifts a great deal during the day, and he is blown along the following straight lines: \(2\text{.}\text{50 km}\) \(45.0º\) north of west; then \(4\text{.}\text{70 km}\) \(60.0º\) south of east; then \(1.30\phantom{\rule{0.25em}{0ex}}\text{km}\) \(25.0º\) south of west; then \(5\text{.}\text{10 km}\) straight east; then \(1.70\phantom{\rule{0.25em}{0ex}}\text{km}\) \(5.00º\) east of north; then \(7\text{.}\text{20 km}\) \(55.0º\) south of west; and finally \(2\text{.}\text{80 km}\) \(10.0º\) north of east. What is his final position relative to the island?

\(7\text{.}\text{34 km}\), \(\text{63}\text{.}5º\) south of east

Suppose a pilot flies \(\text{40}\text{.}\text{0 km}\) in a direction \(\text{60º}\) north of east and then flies \(\text{30}\text{.}\text{0 km}\) in a direction \(\text{15º}\) north of east as shown in (Figure) . Find her total distance \(R\) from the starting point and the direction \(\theta \) of the straight-line path to the final position. Discuss qualitatively how this flight would be altered by a wind from the north and how the effect of the wind would depend on both wind speed and the speed of the plane relative to the air mass.

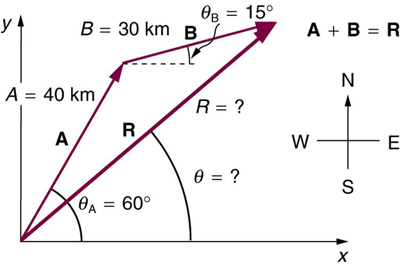
Intro to Physics for Non-Majors Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book