null hypothesis for chi squared test

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Chi-Square (Χ²) Tests | Types, Formula & Examples

Chi-Square (Χ²) Tests | Types, Formula & Examples

Published on May 23, 2022 by Shaun Turney . Revised on June 22, 2023.

A Pearson’s chi-square test is a statistical test for categorical data. It is used to determine whether your data are significantly different from what you expected. There are two types of Pearson’s chi-square tests:

• The chi-square goodness of fit test is used to test whether the frequency distribution of a categorical variable is different from your expectations.
• The chi-square test of independence is used to test whether two categorical variables are related to each other.

Table of contents

What is a chi-square test, the chi-square formula, when to use a chi-square test, types of chi-square tests, how to perform a chi-square test, how to report a chi-square test, practice questions, other interesting articles, frequently asked questions about chi-square tests.

Pearson’s chi-square (Χ 2 ) tests, often referred to simply as chi-square tests, are among the most common nonparametric tests . Nonparametric tests are used for data that don’t follow the assumptions of parametric tests , especially the assumption of a normal distribution .

If you want to test a hypothesis about the distribution of a categorical variable you’ll need to use a chi-square test or another nonparametric test. Categorical variables can be nominal or ordinal and represent groupings such as species or nationalities. Because they can only have a few specific values, they can’t have a normal distribution.

Test hypotheses about frequency distributions

There are two types of Pearson’s chi-square tests, but they both test whether the observed frequency distribution of a categorical variable is significantly different from its expected frequency distribution. A frequency distribution describes how observations are distributed between different groups.

Frequency distributions are often displayed using frequency distribution tables . A frequency distribution table shows the number of observations in each group. When there are two categorical variables, you can use a specific type of frequency distribution table called a contingency table to show the number of observations in each combination of groups.

Prevent plagiarism. Run a free check.

Both of Pearson’s chi-square tests use the same formula to calculate the test statistic , chi-square (Χ 2 ):

• Χ 2 is the chi-square test statistic
• Σ is the summation operator (it means “take the sum of”)
• O is the observed frequency
• E is the expected frequency

The larger the difference between the observations and the expectations ( O − E in the equation), the bigger the chi-square will be. To decide whether the difference is big enough to be statistically significant , you compare the chi-square value to a critical value.

A Pearson’s chi-square test may be an appropriate option for your data if all of the following are true:

• You want to test a hypothesis about one or more categorical variables . If one or more of your variables is quantitative, you should use a different statistical test . Alternatively, you could convert the quantitative variable into a categorical variable by separating the observations into intervals.
• The sample was randomly selected from the population .
• There are a minimum of five observations expected in each group or combination of groups.

The two types of Pearson’s chi-square tests are:

Chi-square goodness of fit test

Chi-square test of independence.

Mathematically, these are actually the same test. However, we often think of them as different tests because they’re used for different purposes.

You can use a chi-square goodness of fit test when you have one categorical variable. It allows you to test whether the frequency distribution of the categorical variable is significantly different from your expectations. Often, but not always, the expectation is that the categories will have equal proportions.

• Null hypothesis ( H 0 ): The bird species visit the bird feeder in equal proportions.
• Alternative hypothesis ( H A ): The bird species visit the bird feeder in different proportions.

Expectation of different proportions

• Null hypothesis ( H 0 ): The bird species visit the bird feeder in the same proportions as the average over the past five years.
• Alternative hypothesis ( H A ): The bird species visit the bird feeder in different proportions from the average over the past five years.

You can use a chi-square test of independence when you have two categorical variables. It allows you to test whether the two variables are related to each other. If two variables are independent (unrelated), the probability of belonging to a certain group of one variable isn’t affected by the other variable .

• Null hypothesis ( H 0 ): The proportion of people who are left-handed is the same for Americans and Canadians.
• Alternative hypothesis ( H A ): The proportion of people who are left-handed differs between nationalities.

Other types of chi-square tests

Some consider the chi-square test of homogeneity to be another variety of Pearson’s chi-square test. It tests whether two populations come from the same distribution by determining whether the two populations have the same proportions as each other. You can consider it simply a different way of thinking about the chi-square test of independence.

McNemar’s test is a test that uses the chi-square test statistic. It isn’t a variety of Pearson’s chi-square test, but it’s closely related. You can conduct this test when you have a related pair of categorical variables that each have two groups. It allows you to determine whether the proportions of the variables are equal.

• Null hypothesis ( H 0 ): The proportion of people who like chocolate is the same as the proportion of people who like vanilla.
• Alternative hypothesis ( H A ): The proportion of people who like chocolate is different from the proportion of people who like vanilla.

There are several other types of chi-square tests that are not Pearson’s chi-square tests, including the test of a single variance and the likelihood ratio chi-square test .

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

The exact procedure for performing a Pearson’s chi-square test depends on which test you’re using, but it generally follows these steps:

• Create a table of the observed and expected frequencies. This can sometimes be the most difficult step because you will need to carefully consider which expected values are most appropriate for your null hypothesis.
• Calculate the chi-square value from your observed and expected frequencies using the chi-square formula.
• Find the critical chi-square value in a chi-square critical value table or using statistical software.
• Compare the chi-square value to the critical value to determine which is larger.
• Decide whether to reject the null hypothesis. You should reject the null hypothesis if the chi-square value is greater than the critical value. If you reject the null hypothesis, you can conclude that your data are significantly different from what you expected.

If you decide to include a Pearson’s chi-square test in your research paper , dissertation or thesis , you should report it in your results section . You can follow these rules if you want to report statistics in APA Style :

• You don’t need to provide a reference or formula since the chi-square test is a commonly used statistic.
• Refer to chi-square using its Greek symbol, Χ 2 . Although the symbol looks very similar to an “X” from the Latin alphabet, it’s actually a different symbol. Greek symbols should not be italicized.
• Include a space on either side of the equal sign.
• If your chi-square is less than zero, you should include a leading zero (a zero before the decimal point) since the chi-square can be greater than zero.
• Provide two significant digits after the decimal point.
• Report the chi-square alongside its degrees of freedom , sample size, and p value , following this format: Χ 2 (degrees of freedom, N = sample size) = chi-square value, p = p value).

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Chi square test of independence
• Statistical power
• Descriptive statistics
• Degrees of freedom
• Pearson correlation
• Null hypothesis

Methodology

• Double-blind study
• Case-control study
• Research ethics
• Data collection
• Hypothesis testing
• Structured interviews

Research bias

• Hawthorne effect
• Unconscious bias
• Recall bias
• Halo effect
• Self-serving bias
• Information bias

The two main chi-square tests are the chi-square goodness of fit test and the chi-square test of independence .

Both chi-square tests and t tests can test for differences between two groups. However, a t test is used when you have a dependent quantitative variable and an independent categorical variable (with two groups). A chi-square test of independence is used when you have two categorical variables.

Both correlations and chi-square tests can test for relationships between two variables. However, a correlation is used when you have two quantitative variables and a chi-square test of independence is used when you have two categorical variables.

Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).

Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).

You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). Chi-Square (Χ²) Tests | Types, Formula & Examples. Scribbr. Retrieved April 17, 2024, from https://www.scribbr.com/statistics/chi-square-tests/

Is this article helpful?

Shaun Turney

Other students also liked, chi-square test of independence | formula, guide & examples, chi-square goodness of fit test | formula, guide & examples, chi-square (χ²) distributions | definition & examples, what is your plagiarism score.

Hypothesis Testing - Chi Squared Test

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific tests considered here are called chi-square tests and are appropriate when the outcome is discrete (dichotomous, ordinal or categorical). For example, in some clinical trials the outcome is a classification such as hypertensive, pre-hypertensive or normotensive. We could use the same classification in an observational study such as the Framingham Heart Study to compare men and women in terms of their blood pressure status - again using the classification of hypertensive, pre-hypertensive or normotensive status.  

The technique to analyze a discrete outcome uses what is called a chi-square test. Specifically, the test statistic follows a chi-square probability distribution. We will consider chi-square tests here with one, two and more than two independent comparison groups.

Learning Objectives

After completing this module, the student will be able to:

• Perform chi-square tests by hand
• Appropriately interpret results of chi-square tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

Tests with One Sample, Discrete Outcome

Here we consider hypothesis testing with a discrete outcome variable in a single population. Discrete variables are variables that take on more than two distinct responses or categories and the responses can be ordered or unordered (i.e., the outcome can be ordinal or categorical). The procedure we describe here can be used for dichotomous (exactly 2 response options), ordinal or categorical discrete outcomes and the objective is to compare the distribution of responses, or the proportions of participants in each response category, to a known distribution. The known distribution is derived from another study or report and it is again important in setting up the hypotheses that the comparator distribution specified in the null hypothesis is a fair comparison. The comparator is sometimes called an external or a historical control.   

In one sample tests for a discrete outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the proportions of participants in each response

Test Statistic for Testing H 0 : p 1 = p 10 , p 2 = p 20 , ..., p k = p k0

We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1. In the test statistic, O = observed frequency and E=expected frequency in each of the response categories. The observed frequencies are those observed in the sample and the expected frequencies are computed as described below. χ 2 (chi-square) is another probability distribution and ranges from 0 to ∞. The test above statistic formula above is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories.  

When we conduct a χ 2 test, we compare the observed frequencies in each response category to the frequencies we would expect if the null hypothesis were true. These expected frequencies are determined by allocating the sample to the response categories according to the distribution specified in H 0 . This is done by multiplying the observed sample size (n) by the proportions specified in the null hypothesis (p 10 , p 20 , ..., p k0 ). To ensure that the sample size is appropriate for the use of the test statistic above, we need to ensure that the following: min(np 10 , n p 20 , ..., n p k0 ) > 5.  

The test of hypothesis with a discrete outcome measured in a single sample, where the goal is to assess whether the distribution of responses follows a known distribution, is called the χ 2 goodness-of-fit test. As the name indicates, the idea is to assess whether the pattern or distribution of responses in the sample "fits" a specified population (external or historical) distribution. In the next example we illustrate the test. As we work through the example, we provide additional details related to the use of this new test statistic.  

A University conducted a survey of its recent graduates to collect demographic and health information for future planning purposes as well as to assess students' satisfaction with their undergraduate experiences. The survey revealed that a substantial proportion of students were not engaging in regular exercise, many felt their nutrition was poor and a substantial number were smoking. In response to a question on regular exercise, 60% of all graduates reported getting no regular exercise, 25% reported exercising sporadically and 15% reported exercising regularly as undergraduates. The next year the University launched a health promotion campaign on campus in an attempt to increase health behaviors among undergraduates. The program included modules on exercise, nutrition and smoking cessation. To evaluate the impact of the program, the University again surveyed graduates and asked the same questions. The survey was completed by 470 graduates and the following data were collected on the exercise question:

Based on the data, is there evidence of a shift in the distribution of responses to the exercise question following the implementation of the health promotion campaign on campus? Run the test at a 5% level of significance.

In this example, we have one sample and a discrete (ordinal) outcome variable (with three response options). We specifically want to compare the distribution of responses in the sample to the distribution reported the previous year (i.e., 60%, 25%, 15% reporting no, sporadic and regular exercise, respectively). We now run the test using the five-step approach.  

• Step 1. Set up hypotheses and determine level of significance.

The null hypothesis again represents the "no change" or "no difference" situation. If the health promotion campaign has no impact then we expect the distribution of responses to the exercise question to be the same as that measured prior to the implementation of the program.

H 0 : p 1 =0.60, p 2 =0.25, p 3 =0.15,  or equivalently H 0 : Distribution of responses is 0.60, 0.25, 0.15  

H 1 :   H 0 is false.          α =0.05

Notice that the research hypothesis is written in words rather than in symbols. The research hypothesis as stated captures any difference in the distribution of responses from that specified in the null hypothesis. We do not specify a specific alternative distribution, instead we are testing whether the sample data "fit" the distribution in H 0 or not. With the χ 2 goodness-of-fit test there is no upper or lower tailed version of the test.

• Step 2. Select the appropriate test statistic.  

The test statistic is:

We must first assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=470 and the proportions specified in the null hypothesis are 0.60, 0.25 and 0.15. Thus, min( 470(0.65), 470(0.25), 470(0.15))=min(282, 117.5, 70.5)=70.5. The sample size is more than adequate so the formula can be used.

• Step 3. Set up decision rule.  

The decision rule for the χ 2 test depends on the level of significance and the degrees of freedom, defined as degrees of freedom (df) = k-1 (where k is the number of response categories). If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. Critical values can be found in a table of probabilities for the χ 2 distribution. Here we have df=k-1=3-1=2 and a 5% level of significance. The appropriate critical value is 5.99, and the decision rule is as follows: Reject H 0 if χ 2 > 5.99.

• Step 4. Compute the test statistic.  

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) and the expected frequencies into the formula for the test statistic identified in Step 2. The computations can be organized as follows.

Notice that the expected frequencies are taken to one decimal place and that the sum of the observed frequencies is equal to the sum of the expected frequencies. The test statistic is computed as follows:

• Step 5. Conclusion.  

We reject H 0 because 8.46 > 5.99. We have statistically significant evidence at α=0.05 to show that H 0 is false, or that the distribution of responses is not 0.60, 0.25, 0.15.  The p-value is p < 0.005.  

In the χ 2 goodness-of-fit test, we conclude that either the distribution specified in H 0 is false (when we reject H 0 ) or that we do not have sufficient evidence to show that the distribution specified in H 0 is false (when we fail to reject H 0 ). Here, we reject H 0 and concluded that the distribution of responses to the exercise question following the implementation of the health promotion campaign was not the same as the distribution prior. The test itself does not provide details of how the distribution has shifted. A comparison of the observed and expected frequencies will provide some insight into the shift (when the null hypothesis is rejected). Does it appear that the health promotion campaign was effective?  

Consider the following: 

If the null hypothesis were true (i.e., no change from the prior year) we would have expected more students to fall in the "No Regular Exercise" category and fewer in the "Regular Exercise" categories. In the sample, 255/470 = 54% reported no regular exercise and 90/470=19% reported regular exercise. Thus, there is a shift toward more regular exercise following the implementation of the health promotion campaign. There is evidence of a statistical difference, is this a meaningful difference? Is there room for improvement?

The National Center for Health Statistics (NCHS) provided data on the distribution of weight (in categories) among Americans in 2002. The distribution was based on specific values of body mass index (BMI) computed as weight in kilograms over height in meters squared. Underweight was defined as BMI< 18.5, Normal weight as BMI between 18.5 and 24.9, overweight as BMI between 25 and 29.9 and obese as BMI of 30 or greater. Americans in 2002 were distributed as follows: 2% Underweight, 39% Normal Weight, 36% Overweight, and 23% Obese. Suppose we want to assess whether the distribution of BMI is different in the Framingham Offspring sample. Using data from the n=3,326 participants who attended the seventh examination of the Offspring in the Framingham Heart Study we created the BMI categories as defined and observed the following:

• Step 1.  Set up hypotheses and determine level of significance.

H 0 : p 1 =0.02, p 2 =0.39, p 3 =0.36, p 4 =0.23     or equivalently

H 0 : Distribution of responses is 0.02, 0.39, 0.36, 0.23

H 1 :   H 0 is false.        α=0.05

The formula for the test statistic is:

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=3,326 and the proportions specified in the null hypothesis are 0.02, 0.39, 0.36 and 0.23. Thus, min( 3326(0.02), 3326(0.39), 3326(0.36), 3326(0.23))=min(66.5, 1297.1, 1197.4, 765.0)=66.5. The sample size is more than adequate, so the formula can be used.

Here we have df=k-1=4-1=3 and a 5% level of significance. The appropriate critical value is 7.81 and the decision rule is as follows: Reject H 0 if χ 2 > 7.81.

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) into the formula for the test statistic identified in Step 2. We organize the computations in the following table.

The test statistic is computed as follows:

We reject H 0 because 233.53 > 7.81. We have statistically significant evidence at α=0.05 to show that H 0 is false or that the distribution of BMI in Framingham is different from the national data reported in 2002, p < 0.005.  

Again, the χ 2   goodness-of-fit test allows us to assess whether the distribution of responses "fits" a specified distribution. Here we show that the distribution of BMI in the Framingham Offspring Study is different from the national distribution. To understand the nature of the difference we can compare observed and expected frequencies or observed and expected proportions (or percentages). The frequencies are large because of the large sample size, the observed percentages of patients in the Framingham sample are as follows: 0.6% underweight, 28% normal weight, 41% overweight and 30% obese. In the Framingham Offspring sample there are higher percentages of overweight and obese persons (41% and 30% in Framingham as compared to 36% and 23% in the national data), and lower proportions of underweight and normal weight persons (0.6% and 28% in Framingham as compared to 2% and 39% in the national data). Are these meaningful differences?

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable in a single population. We presented a test using a test statistic Z to test whether an observed (sample) proportion differed significantly from a historical or external comparator. The chi-square goodness-of-fit test can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square goodness-of-fit test.

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

We presented the following approach to the test using a Z statistic. 

• Step 1. Set up hypotheses and determine level of significance

H 0 : p = 0.75

H 1 : p ≠ 0.75                               α=0.05

We must first check that the sample size is adequate. Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 125(0.75), 125(1-0.75))=min(94, 31)=31. The sample size is more than adequate so the following formula can be used

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. The sample proportion is:

We reject H 0 because -6.15 < -1.960. We have statistically significant evidence at a =0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001).  

We now conduct the same test using the chi-square goodness-of-fit test. First, we summarize our sample data as follows:

H 0 : p 1 =0.75, p 2 =0.25     or equivalently H 0 : Distribution of responses is 0.75, 0.25 

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ...,np k >) > 5. The sample size here is n=125 and the proportions specified in the null hypothesis are 0.75, 0.25. Thus, min( 125(0.75), 125(0.25))=min(93.75, 31.25)=31.25. The sample size is more than adequate so the formula can be used.

Here we have df=k-1=2-1=1 and a 5% level of significance. The appropriate critical value is 3.84, and the decision rule is as follows: Reject H 0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

(Note that (-6.15) 2 = 37.8, where -6.15 was the value of the Z statistic in the test for proportions shown above.)

We reject H 0 because 37.8 > 3.84. We have statistically significant evidence at α=0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data.  (p < 0.0001). This is the same conclusion we reached when we conducted the test using the Z test above. With a dichotomous outcome, Z 2 = χ 2 !   In statistics, there are often several approaches that can be used to test hypotheses. 

Tests for Two or More Independent Samples, Discrete Outcome

Here we extend that application of the chi-square test to the case with two or more independent comparison groups. Specifically, the outcome of interest is discrete with two or more responses and the responses can be ordered or unordered (i.e., the outcome can be dichotomous, ordinal or categorical). We now consider the situation where there are two or more independent comparison groups and the goal of the analysis is to compare the distribution of responses to the discrete outcome variable among several independent comparison groups.  

The test is called the χ 2 test of independence and the null hypothesis is that there is no difference in the distribution of responses to the outcome across comparison groups. This is often stated as follows: The outcome variable and the grouping variable (e.g., the comparison treatments or comparison groups) are independent (hence the name of the test). Independence here implies homogeneity in the distribution of the outcome among comparison groups.    

The null hypothesis in the χ 2 test of independence is often stated in words as: H 0 : The distribution of the outcome is independent of the groups. The alternative or research hypothesis is that there is a difference in the distribution of responses to the outcome variable among the comparison groups (i.e., that the distribution of responses "depends" on the group). In order to test the hypothesis, we measure the discrete outcome variable in each participant in each comparison group. The data of interest are the observed frequencies (or number of participants in each response category in each group). The formula for the test statistic for the χ 2 test of independence is given below.

Test Statistic for Testing H 0 : Distribution of outcome is independent of groups

and we find the critical value in a table of probabilities for the chi-square distribution with df=(r-1)*(c-1).

Here O = observed frequency, E=expected frequency in each of the response categories in each group, r = the number of rows in the two-way table and c = the number of columns in the two-way table.   r and c correspond to the number of comparison groups and the number of response options in the outcome (see below for more details). The observed frequencies are the sample data and the expected frequencies are computed as described below. The test statistic is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories in each group.  

The data for the χ 2 test of independence are organized in a two-way table. The outcome and grouping variable are shown in the rows and columns of the table. The sample table below illustrates the data layout. The table entries (blank below) are the numbers of participants in each group responding to each response category of the outcome variable.

Table - Possible outcomes are are listed in the columns; The groups being compared are listed in rows.

In the table above, the grouping variable is shown in the rows of the table; r denotes the number of independent groups. The outcome variable is shown in the columns of the table; c denotes the number of response options in the outcome variable. Each combination of a row (group) and column (response) is called a cell of the table. The table has r*c cells and is sometimes called an r x c ("r by c") table. For example, if there are 4 groups and 5 categories in the outcome variable, the data are organized in a 4 X 5 table. The row and column totals are shown along the right-hand margin and the bottom of the table, respectively. The total sample size, N, can be computed by summing the row totals or the column totals. Similar to ANOVA, N does not refer to a population size here but rather to the total sample size in the analysis. The sample data can be organized into a table like the above. The numbers of participants within each group who select each response option are shown in the cells of the table and these are the observed frequencies used in the test statistic.

The test statistic for the χ 2 test of independence involves comparing observed (sample data) and expected frequencies in each cell of the table. The expected frequencies are computed assuming that the null hypothesis is true. The null hypothesis states that the two variables (the grouping variable and the outcome) are independent. The definition of independence is as follows:

 Two events, A and B, are independent if P(A|B) = P(A), or equivalently, if P(A and B) = P(A) P(B).

The second statement indicates that if two events, A and B, are independent then the probability of their intersection can be computed by multiplying the probability of each individual event. To conduct the χ 2 test of independence, we need to compute expected frequencies in each cell of the table. Expected frequencies are computed by assuming that the grouping variable and outcome are independent (i.e., under the null hypothesis). Thus, if the null hypothesis is true, using the definition of independence:

P(Group 1 and Response Option 1) = P(Group 1) P(Response Option 1).

 The above states that the probability that an individual is in Group 1 and their outcome is Response Option 1 is computed by multiplying the probability that person is in Group 1 by the probability that a person is in Response Option 1. To conduct the χ 2 test of independence, we need expected frequencies and not expected probabilities . To convert the above probability to a frequency, we multiply by N. Consider the following small example.

The data shown above are measured in a sample of size N=150. The frequencies in the cells of the table are the observed frequencies. If Group and Response are independent, then we can compute the probability that a person in the sample is in Group 1 and Response category 1 using:

P(Group 1 and Response 1) = P(Group 1) P(Response 1),

P(Group 1 and Response 1) = (25/150) (62/150) = 0.069.

Thus if Group and Response are independent we would expect 6.9% of the sample to be in the top left cell of the table (Group 1 and Response 1). The expected frequency is 150(0.069) = 10.4.   We could do the same for Group 2 and Response 1:

P(Group 2 and Response 1) = P(Group 2) P(Response 1),

P(Group 2 and Response 1) = (50/150) (62/150) = 0.138.

The expected frequency in Group 2 and Response 1 is 150(0.138) = 20.7.

Thus, the formula for determining the expected cell frequencies in the χ 2 test of independence is as follows:

Expected Cell Frequency = (Row Total * Column Total)/N.

The above computes the expected frequency in one step rather than computing the expected probability first and then converting to a frequency.  

In a prior example we evaluated data from a survey of university graduates which assessed, among other things, how frequently they exercised. The survey was completed by 470 graduates. In the prior example we used the χ 2 goodness-of-fit test to assess whether there was a shift in the distribution of responses to the exercise question following the implementation of a health promotion campaign on campus. We specifically considered one sample (all students) and compared the observed distribution to the distribution of responses the prior year (a historical control). Suppose we now wish to assess whether there is a relationship between exercise on campus and students' living arrangements. As part of the same survey, graduates were asked where they lived their senior year. The response options were dormitory, on-campus apartment, off-campus apartment, and at home (i.e., commuted to and from the university). The data are shown below.

Based on the data, is there a relationship between exercise and student's living arrangement? Do you think where a person lives affect their exercise status? Here we have four independent comparison groups (living arrangement) and a discrete (ordinal) outcome variable with three response options. We specifically want to test whether living arrangement and exercise are independent. We will run the test using the five-step approach.  

H 0 : Living arrangement and exercise are independent

H 1 : H 0 is false.                α=0.05

The null and research hypotheses are written in words rather than in symbols. The research hypothesis is that the grouping variable (living arrangement) and the outcome variable (exercise) are dependent or related.   

• Step 2.  Select the appropriate test statistic.  

The condition for appropriate use of the above test statistic is that each expected frequency is at least 5. In Step 4 we will compute the expected frequencies and we will ensure that the condition is met.

The decision rule depends on the level of significance and the degrees of freedom, defined as df = (r-1)(c-1), where r and c are the numbers of rows and columns in the two-way data table.   The row variable is the living arrangement and there are 4 arrangements considered, thus r=4. The column variable is exercise and 3 responses are considered, thus c=3. For this test, df=(4-1)(3-1)=3(2)=6. Again, with χ 2 tests there are no upper, lower or two-tailed tests. If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. The rejection region for the χ 2 test of independence is always in the upper (right-hand) tail of the distribution. For df=6 and a 5% level of significance, the appropriate critical value is 12.59 and the decision rule is as follows: Reject H 0 if c 2 > 12.59.

We now compute the expected frequencies using the formula,

Expected Frequency = (Row Total * Column Total)/N.

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency.   The expected frequencies are shown in parentheses.

Notice that the expected frequencies are taken to one decimal place and that the sums of the observed frequencies are equal to the sums of the expected frequencies in each row and column of the table.  

Recall in Step 2 a condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 9.6) and therefore it is appropriate to use the test statistic.

We reject H 0 because 60.5 > 12.59. We have statistically significant evidence at a =0.05 to show that H 0 is false or that living arrangement and exercise are not independent (i.e., they are dependent or related), p < 0.005.  

Again, the χ 2 test of independence is used to test whether the distribution of the outcome variable is similar across the comparison groups. Here we rejected H 0 and concluded that the distribution of exercise is not independent of living arrangement, or that there is a relationship between living arrangement and exercise. The test provides an overall assessment of statistical significance. When the null hypothesis is rejected, it is important to review the sample data to understand the nature of the relationship. Consider again the sample data. 

Because there are different numbers of students in each living situation, it makes the comparisons of exercise patterns difficult on the basis of the frequencies alone. The following table displays the percentages of students in each exercise category by living arrangement. The percentages sum to 100% in each row of the table. For comparison purposes, percentages are also shown for the total sample along the bottom row of the table.

From the above, it is clear that higher percentages of students living in dormitories and in on-campus apartments reported regular exercise (31% and 23%) as compared to students living in off-campus apartments and at home (10% each).  

Test Yourself

 Pancreaticoduodenectomy (PD) is a procedure that is associated with considerable morbidity. A study was recently conducted on 553 patients who had a successful PD between January 2000 and December 2010 to determine whether their Surgical Apgar Score (SAS) is related to 30-day perioperative morbidity and mortality. The table below gives the number of patients experiencing no, minor, or major morbidity by SAS category.  

Question: What would be an appropriate statistical test to examine whether there is an association between Surgical Apgar Score and patient outcome? Using 14.13 as the value of the test statistic for these data, carry out the appropriate test at a 5% level of significance. Show all parts of your test.

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable and two independent comparison groups. We presented a test using a test statistic Z to test for equality of independent proportions. The chi-square test of independence can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square test of independence.

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We tested whether there was a significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using a Z statistic, as follows. 

H 0 : p 1 = p 2    

H 1 : p 1 ≠ p 2                             α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group or that:

In this example, we have

Therefore, the sample size is adequate, so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5.  Conclusion.  

We now conduct the same test using the chi-square test of independence.  

H 0 : Treatment and outcome (meaningful reduction in pain) are independent

H 1 :   H 0 is false.         α=0.05

The formula for the test statistic is:  

For this test, df=(2-1)(2-1)=1. At a 5% level of significance, the appropriate critical value is 3.84 and the decision rule is as follows: Reject H0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

We now compute the expected frequencies using:

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.

A condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 22.0) and therefore it is appropriate to use the test statistic.

(Note that (2.53) 2 = 6.4, where 2.53 was the value of the Z statistic in the test for proportions shown above.)

Chi-Squared Tests in R

The video below by Mike Marin demonstrates how to perform chi-squared tests in the R programming language.

Answer to Problem on Pancreaticoduodenectomy and Surgical Apgar Scores

We have 3 independent comparison groups (Surgical Apgar Score) and a categorical outcome variable (morbidity/mortality). We can run a Chi-Squared test of independence.

H 0 : Apgar scores and patient outcome are independent of one another.

H A : Apgar scores and patient outcome are not independent.

Chi-squared = 14.3

Since 14.3 is greater than 9.49, we reject H 0.

There is an association between Apgar scores and patient outcome. The lowest Apgar score group (0 to 4) experienced the highest percentage of major morbidity or mortality (16 out of 57=28%) compared to the other Apgar score groups.

Statistics Made Easy

Chi-Square Test of Independence: Definition, Formula, and Example

A Chi-Square Test of Independence  is used to determine whether or not there is a significant association between two categorical variables.

This tutorial explains the following:

• The motivation for performing a Chi-Square Test of Independence.
• The formula to perform a Chi-Square Test of Independence.
• An example of how to perform a Chi-Square Test of Independence.

Chi-Square Test of Independence: Motivation

A Chi-Square test of independence can be used to determine if there is an association between two categorical variables in a many different settings. Here are a few examples:

• We want to know if gender is associated with political party preference so we survey 500 voters and record their gender and political party preference.
• We want to know if a person’s favorite color is associated with their favorite sport so we survey 100 people and ask them about their preferences for both.
• We want to know if education level and marital status are associated so we collect data about these two variables on a simple random sample of 50 people.

In each of these scenarios we want to know if two categorical variables are associated with each other. In each scenario, we can use a Chi-Square test of independence to determine if there is a statistically significant association between the variables. 

Chi-Square Test of Independence: Formula

A Chi-Square test of independence uses the following null and alternative hypotheses:

• H 0 : (null hypothesis)  The two variables are independent.
• H 1 : (alternative hypothesis)  The two variables are not independent. (i.e. they are associated)

We use the following formula to calculate the Chi-Square test statistic X 2 :

X 2 = Σ(O-E) 2  / E

• Σ:  is a fancy symbol that means “sum”
• O:  observed value
• E:  expected value

If the p-value that corresponds to the test statistic X 2  with (#rows-1)*(#columns-1) degrees of freedom is less than your chosen significance level then you can reject the null hypothesis.

Chi-Square Test of Independence: Example

Suppose we want to know whether or not gender is associated with political party preference. We take a simple random sample of 500 voters and survey them on their political party preference. The following table shows the results of the survey:

Use the following steps to perform a Chi-Square test of independence to determine if gender is associated with political party preference.

Step 1: Define the hypotheses.

We will perform the Chi-Square test of independence using the following hypotheses:

• H 0 :  Gender and political party preference are independent.
• H 1 : Gender and political party preference are  not independent.

Step 2: Calculate the expected values.

Next, we will calculate the expected values for each cell in the contingency table using the following formula:

Expected value = (row sum * column sum) / table sum.

For example, the expected value for Male Republicans is: (230*250) / 500 =  115 .

We can repeat this formula to obtain the expected value for each cell in the table:

Step 3: Calculate (O-E) 2  / E for each cell in the table.

Next we will calculate  (O-E) 2  / E  for each cell in the table  where:

For example, Male Republicans would have a value of: (120-115) 2 /115 =  0.2174 .

We can repeat this formula for each cell in the table:

Step 4: Calculate the test statistic X 2  and the corresponding p-value.

X 2  = Σ(O-E) 2  / E = 0.2174 + 0.2174 + 0.0676 + 0.0676 + 0.1471 + 0.1471 =  0.8642

According to the Chi-Square Score to P Value Calculator , the p-value associated with X 2  = 0.8642 and (2-1)*(3-1) = 2 degrees of freedom is  0.649198 .

Step 5: Draw a conclusion.

Since this p-value is not less than 0.05, we fail to reject the null hypothesis. This means we do not have sufficient evidence to say that there is an association between gender and political party preference.

Note:  You can also perform this entire test by simply using the Chi-Square Test of Independence Calculator .

Additional Resources

The following tutorials explain how to perform a Chi-Square test of independence using different statistical programs:

How to Perform a Chi-Square Test of Independence in Stata How to Perform a Chi-Square Test of Independence in Excel How to Perform a Chi-Square Test of Independence in SPSS How to Perform a Chi-Square Test of Independence in Python How to Perform a Chi-Square Test of Independence in R Chi-Square Test of Independence on a TI-84 Calculator Chi-Square Test of Independence Calculator

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Chi-Square (Χ²) Test & How To Calculate Formula Equation

Benjamin Frimodig

Science Expert

B.A., History and Science, Harvard University

Ben Frimodig is a 2021 graduate of Harvard College, where he studied the History of Science.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

On This Page:

Chi-square (χ2) is used to test hypotheses about the distribution of observations into categories with no inherent ranking.

What Is a Chi-Square Statistic?

The Chi-square test (pronounced Kai) looks at the pattern of observations and will tell us if certain combinations of the categories occur more frequently than we would expect by chance, given the total number of times each category occurred.

It looks for an association between the variables. We cannot use a correlation coefficient to look for the patterns in this data because the categories often do not form a continuum.

There are three main types of Chi-square tests, tests of goodness of fit, the test of independence, and the test for homogeneity. All three tests rely on the same formula to compute a test statistic.

These tests function by deciphering relationships between observed sets of data and theoretical or “expected” sets of data that align with the null hypothesis.

What is a Contingency Table?

Contingency tables (also known as two-way tables) are grids in which Chi-square data is organized and displayed. They provide a basic picture of the interrelation between two variables and can help find interactions between them.

In contingency tables, one variable and each of its categories are listed vertically, and the other variable and each of its categories are listed horizontally.

Additionally, including column and row totals, also known as “marginal frequencies,” will help facilitate the Chi-square testing process.

In order for the Chi-square test to be considered trustworthy, each cell of your expected contingency table must have a value of at least five.

Each Chi-square test will have one contingency table representing observed counts (see Fig. 1) and one contingency table representing expected counts (see Fig. 2).

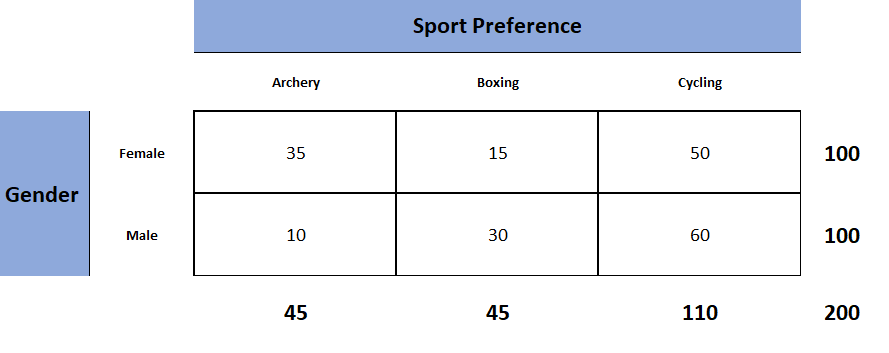
Figure 1. Observed table (which contains the observed counts).

To obtain the expected frequencies for any cell in any cross-tabulation in which the two variables are assumed independent, multiply the row and column totals for that cell and divide the product by the total number of cases in the table.

Figure 2. Expected table (what we expect the two-way table to look like if the two categorical variables are independent).

To decide if our calculated value for χ2 is significant, we also need to work out the degrees of freedom for our contingency table using the following formula: df= (rows – 1) x (columns – 1).

Formula Calculation

Calculate the chi-square statistic (χ2) by completing the following steps:

• Calculate the expected frequencies and the observed frequencies.
• For each observed number in the table, subtract the corresponding expected number (O — E).
• Square the difference (O —E)².
• Divide the squares obtained for each cell in the table by the expected number for that cell (O – E)² / E.
• Sum all the values for (O – E)² / E. This is the chi-square statistic.
• Calculate the degrees of freedom for the contingency table using the following formula; df= (rows – 1) x (columns – 1).

Once we have calculated the degrees of freedom (df) and the chi-squared value (χ2), we can use the χ2 table (often at the back of a statistics book) to check if our value for χ2 is higher than the critical value given in the table. If it is, then our result is significant at the level given.

Interpretation

The chi-square statistic tells you how much difference exists between the observed count in each table cell to the counts you would expect if there were no relationship at all in the population.

Small Chi-Square Statistic: If the chi-square statistic is small and the p-value is large (usually greater than 0.05), this often indicates that the observed frequencies in the sample are close to what would be expected under the null hypothesis.

The null hypothesis usually states no association between the variables being studied or that the observed distribution fits the expected distribution.

In theory, if the observed and expected values were equal (no difference), then the chi-square statistic would be zero — but this is unlikely to happen in real life.

Large Chi-Square Statistic : If the chi-square statistic is large and the p-value is small (usually less than 0.05), then the conclusion is often that the data does not fit the model well, i.e., the observed and expected values are significantly different. This often leads to the rejection of the null hypothesis.

How to Report

To report a chi-square output in an APA-style results section, always rely on the following template:

χ2 ( degrees of freedom , N = sample size ) = chi-square statistic value , p = p value .

In the case of the above example, the results would be written as follows:

A chi-square test of independence showed that there was a significant association between gender and post-graduation education plans, χ2 (4, N = 101) = 54.50, p < .001.

APA Style Rules

• Do not use a zero before a decimal when the statistic cannot be greater than 1 (proportion, correlation, level of statistical significance).
• Report exact p values to two or three decimals (e.g., p = .006, p = .03).
• However, report p values less than .001 as “ p < .001.”
• Put a space before and after a mathematical operator (e.g., minus, plus, greater than, less than, equals sign).
• Do not repeat statistics in both the text and a table or figure.

p -value Interpretation

You test whether a given χ2 is statistically significant by testing it against a table of chi-square distributions , according to the number of degrees of freedom for your sample, which is the number of categories minus 1. The chi-square assumes that you have at least 5 observations per category.

If you are using SPSS then you will have an expected p -value.

For a chi-square test, a p-value that is less than or equal to the .05 significance level indicates that the observed values are different to the expected values.

Thus, low p-values (p< .05) indicate a likely difference between the theoretical population and the collected sample. You can conclude that a relationship exists between the categorical variables.

Remember that p -values do not indicate the odds that the null hypothesis is true but rather provide the probability that one would obtain the sample distribution observed (or a more extreme distribution) if the null hypothesis was true.

A level of confidence necessary to accept the null hypothesis can never be reached. Therefore, conclusions must choose to either fail to reject the null or accept the alternative hypothesis, depending on the calculated p-value.

The four steps below show you how to analyze your data using a chi-square goodness-of-fit test in SPSS (when you have hypothesized that you have equal expected proportions).

Step 1 : Analyze > Nonparametric Tests > Legacy Dialogs > Chi-square… on the top menu as shown below:

Step 2 : Move the variable indicating categories into the “Test Variable List:” box.

Step 3 : If you want to test the hypothesis that all categories are equally likely, click “OK.”

Step 4 : Specify the expected count for each category by first clicking the “Values” button under “Expected Values.”

Step 5 : Then, in the box to the right of “Values,” enter the expected count for category one and click the “Add” button. Now enter the expected count for category two and click “Add.” Continue in this way until all expected counts have been entered.

Step 6 : Then click “OK.”

The four steps below show you how to analyze your data using a chi-square test of independence in SPSS Statistics.

Step 1 : Open the Crosstabs dialog (Analyze > Descriptive Statistics > Crosstabs).

Step 2 : Select the variables you want to compare using the chi-square test. Click one variable in the left window and then click the arrow at the top to move the variable. Select the row variable and the column variable.

Step 3 : Click Statistics (a new pop-up window will appear). Check Chi-square, then click Continue.

Step 4 : (Optional) Check the box for Display clustered bar charts.

Step 5 : Click OK.

Goodness-of-Fit Test

The Chi-square goodness of fit test is used to compare a randomly collected sample containing a single, categorical variable to a larger population.

This test is most commonly used to compare a random sample to the population from which it was potentially collected.

The test begins with the creation of a null and alternative hypothesis. In this case, the hypotheses are as follows:

Null Hypothesis (Ho) : The null hypothesis (Ho) is that the observed frequencies are the same (except for chance variation) as the expected frequencies. The collected data is consistent with the population distribution.

Alternative Hypothesis (Ha) : The collected data is not consistent with the population distribution.

The next step is to create a contingency table that represents how the data would be distributed if the null hypothesis were exactly correct.

The sample’s overall deviation from this theoretical/expected data will allow us to draw a conclusion, with a more severe deviation resulting in smaller p-values.

Test for Independence

The Chi-square test for independence looks for an association between two categorical variables within the same population.

Unlike the goodness of fit test, the test for independence does not compare a single observed variable to a theoretical population but rather two variables within a sample set to one another.

The hypotheses for a Chi-square test of independence are as follows:

Null Hypothesis (Ho) : There is no association between the two categorical variables in the population of interest.

Alternative Hypothesis (Ha) : There is no association between the two categorical variables in the population of interest.

The next step is to create a contingency table of expected values that reflects how a data set that perfectly aligns the null hypothesis would appear.

The simplest way to do this is to calculate the marginal frequencies of each row and column; the expected frequency of each cell is equal to the marginal frequency of the row and column that corresponds to a given cell in the observed contingency table divided by the total sample size.

Test for Homogeneity

The Chi-square test for homogeneity is organized and executed exactly the same as the test for independence.

The main difference to remember between the two is that the test for independence looks for an association between two categorical variables within the same population, while the test for homogeneity determines if the distribution of a variable is the same in each of several populations (thus allocating population itself as the second categorical variable).

Null Hypothesis (Ho) : There is no difference in the distribution of a categorical variable for several populations or treatments.

Alternative Hypothesis (Ha) : There is a difference in the distribution of a categorical variable for several populations or treatments.

The difference between these two tests can be a bit tricky to determine, especially in the practical applications of a Chi-square test. A reliable rule of thumb is to determine how the data was collected.

If the data consists of only one random sample with the observations classified according to two categorical variables, it is a test for independence. If the data consists of more than one independent random sample, it is a test for homogeneity.

What is the chi-square test?

The Chi-square test is a non-parametric statistical test used to determine if there’s a significant association between two or more categorical variables in a sample.

It works by comparing the observed frequencies in each category of a cross-tabulation with the frequencies expected under the null hypothesis, which assumes there is no relationship between the variables.

This test is often used in fields like biology, marketing, sociology, and psychology for hypothesis testing.

What does chi-square tell you?

The Chi-square test informs whether there is a significant association between two categorical variables. Suppose the calculated Chi-square value is above the critical value from the Chi-square distribution.

In that case, it suggests a significant relationship between the variables, rejecting the null hypothesis of no association.

How to calculate chi-square?

To calculate the Chi-square statistic, follow these steps:

1. Create a contingency table of observed frequencies for each category.

2. Calculate expected frequencies for each category under the null hypothesis.

3. Compute the Chi-square statistic using the formula: Χ² = Σ [ (O_i – E_i)² / E_i ], where O_i is the observed frequency and E_i is the expected frequency.

4. Compare the calculated statistic with the critical value from the Chi-square distribution to draw a conclusion.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.1: Chi-Square Tests for Independence

• Last updated
• Save as PDF
• Page ID 513

Learning Objectives

• To understand what chi-square distributions are.
• To understand how to use a chi-square test to judge whether two factors are independent.

Chi-Square Distributions

As you know, there is a whole family of \(t\)-distributions, each one specified by a parameter called the degrees of freedom, denoted \(df\). Similarly, all the chi-square distributions form a family, and each of its members is also specified by a parameter \(df\), the number of degrees of freedom. Chi is a Greek letter denoted by the symbol \(\chi\) and chi-square is often denoted by \(\chi^2\).

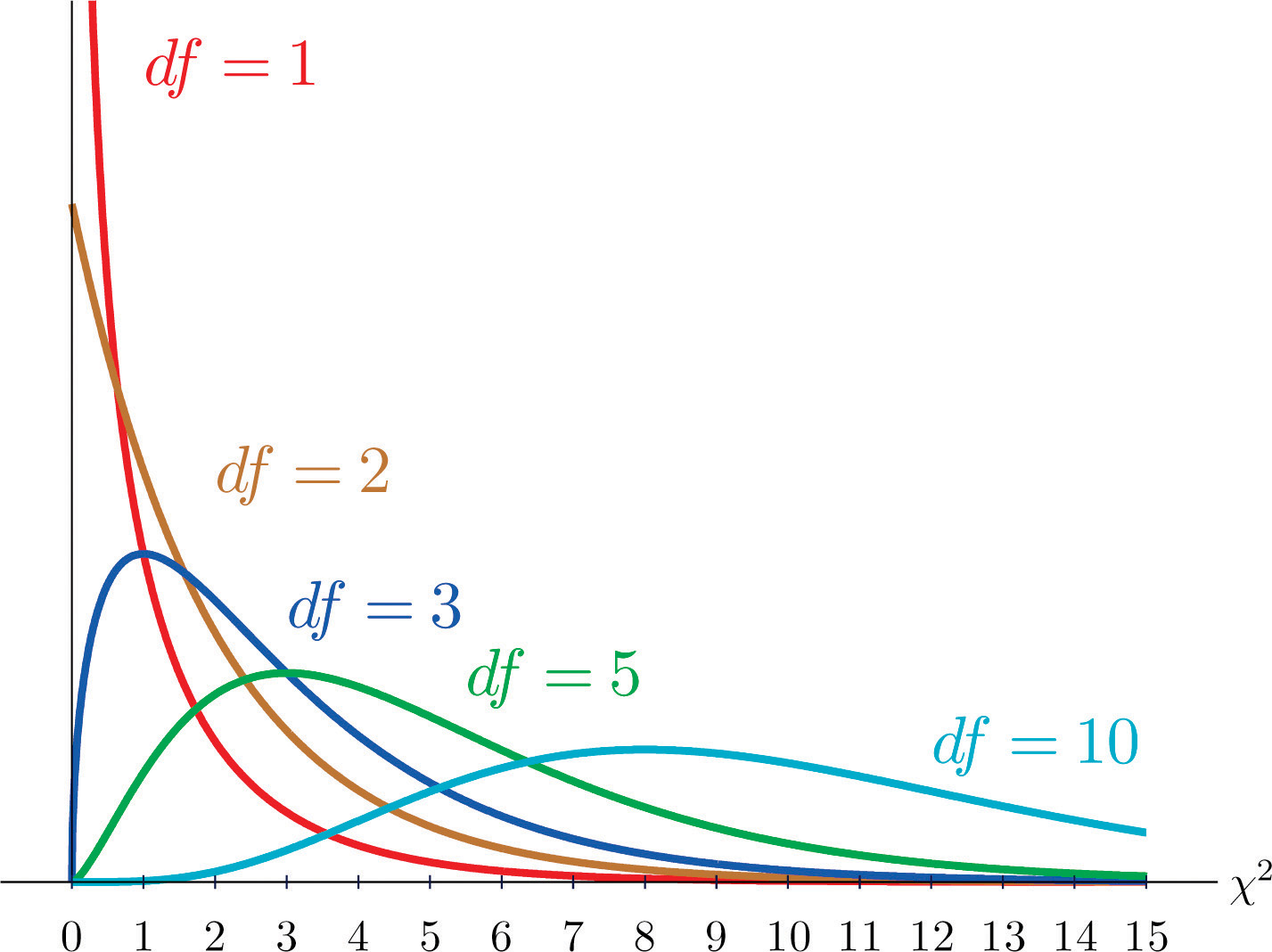
Figure \(\PageIndex{1}\) shows several \(\chi\)-square distributions for different degrees of freedom. A chi-square random variable is a random variable that assumes only positive values and follows a \(\chi\)-square distribution.

Definition: critical value

The value of the chi-square random variable \(\chi^2\) with \(df=k\) that cuts off a right tail of area \(c\) is denoted \(\chi_c^2\) and is called a critical value (Figure \(\PageIndex{2}\)).

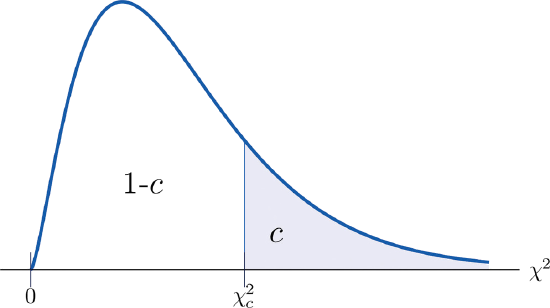
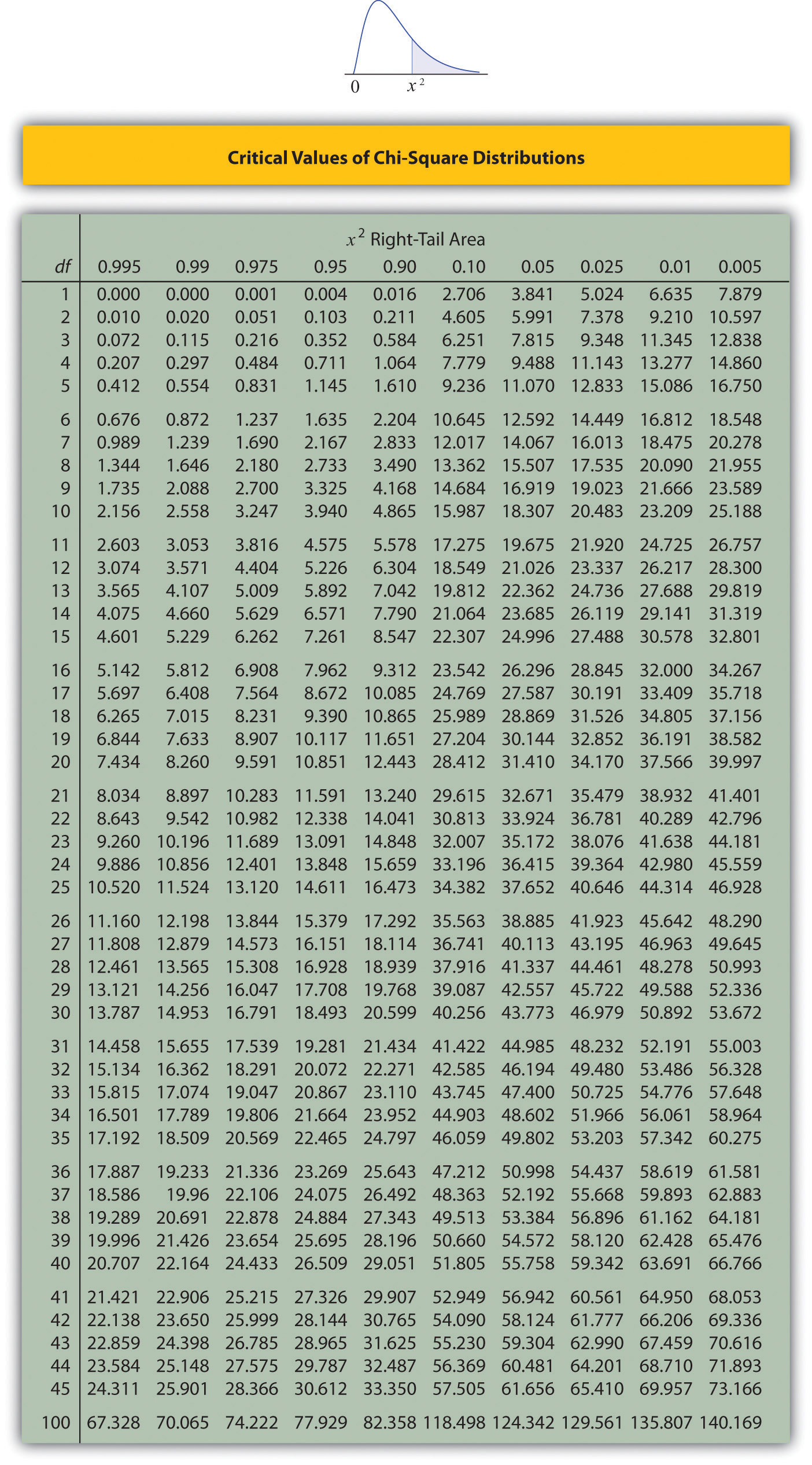
Figure \(\PageIndex{3}\) below gives values of \(\chi_c^2\) for various values of \(c\) and under several chi-square distributions with various degrees of freedom.

Tests for Independence

Hypotheses tests encountered earlier in the book had to do with how the numerical values of two population parameters compared. In this subsection we will investigate hypotheses that have to do with whether or not two random variables take their values independently, or whether the value of one has a relation to the value of the other. Thus the hypotheses will be expressed in words, not mathematical symbols. We build the discussion around the following example.

There is a theory that the gender of a baby in the womb is related to the baby’s heart rate: baby girls tend to have higher heart rates. Suppose we wish to test this theory. We examine the heart rate records of \(40\) babies taken during their mothers’ last prenatal checkups before delivery, and to each of these \(40\) randomly selected records we compute the values of two random measures: 1) gender and 2) heart rate. In this context these two random measures are often called factors. Since the burden of proof is that heart rate and gender are related, not that they are unrelated, the problem of testing the theory on baby gender and heart rate can be formulated as a test of the following hypotheses:

\[H_0: \text{Baby gender and baby heart rate are independent}\\ vs. \\ H_a: \text{Baby gender and baby heart rate are not independent} \nonumber \]

The factor gender has two natural categories or levels: boy and girl. We divide the second factor, heart rate, into two levels, low and high, by choosing some heart rate, say \(145\) beats per minute, as the cutoff between them. A heart rate below \(145\) beats per minute will be considered low and \(145\) and above considered high. The \(40\) records give rise to a \(2\times 2\) contingency table . By adjoining row totals, column totals, and a grand total we obtain the table shown as Table \(\PageIndex{1}\). The four entries in boldface type are counts of observations from the sample of \(n = 40\). There were \(11\) girls with low heart rate, \(17\) boys with low heart rate, and so on. They form the core of the expanded table.

In analogy with the fact that the probability of independent events is the product of the probabilities of each event, if heart rate and gender were independent then we would expect the number in each core cell to be close to the product of the row total \(R\) and column total \(C\) of the row and column containing it, divided by the sample size \(n\). Denoting such an expected number of observations \(E\), these four expected values are:

• 1 st row and 1 st column: \(E=(R\times C)/n = 18\times 28 /40 = 12.6\)
• 1 st row and 2 nd column: \(E=(R\times C)/n = 18\times 12 /40 = 5.4\)
• 2 nd row and 1 st column: \(E=(R\times C)/n = 22\times 28 /40 = 15.4\)
• 2 nd row and 2 nd column: \(E=(R\times C)/n = 22\times 12 /40 = 6.6\)

We update Table \(\PageIndex{1}\) by placing each expected value in its corresponding core cell, right under the observed value in the cell. This gives the updated table Table \(\PageIndex{2}\).

A measure of how much the data deviate from what we would expect to see if the factors really were independent is the sum of the squares of the difference of the numbers in each core cell, or, standardizing by dividing each square by the expected number in the cell, the sum \(\sum (O-E)^2 / E\). We would reject the null hypothesis that the factors are independent only if this number is large, so the test is right-tailed. In this example the random variable \(\sum (O-E)^2 / E\) has the chi-square distribution with one degree of freedom. If we had decided at the outset to test at the \(10\%\) level of significance, the critical value defining the rejection region would be, reading from Figure \(\PageIndex{3}\), \(\chi _{\alpha }^{2}=\chi _{0.10 }^{2}=2.706\), so that the rejection region would be the interval \([2.706,\infty )\). When we compute the value of the standardized test statistic we obtain

\[\sum \frac{(O-E)^2}{E}=\frac{(11-12.6)^2}{12.6}+\frac{(7-5.4)^2}{5.4}+\frac{(17-15.4)^2}{15.4}+\frac{(5-6.6)^2}{6.6}=1.231 \nonumber \]

Since \(1.231 < 2.706\), the decision is not to reject \(H_0\). See Figure \(\PageIndex{4}\). The data do not provide sufficient evidence, at the \(10\%\) level of significance, to conclude that heart rate and gender are related.

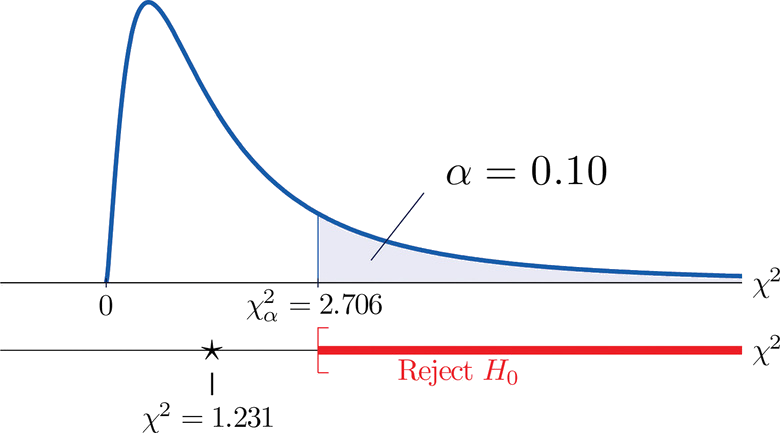
Fig ure \(\PageIndex{4}\) : Baby Gender Prediction

H 0 vs .   H a : : Baby   gender   and   baby   heart   rate   are   independent Baby   gender   and   baby   heart   rate   are   n o t   independent H 0 vs .   H a : : Baby   gender   and   baby   heart   rate   are   independent Baby   gender   and   baby   heart   rate   are   n o t   independent

With this specific example in mind, now turn to the general situation. In the general setting of testing the independence of two factors, call them Factor \(1\) and Factor \(2\), the hypotheses to be tested are

\[H_0: \text{The two factors are independent}\\ vs. \\ H_a: \text{The two factors are not independent} \nonumber \]

As in the example each factor is divided into a number of categories or levels. These could arise naturally, as in the boy-girl division of gender, or somewhat arbitrarily, as in the high-low division of heart rate. Suppose Factor \(1\) has \(I\) levels and Factor \(2\) has \(J\) levels. Then the information from a random sample gives rise to a general \(I\times J\) contingency table, which with row totals, column totals, and a grand total would appear as shown in Table \(\PageIndex{3}\). Each cell may be labeled by a pair of indices \((i,j)\). \(O_{ij}\) stands for the observed count of observations in the cell in row \(i\) and column \(j\), \(R_i\) for the \(i^{th}\) row total and \(C_j\) for the \(j^{th}\) column total. To simplify the notation we will drop the indices so Table \(\PageIndex{3}\) becomes Table \(\PageIndex{4}\). Nevertheless it is important to keep in mind that the \(Os\), the \(Rs\) and the \(Cs\), though denoted by the same symbols, are in fact different numbers.

As in the example, for each core cell in the table we compute what would be the expected number \(E\) of observations if the two factors were independent. \(E\) is computed for each core cell (each cell with an \(O\) in it) of Table \(\PageIndex{4}\) by the rule applied in the example:

\[E=R×Cn \nonumber \]

where \(R\) is the row total and \(C\) is the column total corresponding to the cell, and \(n\) is the sample size

Here is the test statistic for the general hypothesis based on Table \(\PageIndex{5}\), together with the conditions that it follow a chi-square distribution.

Test Statistic for Testing the Independence of Two Factors

\[\chi^2=\sum (O−E)^2E \nonumber \]

where the sum is over all core cells of the table.

• the two study factors are independent, and
• the observed count \(O\) of each cell in Table \(\PageIndex{5}\) is at least \(5\),

then \(\chi ^2\) approximately follows a chi-square distribution with \(df=(I-1)\times (J-1)\) degrees of freedom.

The same five-step procedures, either the critical value approach or the \(p\)-value approach, that were introduced in Section 8.1 and Section 8.3 are used to perform the test, which is always right-tailed.

Example \(\PageIndex{1}\)

A researcher wishes to investigate whether students’ scores on a college entrance examination (\(CEE\)) have any indicative power for future college performance as measured by \(GPA\). In other words, he wishes to investigate whether the factors \(CEE\) and \(GPA\) are independent or not. He randomly selects \(n = 100\) students in a college and notes each student’s score on the entrance examination and his grade point average at the end of the sophomore year. He divides entrance exam scores into two levels and grade point averages into three levels. Sorting the data according to these divisions, he forms the contingency table shown as Table \(\PageIndex{6}\), in which the row and column totals have already been computed.

Test, at the \(1\%\) level of significance, whether these data provide sufficient evidence to conclude that \(CEE\) scores indicate future performance levels of incoming college freshmen as measured by \(GPA\).

We perform the test using the critical value approach, following the usual five-step method outlined at the end of Section 8.1.

• Step 1 . The hypotheses are \[H_0:\text{CEE and GPA are independent factors}\\ vs.\\ H_a:\text{CEE and GPA are not independent factors} \nonumber \]
• Step 2 . The distribution is chi-square.
• 1 st row and 1 st column: \(E=(R\times C)/n=41\times 52/100=21.32\)
• 1 st row and 2 nd column: \(E=(R\times C)/n=36\times 52/100=18.72\)
• 1 st row and 3 rd column: \(E=(R\times C)/n=23\times 52/100=11.96\)
• 2 nd row and 1 st column: \(E=(R\times C)/n=41\times 48/100=19.68\)
• 2 nd row and 2 nd column: \(E=(R\times C)/n=36\times 48/100=17.28\)
• 2 nd row and 3 rd column: \(E=(R\times C)/n=23\times 48/100=11.04\)

Table \(\PageIndex{6}\) is updated to Table \(\PageIndex{6}\).

The test statistic is

\[\begin{align*} \chi^2 &= \sum \frac{(O-E)^2}{E}\\ &= \frac{(35-21.32)^2}{21.32}+\frac{(12-18.72)^2}{18.72}+\frac{(5-11.96)^2}{11.96}+\frac{(6-19.68)^2}{19.68}+\frac{(24-17.28)^2}{17.28}+\frac{(18-11.04)^2}{11.04}\\ &= 31.75 \end{align*} \nonumber \]

• Step 4 . Since the \(CEE\) factor has two levels and the \(GPA\) factor has three, \(I = 2\) and \(J = 3\). Thus the test statistic follows the chi-square distribution with \(df=(2-1)\times (3-1)=2\) degrees of freedom.

Since the test is right-tailed, the critical value is \(\chi _{0.01}^{2}\). Reading from Figure 7.1.6 "Critical Values of Chi-Square Distributions", \(\chi _{0.01}^{2}=9.210\), so the rejection region is \([9.210,\infty )\).

• Step 5 . Since \(31.75 > 9.21\) the decision is to reject the null hypothesis. See Figure \(\PageIndex{5}\). The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that \(CEE\) score and \(GPA\) are not independent: the entrance exam score has predictive power.

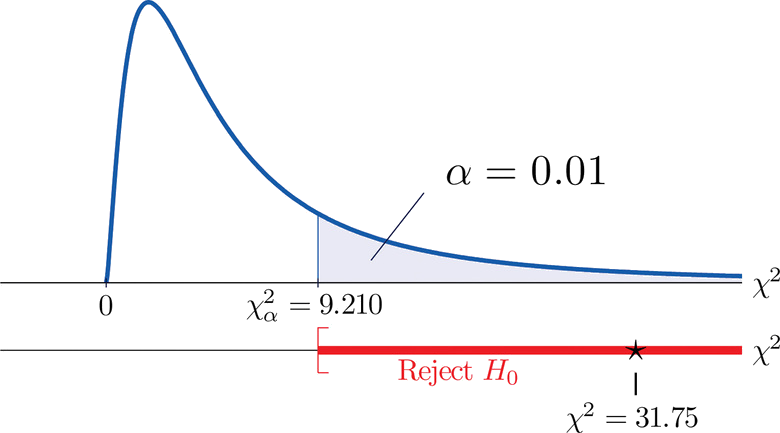
Key Takeaway

• Critical values of a chi-square distribution with degrees of freedom df are found in Figure 7.1.6.
• A chi-square test can be used to evaluate the hypothesis that two random variables or factors are independent.

8. The Chi squared tests

The χ²tests.

The p-value can be found using Minitab. Look up the area to the right of your chi-square test statistic on a chi-square distribution with the correct degrees of freedom. Chi-square tests are always right-tailed tests. 

If \(p \leq \alpha\) reject the null hypothesis.

If \(p>\alpha\) fail to reject the null hypothesis.

Write a conclusion in terms of the original research question.

11.3.1 - Example: Gender and Online Learning

Gender and online learning.

A sample of 314 Penn State students was asked if they have ever taken an online course. Their genders were also recorded. The contingency table below was constructed. Use a chi-square test of independence to determine if there is a relationship between gender and whether or not someone has taken an online course.

\(H_0:\) There is not a relationship between gender and whether or not someone has taken an online course (they are independent)

\(H_a:\) There is a relationship between gender and whether or not someone has taken an online course (they are dependent)

Looking ahead to our calculations of the expected values, we can see that all expected values are at least 5. This means that the sampling distribution can be approximated using the \(\chi^2\) distribution. 

In order to compute the chi-square test statistic we must know the observed and expected values for each cell. We are given the observed values in the table above. We must compute the expected values. The table below includes the row and column totals.

Note that all expected values are at least 5, thus this assumption of the \(\chi^2\) test of independence has been met. 

Observed and expected counts are often presented together in a contingency table. In the table below, expected values are presented in parentheses.

\(\chi^2=\sum \dfrac{(O-E)^2}{E} \)

\(\chi^2=\dfrac{(43-46.586)^2}{46.586}+\dfrac{(63-59.414)^2}{59.414}+\dfrac{(95-91.414)^2}{91.414}+\dfrac{(113-116.586)^2}{116.586}=0.276+0.216+0.141+0.110=0.743\)

The chi-square test statistic is 0.743

\(df=(number\;of\;rows-1)(number\;of\;columns-1)=(2-1)(2-1)=1\)

We can determine the p-value by constructing a chi-square distribution plot with 1 degree of freedom and finding the area to the right of 0.743.

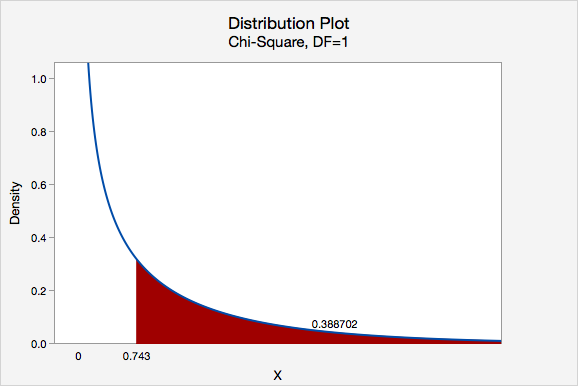
\(p = 0.388702\)

\(p>\alpha\), therefore we fail to reject the null hypothesis.

There is not enough evidence to conclude that gender and whether or not an individual has completed an online course are related.

Note that we cannot say for sure that these two categorical variables are independent, we can only say that we do not have enough evidence that they are dependent.

11.3.2 - Minitab: Test of Independence

Raw vs summarized data.

If you have a data file with the responses for individual cases then you have "raw data" and can follow the directions below. If you have a table filled with data, then you have "summarized data." There is an example of conducting a chi-square test of independence using summarized data on a later page. After data entry the procedure is the same for both data entry methods.

Minitab ®  – Chi-square Test Using Raw Data

Research question : Is there a relationship between where a student sits in class and whether they have ever cheated?

• Null hypothesis : Seat location and cheating are not related in the population. 
• Alternative hypothesis : Seat location and cheating are related in the population.

To perform a chi-square test of independence in Minitab using raw data:

• Open Minitab file: class_survey.mpx
• Select Stat > Tables > Chi-Square Test for Association
• Select Raw data (categorical variables) from the dropdown.
• Choose the variable  Seating  to insert it into the  Rows  box
• Choose the variable  Ever_Cheat  to insert it into the  Columns  box
• Click the Statistics button and check the boxes  Chi-square test for association  and  Expected cell counts
• Click  OK and OK

This should result in the following output:

Rows: Seating Columns: Ever_Cheat

Chi-square test.

All expected values are at least 5 so we can use the Pearson chi-square test statistic. Our results are \(\chi^2 (2) = 1.539\). \(p = 0.463\). Because our \(p\) value is greater than the standard alpha level of 0.05, we fail to reject the null hypothesis. There is not enough evidence of a relationship in the population between seat location and whether a student has cheated.

11.3.2.1 - Example: Raw Data

Example: dog & cat ownership.

Is there a relationship between dog and cat ownership in the population of all World Campus STAT 200 students? Let's conduct an hypothesis test using the dataset: fall2016stdata.mpx

 \(H_0:\) There is not a relationship between dog ownership and cat ownership in the population of all World Campus STAT 200 students \(H_a:\) There is a relationship between dog ownership and cat ownership in the population of all World Campus STAT 200 students

Assumption: All expected counts are at least 5. The expected counts here are 176.02, 75.98, 189.98, and 82.02, so this assumption has been met.

Let's use Minitab to calculate the test statistic and p-value.

• After entering the data, select Stat > Tables > Cross Tabulation and Chi-Square
• Enter Dog in the Rows box
• Enter Cat in the Columns box
• Select the Chi-Square button and in the new window check the box for the Chi-square test and Expected cell counts

Rows: Dog Columns: Cat

Since the assumption was met in step 1, we can use the Pearson chi-square test statistic.

\(Pearson\;\chi^2 = 1.771\)

\(p = 0.183\)

Our p value is greater than the standard 0.05 alpha level, so we fail to reject the null hypothesis.

There is not enough evidence of a relationship between dog ownership and cat ownership in the population of all World Campus STAT 200 students.

11.3.2.2 - Example: Summarized Data

Example: coffee and tea preference.

Is there a relationship between liking tea and liking coffee?

The following table shows data collected from a random sample of 100 adults. Each were asked if they liked coffee (yes or no) and if they liked tea (yes or no).

Let's use the 5 step hypothesis testing procedure to address this research question.

 \(H_0:\) Liking coffee an liking tea are not related (i.e., independent) in the population \(H_a:\) Liking coffee and liking tea are related (i.e., dependent) in the population

Assumption: All expected counts are at least 5.

• Select Stat > Tables > Cross Tabulation and Chi-Square
• Select Summarized data in a two-way table from the dropdown
• Enter the columns Likes Coffee-Yes and Likes Coffee-No in the Columns containing the table box
• For the row labels enter Likes Tea (leave the column labels blank)
• Select the Chi-Square button and check the boxes for Chi-square test and Expected cell counts .

Rows: Likes Tea  Columns: Worksheet columns

\(Pearson\;\chi^2 = 10.774\)

\(p = 0.001\)

Our p value is less than the standard 0.05 alpha level, so we reject the null hypothesis.

There is evidence of a relationship between between liking coffee and liking tea in the population.

11.3.3 - Relative Risk

A chi-square test of independence will give you information concerning whether or not a relationship between two categorical variables in the population is likely. As was the case with the single sample and two sample hypothesis tests that you learned earlier this semester, with a large sample size statistical power is high and the probability of rejecting the null hypothesis is high, even if the relationship is relatively weak. In addition to examining statistical significance by looking at the p value, we can also examine practical significance by computing the  relative risk .

In Lesson 2 you learned that risk is often used to describe the probability of an event occurring. Risk can also be used to compare the probabilities in two different groups. First, we'll review risk, then you'll be introduced to the concept of relative risk.

The  risk  of an outcome can be expressed as a fraction or as the percent of a group that experiences the outcome.

Examples of Risk

60 out of 1000 teens have asthma. The risk is \(\frac{60}{1000}=.06\). This means that 6% of all teens experience asthma.

45 out of 100 children get the flu each year. The risk is \(\frac{45}{100}=.45\) or 45%

Thus, relative risk gives the risk for group 1 as a multiple of the risk for group 2.

Example of Relative Risk

Suppose that the risk of a child getting the flu this year is .45 and the risk of an adult getting the flu this year is .10. What is the relative risk of children compared to adults?

• \(Relative\;risk=\dfrac{.45}{.10}=4.5\)

Children are 4.5 times more likely than adults to get the flu this year.

Watch out for relative risk statistics where no baseline information is given about the actual risk. For instance, it doesn't mean much to say that beer drinkers have twice the risk of stomach cancer as non-drinkers unless we know the actual risks. The risk of stomach cancer might actually be very low, even for beer drinkers. For example, 2 in a million is twice the size of 1 in a million but is would still be a very low risk. This is known as the  baseline  with which other risks are compared.

• Flashes Safe Seven
• FlashLine Login
• Faculty & Staff Phone Directory
• Emeriti or Retiree
• All Departments
• Maps & Directions

• Building Guide
• Departments
• Directions & Parking
• Faculty & Staff
• Give to University Libraries
• Library Instructional Spaces
• Mission & Vision
• Newsletters
• Circulation
• Course Reserves / Core Textbooks
• Equipment for Checkout
• Interlibrary Loan
• Library Instruction
• Library Tutorials
• My Library Account
• Open Access Kent State
• Research Support Services
• Statistical Consulting
• Student Multimedia Studio
• Citation Tools
• Databases A-to-Z
• Databases By Subject
• Digital Collections
• Discovery@Kent State
• Government Information
• Journal Finder
• Library Guides
• Connect from Off-Campus
• Library Workshops
• Subject Librarians Directory
• Suggestions/Feedback
• Writing Commons
• Academic Integrity
• Jobs for Students
• International Students
• Meet with a Librarian
• Study Spaces
• University Libraries Student Scholarship
• Affordable Course Materials
• Copyright Services
• Selection Manager
• Suggest a Purchase

Library Locations at the Kent Campus

• Architecture Library
• Fashion Library
• Map Library
• Performing Arts Library
• Special Collections and Archives

Regional Campus Libraries

• East Liverpool
• College of Podiatric Medicine

• Kent State University
• SPSS Tutorials

Chi-Square Test of Independence

Spss tutorials: chi-square test of independence.

• The SPSS Environment
• The Data View Window
• Using SPSS Syntax
• Data Creation in SPSS
• Importing Data into SPSS
• Variable Types
• Date-Time Variables in SPSS
• Defining Variables
• Creating a Codebook
• Computing Variables
• Recoding Variables
• Recoding String Variables (Automatic Recode)
• Weighting Cases
• rank transform converts a set of data values by ordering them from smallest to largest, and then assigning a rank to each value. In SPSS, the Rank Cases procedure can be used to compute the rank transform of a variable." href="https://libguides.library.kent.edu/SPSS/RankCases" style="" >Rank Cases
• Sorting Data
• Grouping Data
• Descriptive Stats for One Numeric Variable (Explore)
• Descriptive Stats for One Numeric Variable (Frequencies)
• Descriptive Stats for Many Numeric Variables (Descriptives)
• Descriptive Stats by Group (Compare Means)
• Frequency Tables
• Working with "Check All That Apply" Survey Data (Multiple Response Sets)
• Pearson Correlation
• One Sample t Test
• Paired Samples t Test
• Independent Samples t Test
• One-Way ANOVA
• How to Cite the Tutorials

Sample Data Files

Our tutorials reference a dataset called "sample" in many examples. If you'd like to download the sample dataset to work through the examples, choose one of the files below:

• Data definitions (*.pdf)
• Data - Comma delimited (*.csv)
• Data - Tab delimited (*.txt)
• Data - Excel format (*.xlsx)
• Data - SAS format (*.sas7bdat)
• Data - SPSS format (*.sav)
• SPSS Syntax (*.sps) Syntax to add variable labels, value labels, set variable types, and compute several recoded variables used in later tutorials.
• SAS Syntax (*.sas) Syntax to read the CSV-format sample data and set variable labels and formats/value labels.

The Chi-Square Test of Independence determines whether there is an association between categorical variables (i.e., whether the variables are independent or related). It is a nonparametric test.

This test is also known as:

• Chi-Square Test of Association.

This test utilizes a contingency table to analyze the data. A contingency table (also known as a cross-tabulation , crosstab , or two-way table ) is an arrangement in which data is classified according to two categorical variables. The categories for one variable appear in the rows, and the categories for the other variable appear in columns. Each variable must have two or more categories. Each cell reflects the total count of cases for a specific pair of categories.

There are several tests that go by the name "chi-square test" in addition to the Chi-Square Test of Independence. Look for context clues in the data and research question to make sure what form of the chi-square test is being used.

Common Uses

The Chi-Square Test of Independence is commonly used to test the following:

• Statistical independence or association between two categorical variables.

The Chi-Square Test of Independence can only compare categorical variables. It cannot make comparisons between continuous variables or between categorical and continuous variables. Additionally, the Chi-Square Test of Independence only assesses associations between categorical variables, and can not provide any inferences about causation.

If your categorical variables represent "pre-test" and "post-test" observations, then the chi-square test of independence is not appropriate . This is because the assumption of the independence of observations is violated. In this situation, McNemar's Test is appropriate.

Data Requirements

Your data must meet the following requirements:

• Two categorical variables.
• Two or more categories (groups) for each variable.
• There is no relationship between the subjects in each group.
• The categorical variables are not "paired" in any way (e.g. pre-test/post-test observations).
• Expected frequencies for each cell are at least 1.
• Expected frequencies should be at least 5 for the majority (80%) of the cells.

The null hypothesis ( H 0 ) and alternative hypothesis ( H 1 ) of the Chi-Square Test of Independence can be expressed in two different but equivalent ways:

H 0 : "[ Variable 1 ] is independent of [ Variable 2 ]" H 1 : "[ Variable 1 ] is not independent of [ Variable 2 ]"

H 0 : "[ Variable 1 ] is not associated with [ Variable 2 ]" H 1 :  "[ Variable 1 ] is associated with [ Variable 2 ]"

Test Statistic

The test statistic for the Chi-Square Test of Independence is denoted Χ 2 , and is computed as:

$$ \chi^{2} = \sum_{i=1}^{R}{\sum_{j=1}^{C}{\frac{(o_{ij} - e_{ij})^{2}}{e_{ij}}}} $$

\(o_{ij}\) is the observed cell count in the i th row and j th column of the table

\(e_{ij}\) is the expected cell count in the i th row and j th column of the table, computed as

$$ e_{ij} = \frac{\mathrm{ \textrm{row } \mathit{i}} \textrm{ total} * \mathrm{\textrm{col } \mathit{j}} \textrm{ total}}{\textrm{grand total}} $$

The quantity ( o ij - e ij ) is sometimes referred to as the residual of cell ( i , j ), denoted \(r_{ij}\).

The calculated Χ 2 value is then compared to the critical value from the Χ 2 distribution table with degrees of freedom df = ( R - 1)( C - 1) and chosen confidence level. If the calculated Χ 2 value > critical Χ 2 value, then we reject the null hypothesis.

Data Set-Up

There are two different ways in which your data may be set up initially. The format of the data will determine how to proceed with running the Chi-Square Test of Independence. At minimum, your data should include two categorical variables (represented in columns) that will be used in the analysis. The categorical variables must include at least two groups. Your data may be formatted in either of the following ways:

If you have the raw data (each row is a subject):

• Cases represent subjects, and each subject appears once in the dataset. That is, each row represents an observation from a unique subject.
• The dataset contains at least two nominal categorical variables (string or numeric). The categorical variables used in the test must have two or more categories.

If you have frequencies (each row is a combination of factors):

An example of using the chi-square test for this type of data can be found in the Weighting Cases tutorial .

• Each row in the dataset represents a distinct combination of the categories.
• The value in the "frequency" column for a given row is the number of unique subjects with that combination of categories.
• You should have three variables: one representing each category, and a third representing the number of occurrences of that particular combination of factors.
• Before running the test, you must activate Weight Cases, and set the frequency variable as the weight.

Run a Chi-Square Test of Independence

In SPSS, the Chi-Square Test of Independence is an option within the Crosstabs procedure. Recall that the Crosstabs procedure creates a contingency table or two-way table , which summarizes the distribution of two categorical variables.

To create a crosstab and perform a chi-square test of independence, click  Analyze > Descriptive Statistics > Crosstabs .

A Row(s): One or more variables to use in the rows of the crosstab(s). You must enter at least one Row variable.

B Column(s): One or more variables to use in the columns of the crosstab(s). You must enter at least one Column variable.

Also note that if you specify one row variable and two or more column variables, SPSS will print crosstabs for each pairing of the row variable with the column variables. The same is true if you have one column variable and two or more row variables, or if you have multiple row and column variables. A chi-square test will be produced for each table. Additionally, if you include a layer variable, chi-square tests will be run for each pair of row and column variables within each level of the layer variable.

C Layer: An optional "stratification" variable. If you have turned on the chi-square test results and have specified a layer variable, SPSS will subset the data with respect to the categories of the layer variable, then run chi-square tests between the row and column variables. (This is not equivalent to testing for a three-way association, or testing for an association between the row and column variable after controlling for the layer variable.)

D Statistics: Opens the Crosstabs: Statistics window, which contains fifteen different inferential statistics for comparing categorical variables.

To run the Chi-Square Test of Independence, make sure that the Chi-square box is checked.

E Cells: Opens the Crosstabs: Cell Display window, which controls which output is displayed in each cell of the crosstab. (Note: in a crosstab, the cells are the inner sections of the table. They show the number of observations for a given combination of the row and column categories.) There are three options in this window that are useful (but optional) when performing a Chi-Square Test of Independence:

1 Observed : The actual number of observations for a given cell. This option is enabled by default.

2 Expected : The expected number of observations for that cell (see the test statistic formula).

3 Unstandardized Residuals : The "residual" value, computed as observed minus expected.

F Format: Opens the Crosstabs: Table Format window, which specifies how the rows of the table are sorted.

Example: Chi-square Test for 3x2 Table

Problem statement.

In the sample dataset, respondents were asked their gender and whether or not they were a cigarette smoker. There were three answer choices: Nonsmoker, Past smoker, and Current smoker. Suppose we want to test for an association between smoking behavior (nonsmoker, current smoker, or past smoker) and gender (male or female) using a Chi-Square Test of Independence (we'll use α = 0.05).

Before the Test

Before we test for "association", it is helpful to understand what an "association" and a "lack of association" between two categorical variables looks like. One way to visualize this is using clustered bar charts. Let's look at the clustered bar chart produced by the Crosstabs procedure.

This is the chart that is produced if you use Smoking as the row variable and Gender as the column variable (running the syntax later in this example):

The "clusters" in a clustered bar chart are determined by the row variable (in this case, the smoking categories). The color of the bars is determined by the column variable (in this case, gender). The height of each bar represents the total number of observations in that particular combination of categories.

This type of chart emphasizes the differences within the categories of the row variable. Notice how within each smoking category, the heights of the bars (i.e., the number of males and females) are very similar. That is, there are an approximately equal number of male and female nonsmokers; approximately equal number of male and female past smokers; approximately equal number of male and female current smokers. If there were an association between gender and smoking, we would expect these counts to differ between groups in some way.

Running the Test

• Open the Crosstabs dialog ( Analyze > Descriptive Statistics > Crosstabs ).
• Select Smoking as the row variable, and Gender as the column variable.
• Click Statistics . Check Chi-square , then click Continue .
• (Optional) Check the box for Display clustered bar charts .

The first table is the Case Processing summary, which tells us the number of valid cases used for analysis. Only cases with nonmissing values for both smoking behavior and gender can be used in the test.

The next tables are the crosstabulation and chi-square test results.

The key result in the Chi-Square Tests table is the Pearson Chi-Square.

• The value of the test statistic is 3.171.
• The footnote for this statistic pertains to the expected cell count assumption (i.e., expected cell counts are all greater than 5): no cells had an expected count less than 5, so this assumption was met.
• Because the test statistic is based on a 3x2 crosstabulation table, the degrees of freedom (df) for the test statistic is $$ df = (R - 1)*(C - 1) = (3 - 1)*(2 - 1) = 2*1 = 2 $$.
• The corresponding p-value of the test statistic is p = 0.205.

Decision and Conclusions

Since the p-value is greater than our chosen significance level ( α = 0.05), we do not reject the null hypothesis. Rather, we conclude that there is not enough evidence to suggest an association between gender and smoking.

Based on the results, we can state the following:

• No association was found between gender and smoking behavior ( Χ 2 (2)> = 3.171, p = 0.205).

Example: Chi-square Test for 2x2 Table

Let's continue the row and column percentage example from the Crosstabs tutorial, which described the relationship between the variables RankUpperUnder (upperclassman/underclassman) and LivesOnCampus (lives on campus/lives off-campus). Recall that the column percentages of the crosstab appeared to indicate that upperclassmen were less likely than underclassmen to live on campus:

• The proportion of underclassmen who live off campus is 34.8%, or 79/227.
• The proportion of underclassmen who live on campus is 65.2%, or 148/227.
• The proportion of upperclassmen who live off campus is 94.4%, or 152/161.
• The proportion of upperclassmen who live on campus is 5.6%, or 9/161.

Suppose that we want to test the association between class rank and living on campus using a Chi-Square Test of Independence (using α = 0.05).

The clustered bar chart from the Crosstabs procedure can act as a complement to the column percentages above. Let's look at the chart produced by the Crosstabs procedure for this example:

The height of each bar represents the total number of observations in that particular combination of categories. The "clusters" are formed by the row variable (in this case, class rank). This type of chart emphasizes the differences within the underclassmen and upperclassmen groups. Here, the differences in number of students living on campus versus living off-campus is much starker within the class rank groups.

• Select RankUpperUnder as the row variable, and LiveOnCampus as the column variable.
• (Optional) Click Cells . Under Counts, check the boxes for Observed and Expected , and under Residuals, click Unstandardized . Then click Continue .

The first table is the Case Processing summary, which tells us the number of valid cases used for analysis. Only cases with nonmissing values for both class rank and living on campus can be used in the test.

The next table is the crosstabulation. If you elected to check off the boxes for Observed Count, Expected Count, and Unstandardized Residuals, you should see the following table:

With the Expected Count values shown, we can confirm that all cells have an expected value greater than 5.

These numbers can be plugged into the chi-square test statistic formula:

$$ \chi^{2} = \sum_{i=1}^{R}{\sum_{j=1}^{C}{\frac{(o_{ij} - e_{ij})^{2}}{e_{ij}}}} = \frac{(-56.147)^{2}}{135.147} + \frac{(56.147)^{2}}{91.853} + \frac{(56.147)^{2}}{95.853} + \frac{(-56.147)^{2}}{65.147} = 138.926 $$

We can confirm this computation with the results in the Chi-Square Tests table:

The row of interest here is Pearson Chi-Square and its footnote.

• The value of the test statistic is 138.926.
• Because the crosstabulation is a 2x2 table, the degrees of freedom (df) for the test statistic is $$ df = (R - 1)*(C - 1) = (2 - 1)*(2 - 1) = 1 $$.
• The corresponding p-value of the test statistic is so small that it is cut off from display. Instead of writing "p = 0.000", we instead write the mathematically correct statement p < 0.001.

Since the p-value is less than our chosen significance level α = 0.05, we can reject the null hypothesis, and conclude that there is an association between class rank and whether or not students live on-campus.

• There was a significant association between class rank and living on campus ( Χ 2 (1) = 138.9, p < .001).
• << Previous: Analyzing Data
• Next: Pearson Correlation >>
• Last Updated: Apr 10, 2024 4:50 PM
• URL: https://libguides.library.kent.edu/SPSS

Street Address

Mailing address, quick links.

• How Are We Doing?
• Student Jobs

Information

• Accessibility
• Emergency Information
• For Our Alumni
• For the Media
• Jobs & Employment
• Life at KSU
• Privacy Statement
• Technology Support
• Website Feedback

Tutorial: Pearson's Chi-square Test for Independence

Ling 300, fall 2008.

Sociology 3112

Department of sociology, main navigation, the chi-square test for independence, learning objectives.

• Understand the characteristics of the chi-square distribution
• Carry out the chi-square test and interpret its results
• Understand the limitations of the chi-square test

Chi-Square Distribution: a family asymmetrical, positively skewed distributions, the exact shape of which is determined by their respective degrees of freedom Observed Frequencies: the cell frequencies actually observed in a bivariate table Expected Frequencies: The cell frequencies that one might expect to see in a bivariate table if the two variables were statistically independent

The primary use of the chi-square test is to examine whether two variables are independent or not. What does it mean to be independent, in this sense? It means that the two factors are not related. Typically in social science research, we're interested in finding factors that are dependent upon each other—education and income, occupation and prestige, age and voting behavior. By ruling out independence of the two variables, the chi-square can be used to assess whether two variables are, in fact, dependent or not. More generally, we say that one variable is "not correlated with" or "independent of" the other if an increase in one variable is not associated with an increase in the another. If two variables are correlated, their values tend to move together, either in the same or in the opposite direction. Chi-square examines a special kind of correlation: that between two nominal variables.

The Chi-Square Distribution

The chi-square distribution, like the t distribution, is actually a series of distributions, the exact shape of which varies according to their degrees of freedom. Unlike the t distribution, however, the chi-square distribution is asymmetrical, positively skewed and never approaches normality. The graph below illustrates how the shape of the chi-square distribution changes as the degrees of freedom (k) increase:

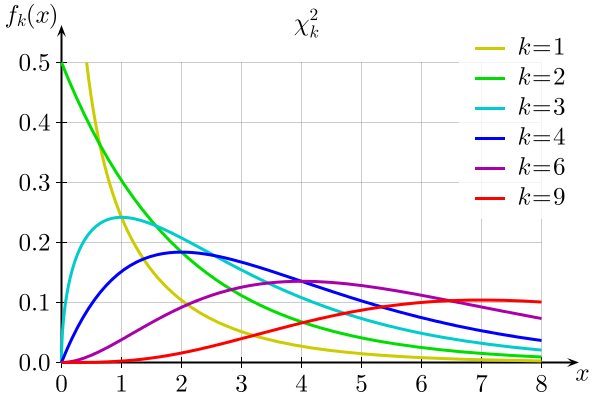
The Chi-Square Test

Earlier in the semester, you familiarized yourself with the five steps of hypothesis testing: (1) making assumptions (2) stating the null and research hypotheses and choosing an alpha level (3) selecting a sampling distribution and determining the test statistic that corresponds with the chosen alpha level (4) calculating the test statistic and (5) interpreting the results. Like the t tests we discussed previously, the chi-square test begins with a handful of assumptions, a pair of hypotheses, a sampling distribution and an alpha level and ends with a conclusion obtained via comparison of an obtained statistic with a critical statistic. The assumptions associated with the chi-square test are fairly straightforward: the data at hand must have been randomly selected (to minimize potential biases) and the variables in question must be nominal or ordinal (there are other methods to test the statistical independence of interval/ratio variables; these methods will be discussed in subsequent chapters). Regarding the hypotheses to be tested, all chi-square tests have the same general null and research hypotheses. The null hypothesis states that there is no relationship between the two variables, while the research hypothesis states that there is a relationship between the two variables. The test statistic follows a chi-square distribution, and the conclusion depends on whether or not our obtained statistic is greater that the critical statistic at our chosen alpha level .

In the following example, we'll use a chi-square test to determine whether there is a relationship between gender and getting in trouble at school (both nominal variables). Below is the table documenting the raw scores of boys and girls and their respective behavior issues (or lack thereof):

Gender and Getting in Trouble at School

To examine statistically whether boys got in trouble in school more often, we need to frame the question in terms of hypotheses. The null hypothesis is that the two variables are independent (i.e. no relationship or correlation) and the research hypothesis is that the two variables are related. In this case, the specific hypotheses are:

H0: There is no relationship between gender and getting in trouble at school H1: There is a relationship between gender and getting in trouble at school

As is customary in the social sciences, we'll set our alpha level at 0.05

Next we need to calculate the expected frequency for each cell. These values represent what we would expect to see if there really were no relationship between the two variables. We calculate the expected frequency for each cell by multiplying the row total by the column total and dividing by the total number of observations. To get the expected count for the upper right cell, we would multiply the row total (117) by the column total (83) and divide by the total number of observations (237). (83 x 117)/237 = 40.97. If the two variables were independent, we would expect 40.97 boys to get in trouble. Or, to put it another way, if there were no relationship between the two variables, we would expect to see the number of students who got in trouble be evenly distributed across both genders.

We do the same thing for the other three cells and end up with the following expected counts (in parentheses next to each raw score):

With these sets of figures, we calculate the chi-square statistic as follows:

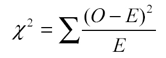
For each cell, we square the difference between the observed frequency and the expected frequency (observed frequency – expected frequency) and divide that number by the expected frequency. Then we add all of the terms (there will be four, one for each cell) together, like so:

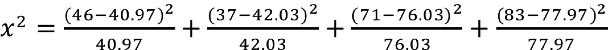
After we've crunched all those numbers, we end up with an obtained statistic of 1.87. ( Please note: a chi-square statistic can't be negative because nominal variables don't have directionality. If your obtained statistic turns out to be negative, you might want to check your math.) But before we can come to a conclusion, we need to find our critical statistic, which entails finding our degrees of freedom. In this case, the number of degrees of freedom is equal to the number of columns in the table minus one multiplied by the number of rows in the table minus one, or (r-1)(c-1). In our case, we have (2-1)(2-1), or one degree of freedom.

Finally, we compare our obtained statistic to our critical statistic found on the chi-square table posted in the "Files" section on Canvas. We also need to reference our alpha, which we set at .05. As you can see, the critical statistic for an alpha level of 0.05 and one degree of freedom is 3.841, which is larger than our obtained statistic of 1.87. Because the critical statistic is greater than our obtained statistic, we can't reject our null hypothesis.

The Limitations of the Chi-Square Test

There are two limitations to the chi-square test about which you should be aware. First, the chi-square test is very sensitive to sample size. With a large enough sample, even trivial relationships can appear to be statistically significant. When using the chi-square test, you should keep in mind that "statistically significant" doesn't necessarily mean "meaningful." Second, remember that the chi-square can only tell us whether two variables are related to one another. It does not necessarily imply that one variable has any causal effect on the other. In order to establish causality, a more detailed analysis would be required.

Main Points

• The chi-square distribution is actually a series of distributions that vary in shape according to their degrees of freedom.
• The chi-square test is a hypothesis test designed to test for a statistically significant relationship between nominal and ordinal variables organized in a bivariate table. In other words, it tells us whether two variables are independent of one another.
• The obtained chi-square statistic essentially summarizes the difference between the frequencies actually observed in a bivariate table and the frequencies we would expect to see if there were no relationship between the two variables.
• The chi-square test is sensitive to sample size.
• The chi-square test cannot establish a causal relationship between two variables.

Carrying out the Chi-Square Test in SPSS

To perform a chi square test with SPSS, click "Analyze," then "Descriptive Statistics," and then "Crosstabs." As was the case in the last chapter, the independent variable should be placed in the "Columns" box, and the dependent variable should be placed in the "Rows" box. Now click on "Statistics" and check the box next to "Chi-Square." This test will provide evidence either in favor of or against the statistical independence of two variables, but it won't give you any information about the strength or direction of the relationship.

After looking at the output, some of you are probably wondering why SPSS provides you with a two-tailed p-value when chi-square is always a one-tailed test. In all honesty, I don't know the answer to that question. However, all is not lost. Because two-tailed tests are always more conservative than one-tailed tests (i.e., it's harder to reject your null hypothesis with a two-tailed test than it is with a one-tailed test), a statistically significant result under a two-tailed assumption would also be significant under a one-tailed assumption. If you're highly motivated, you can compare the obtained statistic from your output to the critical statistic found on a chi-square chart. Here's a video walkthrough with a slightly more detailed explanation:

• Using the World Values Survey data, run a chi-square test to determine whether there is a relationship between sex ("SEX") and marital status ("MARITAL"). Report the obtained statistic and the p-value from your output. What is your conclusion?
• Using the ADD Health data, run a chi-square test to determine whether there is a relationship between the respondent's gender ("GENDER") and his or her grade in math ("MATH"). Again, report the obtained statistic and the p-value from your output. What is your conclusion?

Chi square test

A chi-square test is a type of statistical hypothesis test that is used for populations that exhibit a chi-square distribution.

There are a number of different types of chi-square tests, the most commonly used of which is the Pearson's chi-square test. The Pearson's chi-square test is typically used for data that is categorical (types of data that may be divided into groups, e.g. age, race, sex, age), and may be used to test three types of comparison: independence, goodness of fit, and homogeneity. Most commonly, it is used to test for independence and goodness of fit. These are the two types of chi-square test discussed on this page. The procedure for conducting both tests follows the same general procedure, but certain aspects differ, such as the calculation of the test statistic and degrees of freedom, the conditions under which each test is used, the form of their null and alternative hypotheses, and the conditions for rejection of the null hypothesis. The general procedure for a chi-square test is as follows:

• State the null and alternative hypotheses.
• Select the significance level, α.
• Calculate the test statistic (the chi-square statistic, χ 2 , for the observed value).
• Determine the critical region for the selected level of significance and the appropriate degrees of freedom.
• Compare the test statistic to the critical value, and reject or fail to reject the null hypothesis based on the result.

Chi-square goodness of fit test

The chi-square goodness of fit test is used to test how well a sample of data fits some theoretical distribution. In other words, it can be used to help determine how well a model actually reflects the data based on how close observed values are to what we would expect of values for a normally distributed model.

To conduct a chi-square goodness of fit test, it is necessary to first state the null and alternative hypotheses, which take the following form for this type of test:

Like other hypothesis tests, the significance level of the test is selected by the researcher. The chi-square statistic is then calculated using a sample taken from the relevant population. The sample is grouped into categories such that each category contains a certain number of observed values, referred to as the frequency for the category. As a rule of thumb, the expected frequency for a category should be at least 5 for the chi-square approximation to valid; it is not valid for small samples. The formula for the chi-square statistic, χ 2 , is shown below

where O i is the observed frequency for category i, E i is the observed frequency for category i, and n is the number of categories.

Once the test statistic has been calculated, the critical value for the selected level of significance can be determined using a chi-square table given that the degrees of freedom is n - 1. The value of the test statistic is then compared to the critical value, and if it is greater than the critical value, the null hypothesis is rejected in favor of the alternative hypothesis; if the value of the test statistic is less than the critical value, we fail to reject the null hypothesis.

Jennifer wants to know if a six-sided die she just purchased is fair (each side has an equal probability of occurring). She rolls the die 60 times and records the following outcomes:

Use a chi-square goodness of fit test with a significance level of α = 0.05 to test the fairness of the die.

The null and alternative hypotheses can be stated as follows:

Since there is a 1/6 probability of any one of the numbers occurring on any given roll, and Jennifer rolled the die 60 times, she can expect to roll each face 10 times. Given the expected frequency, χ 2 can then be calculated as follows:

Thus, χ 2 = 10. The degrees of freedom can be found as n - 1, or 6 - 1 = 5. Thus df = 5. Referencing an upper-tail chi-square table for a significance level of 0.05 and df = 5, the critical value, is 11.07. Since the test statistic is less than the critical value, we fail to reject the null hypothesis. Thus, there is insufficient evidence to suggest that the die is unfair at a significance level of 0.05. This is depicted in the figure below.

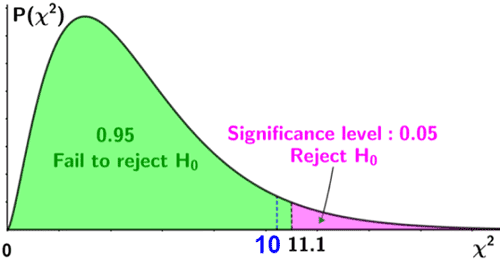
Chi-square test of independence

The chi-square test of independence is used to help determine whether the differences between the observed and expected values of certain variables of interest indicate a statistically significant association between the variables, or if the differences can be simply attributed to chance; in other words, it is used to determine whether the value of one categorical variable depends on that of the other variable(s). In this type of hypothesis test, the null and alternative hypotheses take the following form:

Though the chi-square statistic is defined similarly for both the test of independence and goodness of fit, the expected value for the test of independence is calculated differently, since it involves two variables rather than one. Let X and Y be the two variables being tested such that X has i categories and Y has j categories. The number of combinations of the categories for X and Y forms a contingency table that has i rows and j columns. Since we are assuming that the null hypothesis is true, and X and Y are independent variables, the expected value can be computed as

where n i is the total of the observed frequencies in the i th row, n j is the total of the observed frequencies in the j th column, and n is the sample size. χ 2 is then defined as

where O ij is the observed value in row i and column j , E ij is the expected value in row i and column j , p is the number of rows, and q is the number of columns in the contingency table. Also, note that p represents the number of categories for one of the variables while q represents the number of categories for the other variable.

For a chi-square test of independence, the degrees of freedom can be determined as:

df = (p - 1)(q - 1)

Once df is known, the critical value and critical region can be determined for the selected significance level, and we can either reject or fail to reject the null hypothesis based on the results. Specifically:

• For an upper-tailed one-sided test, use a table of upper-tail critical values. If the test statistic is greater than the value in the column of the table corresponding to (1 - α), reject the null hypothesis.
• For a lower-tailed one-sided test, use a table of lower-tail critical values. If the test statistic is less than the value in the column of the table corresponding to α, reject the null hypothesis.
• Upper tail: if the test statistic is greater than the value in the column corresponding to (1 - α/2), reject the null hypothesis.
• Lower tail: if the test statistic is less than the value in the column corresponding to α/2, reject the null hypothesis.

The figure below depicts the above criteria for rejection of the null hypothesis.

A survey of 500 people is conducted to determine whether there is a relationship between a person's sex and their favorite color. A choice of three colors (blue, red, green) was provided, and the results of the survey are shown in the contingency table below:

Conduct a chi-square test of independence to test whether there is a relationship between sex and color preference at a significance level of α = 0.05.

E ij is computed for each row and column as follows:

The chi-square statistic is then computed as:

The degrees of freedom is computed as:

df = (2 - 1)(3 - 1) = 2

Thus, using a chi-square table, the critical value for α = 0.05 and df = 2 is 5.99. Since the test statistic, χ 2 = 13.5, is greater than the critical value, it lies in the critical region, so we reject the null hypothesis in favor of the alternative hypothesis at a significance level of 0.05.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 12.

• Introduction to the chi-square test for homogeneity

Chi-square test for association (independence)

• Expected counts in chi-squared tests with two-way tables
• Test statistic and P-value in chi-square tests with two-way tables
• Making conclusions in chi-square tests for two-way tables

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

LEARN STATISTICS EASILY

Learn Data Analysis Now!

Understanding the Null Hypothesis in Chi-Square

The null hypothesis in chi square testing suggests no significant difference between a study’s observed and expected frequencies. It assumes any observed difference is due to chance and not because of a meaningful statistical relationship.

Introduction

The chi-square test is a valuable tool in statistical analysis. It’s a non-parametric test applied when the data are qualitative or categorical. This test helps to establish whether there is a significant association between 2 categorical variables in a sample population.

Central to any chi-square test is the concept of the null hypothesis. In the context of chi-square, the null hypothesis assumes no significant difference exists between the categories’ observed and expected frequencies. Any difference seen is likely due to chance or random error rather than a meaningful statistical difference.

• The chi-square null hypothesis assumes no significant difference between observed and expected frequencies.
• Failing to reject the null hypothesis doesn’t prove it true, only that data lacks strong evidence against it.
• A p-value < the significance level indicates a significant association between variables.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Understanding the Concept of Null Hypothesis in Chi Square

The null hypothesis in chi-square tests is essentially a statement of no effect or no relationship. When it comes to categorical data, it indicates that the distribution of categories for one variable is not affected by the distribution of categories of the other variable.

For example, if we compare the preference for different types of fruit among men and women, the null hypothesis would state that the preference is independent of gender. The alternative hypothesis, on the other hand, would suggest a dependency between the two.

Steps to Formulate the Null Hypothesis in Chi-Square Tests

Formulating the null hypothesis is a critical step in any chi-square test. First, identify the variables being tested. Then, once the variables are determined, the null hypothesis can be formulated to state no association between them.

Next, collect your data. This data must be frequencies or counts of categories, not percentages or averages. Once the data is collected, you can calculate the expected frequency for each category under the null hypothesis.

Finally, use the chi-square formula to calculate the chi-square statistic. This will help determine whether to reject or fail to reject the null hypothesis.

Practical Example and Case Study

Consider a study evaluating whether smoking status is independent of a lung cancer diagnosis. The null hypothesis would state that smoking status (smoker or non-smoker) is independent of cancer diagnosis (yes or no).

If we find a p-value less than our significance level (typically 0.05) after conducting the chi-square test, we would reject the null hypothesis and conclude that smoking status is not independent of lung cancer diagnosis, suggesting a significant association between the two.

Observed Table

Expected table, common misunderstandings and pitfalls.

One common misunderstanding is the interpretation of failing to reject the null hypothesis. It’s important to remember that failing to reject the null does not prove it true. Instead, it merely suggests that our data do not provide strong enough evidence against it.

Another pitfall is applying the chi-square test to inappropriate data. The chi-square test requires categorical or nominal data. Applying it to ordinal or continuous data without proper binning or categorization can lead to incorrect results.

The null hypothesis in chi-square testing is a powerful tool in statistical analysis. It provides a means to differentiate between observed variations due to random chance versus those that may signify a significant effect or relationship. As we continue to generate more data in various fields, the importance of understanding and correctly applying chi-square tests and the concept of the null hypothesis grows.

Recommended Articles

Interested in diving deeper into statistics? Explore our range of statistical analysis and data science articles to broaden your understanding. Visit our blog now!

• Simple Null Hypothesis – an overview (External Link)
• Chi-Square Calculator: Enhance Your Data Analysis Skills
• Effect Size for Chi-Square Tests: Unveiling its Significance
• What is the Difference Between the T-Test vs. Chi-Square Test?
• Understanding the Assumptions for Chi-Square Test of Independence

How to Report Chi-Square Test Results in APA Style: A Step-By-Step Guide

Frequently asked questions (faqs).

It’s a statistical test used to determine if there’s a significant association between two categorical variables.

The null hypothesis suggests no significant difference between observed and expected frequencies exists. The alternative hypothesis suggests a significant difference.

No, we never “accept” the null hypothesis. We only fail to reject it if the data doesn’t provide strong evidence against it.

Rejecting the null hypothesis implies a significant difference between observed and expected frequencies, suggesting an association between variables.

Chi-Square tests are appropriate for categorical or nominal data.

The significance level, often 0.05, is the probability threshold below which the null hypothesis can be rejected.

A p-value < the significance level indicates a significant association between variables, leading to rejecting the null hypothesis.

Using the Chi-Square test for improper data, like ordinal or continuous data, without proper categorization can lead to incorrect results.

Identify the variables, state their independence, collect data, calculate expected frequencies, and apply the Chi-Square formula.

Understanding the null hypothesis is essential for correctly interpreting and applying Chi-Square tests, helping to make informed decisions based on data.

Similar Posts

Is PSPP A Free Alternative To SPSS?

Explore PSPP, a free alternative to SPSS, offering similar functionality and user interface for data analysis.

RM ANOVA: The Definitive Guide to Understanding Within-Subject Variability

Discover the essence of RM ANOVA in our comprehensive guide, mastering within-subject variability analysis for impactful research insights.

Statistics vs Parameters: A Comprehensive FAQ Guide

Discover the differences between statistics and parameters in data analysis, their applications, and how to effectively use and communicate these critical concepts.

This is a concise guide on how to report Chi-Square Test results in APA style, including significance, p-value, and effect size.

Create Great Graphs Easily (+Bonus)

Master the art of graph creation using iNZight, a free software offering various chart types and inferential analysis for compelling data presentations.

A Comprehensive Guide to How Standard Deviation is Calculated

Unlock the power of data analysis by learning how standard deviation is calculated. Enhance your statistical skills with our guide.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

R news and tutorials contributed by hundreds of R bloggers

Estimating chi-square distribution parameters using r.

Posted on April 14, 2024 by Steven P. Sanderson II, MPH in R bloggers | 0 Comments

Introduction

In the world of statistics and data analysis, understanding and accurately estimating the parameters of probability distributions is crucial. One such distribution is the chi-square distribution, often encountered in various statistical analyses. In this blog post, we’ll dive into how we can estimate the degrees of freedom (“df”) and the non-centrality parameter (“ncp”) of a chi-square distribution using R programming language.

The Chi-Square Distribution

The chi-square distribution is a continuous probability distribution that arises in the context of hypothesis testing and confidence interval estimation. It is commonly used in goodness-of-fit tests, tests of independence, and tests of homogeneity.

The distribution has two main parameters: – Degrees of Freedom (df) : This parameter determines the shape of the chi-square distribution. It represents the number of independent variables in a statistical test. – Non-Centrality Parameter (ncp) : This parameter determines the deviation of the distribution from a null hypothesis. It’s particularly relevant in non-central chi-square distributions.

The Goal: Estimating Parameters

Our goal is to create a function within the TidyDensity package that can estimate the df and ncp parameters of a chi-square distribution based on a vector of observed data. Let’s walk through the steps involved in achieving this.

Working Example

Setting the stage: libraries and data.

First, we load the necessary libraries: tidyverse for data manipulation and bbmle for maximum likelihood estimation. We then generate a grid of parameters (degrees of freedom and non-centrality parameter) and sample sizes to create a diverse set of chi-square distributed data.

Function Exploration: Unveiling the Estimation Process

The core of our exploration lies in several functions designed to estimate the chi-square parameters:

dof / k Functions: These functions focus on estimating the degrees of freedom (df) using different approaches:

• mean_x : Calculates the mean of the data.
• mean_minus_1 : Subtracts 1 from the mean.
• var_div_2 : Divides the variance of the data by 2.
• length_minus_1 : Subtracts 1 from the length of the data.

ncp Functions: These functions aim to estimate the non-centrality parameter (ncp) using various methods:

• mean_minus_mean_minus_1 : A seemingly trivial calculation that serves as a baseline.
• ie_mean_minus_var_div_2 : Subtracts half the variance from the mean, ensuring the result is non-negative.
• ie_optim : Utilizes optimization techniques to find the ncp that maximizes the likelihood of observing the data.
• estimate_chisq_params : This is the main function that employs maximum likelihood estimation (MLE) via the bbmle package to estimate both df and ncp simultaneously. It defines a negative log-likelihood function based on the chi-square distribution and uses mle2 to find the parameter values that minimize this function.

Simulating and Evaluating: Putting the Functions to the Test

To assess the performance of our functions, we simulate chi-square data using the parameter grid and apply each function to estimate the parameters. We then compare these estimates to the true values and visualize the results using boxplots.

Visual Insights: Assessing Estimation Accuracy

The boxplots reveal interesting insights:

df Estimation:

• mean_x - 1 and var(x) / 2 show potential as df estimators but exhibit bias depending on the true df value.
• length(x) - 1 performs poorly, consistently underestimating df.
• The MLE approach from estimate_chisq_params demonstrates the most accurate and unbiased estimates across different df values.

ncp Estimation:

• The simple methods ( mean(x) - mean(x) - 1 and mean(x) - var(x) / 2 ) show substantial bias and variability.
• The optimization-based method ( optim ) performs better but still exhibits some bias.
• The MLE approach again emerges as the most reliable option, providing accurate and unbiased estimates across various ncp values.

Conclusion: The Power of Maximum Likelihood

Our exploration highlights the effectiveness of MLE in estimating the parameters of a chi-square distribution. The estimate_chisq_params function, utilizing the bbmle package, provides a robust and accurate solution for this task. This function will be a valuable addition to the TidyDensity package, empowering users to delve deeper into the analysis of chi-square distributed data.

Stay tuned for further developments and exciting additions to the TidyDensity package!

Copyright © 2024 | MH Corporate basic by MH Themes

Never miss an update! Subscribe to R-bloggers to receive e-mails with the latest R posts. (You will not see this message again.)