Common Core Algebra I Math (Worksheets, Homework, Lesson Plans)
Related Topics: Common Core Math Resources, Lesson Plans & Worksheets for all grades Common Core Math Video Lessons, Math Worksheets and Games for Algebra Common Core Math Video Lessons, Math Worksheets and Games for all grades
Looking for video lessons that will help you in your Common Core Algebra I math classwork or homework? Looking for Common Core Math Worksheets and Lesson Plans that will help you prepare lessons for Algebra I students?
The following lesson plans and worksheets are from the New York State Education Department Common Core-aligned educational resources. Eureka/EngageNY Math Algebra I Worksheets.
These Lesson Plans and Worksheets are divided into five modules.

Algebra I Homework, Lesson Plans and Worksheets

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
3.1 Functions and Function Notation
Learning objectives.
In this section, you will:
- Determine whether a relation represents a function.
- Find the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions listed in the library of functions.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Determining Whether a Relation Represents a Function
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range . Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.
The domain is { 1 , 2 , 3 , 4 , 5 } . { 1 , 2 , 3 , 4 , 5 } . The range is { 2 , 4 , 6 , 8 , 10 } . { 2 , 4 , 6 , 8 , 10 } .
Note that each value in the domain is also known as an input value, or independent variable , and is often labeled with the lowercase letter x . x . Each value in the range is also known as an output value, or dependent variable , and is often labeled lowercase letter y . y .
A function f f is a relation that assigns a single value in the range to each value in the domain . In other words, no x -values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, { 1 , 2 , 3 , 4 , 5 } , { 1 , 2 , 3 , 4 , 5 } , is paired with exactly one element in the range, { 2 , 4 , 6 , 8 , 10 } . { 2 , 4 , 6 , 8 , 10 } .
Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
Notice that each element in the domain, { even, odd } { even, odd } is not paired with exactly one element in the range, { 1 , 2 , 3 , 4 , 5 } . { 1 , 2 , 3 , 4 , 5 } . For example, the term “odd” corresponds to three values from the range, { 1 , 3 , 5 } { 1 , 3 , 5 } and the term “even” corresponds to two values from the range, { 2 , 4 } . { 2 , 4 } . This violates the definition of a function, so this relation is not a function.
Figure 1 compares relations that are functions and not functions.
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain , and the output values make up the range .
Given a relationship between two quantities, determine whether the relationship is a function.
- Identify the input values.
- Identify the output values.
- If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.
Determining If Menu Price Lists Are Functions
The coffee shop menu, shown below, consists of items and their prices. ⓐ Is price a function of the item? ⓑ Is the item a function of the price?
ⓐ Let’s begin by considering the input as the items on the menu. The output values are then the prices.
Each item on the menu has only one price, so the price is a function of the item. ⓑ Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it. See the image below.
Therefore, the item is a not a function of price.
Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? Table 1 shows a possible rule for assigning grade points.
For any percent grade earned, there is an associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average.
In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.
Table 2 1 lists the five greatest baseball players of all time in order of rank.
- ⓐ Is the rank a function of the player name?
- ⓑ Is the player name a function of the rank?
Using Function Notation
Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions.
To represent “height is a function of age,” we start by identifying the descriptive variables h h for height and a a for age. The letters f , g , f , g , and h h are often used to represent functions just as we use x , y , x , y , and z z to represent numbers and A , B , A , B , and C C to represent sets.
Remember, we can use any letter to name the function; the notation h ( a ) h ( a ) shows us that h h depends on a . a . The value a a must be put into the function h h to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication.
We can also give an algebraic expression as the input to a function. For example f ( a + b ) f ( a + b ) means “first add a and b , and the result is the input for the function f .” The operations must be performed in this order to obtain the correct result.
Function Notation
The notation y = f ( x ) y = f ( x ) defines a function named f . f . This is read as “ y “ y is a function of x . ” x . ” The letter x x represents the input value, or independent variable. The letter y , y , or f ( x ) , f ( x ) , represents the output value, or dependent variable.
Using Function Notation for Days in a Month
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month. Assume that the domain does not include leap years.
The number of days in a month is a function of the name of the month, so if we name the function f , f , we write days = f ( month ) days = f ( month ) or d = f ( m ) . d = f ( m ) . The name of the month is the input to a “rule” that associates a specific number (the output) with each input.
For example, f ( March ) = 31 , f ( March ) = 31 , because March has 31 days. The notation d = f ( m ) d = f ( m ) reminds us that the number of days, d d (the output), is dependent on the name of the month, m m (the input).
Note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.
Interpreting Function Notation
A function N = f ( y ) N = f ( y ) gives the number of police officers, N , N , in a town in year y . y . What does f ( 2005 ) = 300 f ( 2005 ) = 300 represent?
When we read f ( 2005 ) = 300 , f ( 2005 ) = 300 , we see that the input year is 2005. The value for the output, the number of police officers ( N ) , ( N ) , is 300. Remember, N = f ( y ) . N = f ( y ) . The statement f ( 2005 ) = 300 f ( 2005 ) = 300 tells us that in the year 2005 there were 300 police officers in the town.
Use function notation to express the weight of a pig in pounds as a function of its age in days d . d .
Instead of a notation such as y = f ( x ), y = f ( x ), could we use the same symbol for the output as for the function, such as y = y ( x ), y = y ( x ), meaning “ y is a function of x ?”
Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as f , f , which is a rule or procedure, and the output y y we get by applying f f to a particular input x . x . This is why we usually use notation such as y = f ( x ) , P = W ( d ) , y = f ( x ) , P = W ( d ) , and so on.
Representing Functions Using Tables
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases, these values represent all we know about the relationship; other times, the table provides a few select examples from a more complete relationship.
Table 3 lists the input number of each month (January = 1, February = 2, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function f f where D = f ( m ) D = f ( m ) identifies months by an integer rather than by name.
Table 4 defines a function Q = g ( n ) . Q = g ( n ) . Remember, this notation tells us that g g is the name of the function that takes the input n n and gives the output Q . Q .
Table 5 displays the age of children in years and their corresponding heights. This table displays just some of the data available for the heights and ages of children. We can see right away that this table does not represent a function because the same input value, 5 years, has two different output values, 40 in. and 42 in.
Given a table of input and output values, determine whether the table represents a function.
- Identify the input and output values.
- Check to see if each input value is paired with only one output value. If so, the table represents a function.
Identifying Tables that Represent Functions
Which table, Table 6 , Table 7 , or Table 8 , represents a function (if any)?
Table 6 and Table 7 define functions. In both, each input value corresponds to exactly one output value. Table 8 does not define a function because the input value of 5 corresponds to two different output values.
When a table represents a function, corresponding input and output values can also be specified using function notation.
The function represented by Table 6 can be represented by writing
Similarly, the statements
represent the function in Table 7 .
Table 8 cannot be expressed in a similar way because it does not represent a function.
Does Table 9 represent a function?
Finding Input and Output Values of a Function
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the function’s formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Evaluation of Functions in Algebraic Forms
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function f ( x ) = 5 − 3 x 2 f ( x ) = 5 − 3 x 2 can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
Given the formula for a function, evaluate.
- Substitute the input variable in the formula with the value provided.
- Calculate the result.
Evaluating Functions at Specific Values
Evaluate f ( x ) = x 2 + 3 x − 4 f ( x ) = x 2 + 3 x − 4 at:
- ⓒ a + h a + h
- ⓓ Now evaluate f ( a + h ) − f ( a ) h f ( a + h ) − f ( a ) h
Replace the x x in the function with each specified value.
- ⓐ Because the input value is a number, 2, we can use simple algebra to simplify. f ( 2 ) = 2 2 + 3 ( 2 ) − 4 = 4 + 6 − 4 = 6 f ( 2 ) = 2 2 + 3 ( 2 ) − 4 = 4 + 6 − 4 = 6
- ⓑ In this case, the input value is a letter so we cannot simplify the answer any further. f ( a ) = a 2 + 3 a − 4 f ( a ) = a 2 + 3 a − 4
- ⓒ With an input value of a + h , a + h , we must use the distributive property. f ( a + h ) = ( a + h ) 2 + 3 ( a + h ) − 4 = a 2 + 2 a h + h 2 + 3 a + 3 h − 4 f ( a + h ) = ( a + h ) 2 + 3 ( a + h ) − 4 = a 2 + 2 a h + h 2 + 3 a + 3 h − 4
and we know that
Now we combine the results and simplify.
Evaluating Functions
Given the function h ( p ) = p 2 + 2 p , h ( p ) = p 2 + 2 p , evaluate h ( 4 ) . h ( 4 ) .
To evaluate h ( 4 ) , h ( 4 ) , we substitute the value 4 for the input variable p p in the given function.
Therefore, for an input of 4, we have an output of 24.
Given the function g ( m ) = m − 4 , g ( m ) = m − 4 , evaluate g ( 5 ) . g ( 5 ) .
Solving Functions
Given the function h ( p ) = p 2 + 2 p , h ( p ) = p 2 + 2 p , solve for h ( p ) = 3. h ( p ) = 3.
If ( p + 3 ) ( p − 1 ) = 0 , ( p + 3 ) ( p − 1 ) = 0 , either ( p + 3 ) = 0 ( p + 3 ) = 0 or ( p − 1 ) = 0 ( p − 1 ) = 0 (or both of them equal 0). We will set each factor equal to 0 and solve for p p in each case.
This gives us two solutions. The output h ( p ) = 3 h ( p ) = 3 when the input is either p = 1 p = 1 or p = − 3. p = − 3. We can also verify by graphing as in Figure 3 . The graph verifies that h ( 1 ) = h ( − 3 ) = 3 h ( 1 ) = h ( − 3 ) = 3 and h ( 4 ) = 24. h ( 4 ) = 24.
Given the function g ( m ) = m − 4 , g ( m ) = m − 4 , solve g ( m ) = 2. g ( m ) = 2.
Evaluating Functions Expressed in Formulas
Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can define a function in algebraic form. For example, the equation 2 n + 6 p = 12 2 n + 6 p = 12 expresses a functional relationship between n n and p . p . We can rewrite it to decide if p p is a function of n . n .
Given a function in equation form, write its algebraic formula.
- Solve the equation to isolate the output variable on one side of the equal sign, with the other side as an expression that involves only the input variable.
- Use all the usual algebraic methods for solving equations, such as adding or subtracting the same quantity to or from both sides, or multiplying or dividing both sides of the equation by the same quantity.
Finding the Algebraic Form of a Function
Express the relationship 2 n + 6 p = 12 2 n + 6 p = 12 as a function p = f ( n ) , p = f ( n ) , if possible.
To express the relationship in this form, we need to be able to write the relationship where p p is a function of n , n , which means writing it as p = [ expression involving n ] . p = [ expression involving n ] .
Therefore, p p as a function of n n is written as
It is important to note that not every relationship expressed by an equation can also be expressed as a function with a formula.
Expressing the Equation of a Circle as a Function
Does the equation x 2 + y 2 = 1 x 2 + y 2 = 1 represent a function with x x as input and y y as output? If so, express the relationship as a function y = f ( x ) . y = f ( x ) .
First we subtract x 2 x 2 from both sides.
We now try to solve for y y in this equation.
We get two outputs corresponding to the same input, so this relationship cannot be represented as a single function y = f ( x ) . y = f ( x ) .
If x − 8 y 3 = 0 , x − 8 y 3 = 0 , express y y as a function of x . x .
Are there relationships expressed by an equation that do represent a function but which still cannot be represented by an algebraic formula?
Yes, this can happen. For example, given the equation x = y + 2 y , x = y + 2 y , if we want to express y y as a function of x , x , there is no simple algebraic formula involving only x x that equals y . y . However, each x x does determine a unique value for y , y , and there are mathematical procedures by which y y can be found to any desired accuracy. In this case, we say that the equation gives an implicit (implied) rule for y y as a function of x , x , even though the formula cannot be written explicitly.
Evaluating a Function Given in Tabular Form
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppy’s memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours.
The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See Table 10 . 2
At times, evaluating a function in table form may be more useful than using equations.Here let us call the function P . P . The domain of the function is the type of pet and the range is a real number representing the number of hours the pet’s memory span lasts. We can evaluate the function P P at the input value of “goldfish.” We would write P ( goldfish ) = 2160. P ( goldfish ) = 2160. Notice that, to evaluate the function in table form, we identify the input value and the corresponding output value from the pertinent row of the table. The tabular form for function P P seems ideally suited to this function, more so than writing it in paragraph or function form.
Given a function represented by a table, identify specific output and input values.
- Find the given input in the row (or column) of input values.
- Identify the corresponding output value paired with that input value.
- Find the given output values in the row (or column) of output values, noting every time that output value appears.
- Identify the input value(s) corresponding to the given output value.
Evaluating and Solving a Tabular Function
Using Table 11 , ⓐ Evaluate g ( 3 ) . g ( 3 ) . ⓑ Solve g ( n ) = 6. g ( n ) = 6.
ⓐ Evaluating g ( 3 ) g ( 3 ) means determining the output value of the function g g for the input value of n = 3. n = 3. The table output value corresponding to n = 3 n = 3 is 7, so g ( 3 ) = 7. g ( 3 ) = 7. ⓑ Solving g ( n ) = 6 g ( n ) = 6 means identifying the input values, n , n , that produce an output value of 6. The table below shows two solutions: 2 2 and 4. 4.
When we input 2 into the function g , g , our output is 6. When we input 4 into the function g , g , our output is also 6.
Using the table from Evaluating and Solving a Tabular Function above, evaluate g ( 1 ) . g ( 1 ) .
Finding Function Values from a Graph
Evaluating a function using a graph also requires finding the corresponding output value for a given input value, only in this case, we find the output value by looking at the graph. Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).
Reading Function Values from a Graph
Given the graph in Figure 4 ,
ⓐ Evaluate f ( 2 ) . f ( 2 ) . ⓑ Solve f ( x ) = 4. f ( x ) = 4.
ⓐ To evaluate f ( 2 ) , f ( 2 ) , locate the point on the curve where x = 2 , x = 2 , then read the y -coordinate of that point. The point has coordinates ( 2 , 1 ) , ( 2 , 1 ) , so f ( 2 ) = 1. f ( 2 ) = 1. See Figure 5 .
ⓑ To solve f ( x ) = 4, f ( x ) = 4, we find the output value 4 4 on the vertical axis. Moving horizontally along the line y = 4 , y = 4 , we locate two points of the curve with output value 4: 4: ( −1 , 4 ) ( −1 , 4 ) and ( 3 , 4 ) . ( 3 , 4 ) . These points represent the two solutions to f ( x ) = 4: f ( x ) = 4: −1 −1 or 3. 3. This means f ( −1 ) = 4 f ( −1 ) = 4 and f ( 3 ) = 4 , f ( 3 ) = 4 , or when the input is −1 −1 or 3, 3, the output is 4 . 4 . See Figure 6 .
Using Figure 4 , solve f ( x ) = 1. f ( x ) = 1.
Determining Whether a Function is One-to-One
Some functions have a given output value that corresponds to two or more input values. For example, in the stock chart shown in the figure at the beginning of this chapter, the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in Table 12 .
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, let’s look again at the two simple functions sketched in Figure 1 (a) and Figure 1 (b) . The function in part (a) shows a relationship that is not a one-to-one function because inputs q q and r r both give output n . n . The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.
One-to-One Function
A one-to-one function is a function in which each output value corresponds to exactly one input value.
Determining Whether a Relationship Is a One-to-One Function
Is the area of a circle a function of its radius? If yes, is the function one-to-one?
A circle of radius r r has a unique area measure given by A = π r 2 , A = π r 2 , so for any input, r , r , there is only one output, A . A . The area is a function of radius r . r .
If the function is one-to-one, the output value, the area, must correspond to a unique input value, the radius. Any area measure A A is given by the formula A = π r 2 . A = π r 2 . Because areas and radii are positive numbers, there is exactly one solution: A π . A π . So the area of a circle is a one-to-one function of the circle’s radius.
- ⓐ Is a balance a function of the bank account number?
- ⓑ Is a bank account number a function of the balance?
- ⓒ Is a balance a one-to-one function of the bank account number?
Evaluate the following: ⓐ If each percent grade earned in a course translates to one letter grade, is the letter grade a function of the percent grade? ⓑ If so, is the function one-to-one?
Using the Vertical Line Test
As we have seen in some examples above, we can represent a function using a graph. Graphs display a great many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value x x and the output value y , y , and we say y y is a function of x , x , or y = f ( x ) y = f ( x ) when the function is named f . f . The graph of the function is the set of all points ( x , y ) ( x , y ) in the plane that satisfies the equation y = f ( x ) . y = f ( x ) . If the function is defined for only a few input values, then the graph of the function is only a few points, where the x -coordinate of each point is an input value and the y -coordinate of each point is the corresponding output value. For example, the black dots on the graph in Figure 7 tell us that f ( 0 ) = 2 f ( 0 ) = 2 and f ( 6 ) = 1. f ( 6 ) = 1. However, the set of all points ( x , y ) ( x , y ) satisfying y = f ( x ) y = f ( x ) is a curve. The curve shown includes ( 0 , 2 ) ( 0 , 2 ) and ( 6 , 1 ) ( 6 , 1 ) because the curve passes through those points.
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. See Figure 8 .
Given a graph, use the vertical line test to determine if the graph represents a function.
- Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
- If there is any such line, determine that the graph does not represent a function.
Applying the Vertical Line Test
Which of the graphs in Figure 9 represent(s) a function y = f ( x ) ? y = f ( x ) ?
If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in parts (a) and (b) of Figure 9 . From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at most x -values, a vertical line would intersect the graph at more than one point, as shown in Figure 10 .
Does the graph in Figure 11 represent a function?
Using the Horizontal Line Test
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test . Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.
Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, determine that the function is not one-to-one.

Applying the Horizontal Line Test
Consider the functions shown in Figure 9 (a) and Figure 9 (b) . Are either of the functions one-to-one?
The function in Figure 9 (a) is not one-to-one. The horizontal line shown in Figure 12 intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)
The function in Figure 9 (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
Is the graph shown in Figure 9 (c) one-to-one?
Identifying Basic Toolkit Functions
In this text, we will be exploring functions—the shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start with the alphabet. When learning to do arithmetic, we start with numbers. When working with functions, it is similarly helpful to have a base set of building-block elements. We call these our “toolkit functions,” which form a set of basic named functions for which we know the graph, formula, and special properties. Some of these functions are programmed to individual buttons on many calculators. For these definitions we will use x x as the input variable and y = f ( x ) y = f ( x ) as the output variable.
We will see these toolkit functions, combinations of toolkit functions, their graphs, and their transformations frequently throughout this book. It will be very helpful if we can recognize these toolkit functions and their features quickly by name, formula, graph, and basic table properties. The graphs and sample table values are included with each function shown in Table 13 .
Access the following online resources for additional instruction and practice with functions.
- Determine if a Relation is a Function
- Vertical Line Test
- Introduction to Functions
- Vertical Line Test on Graph
- One-to-one Functions
- Graphs as One-to-one Functions
3.1 Section Exercises
What is the difference between a relation and a function?
What is the difference between the input and the output of a function?
Why does the vertical line test tell us whether the graph of a relation represents a function?
How can you determine if a relation is a one-to-one function?
Why does the horizontal line test tell us whether the graph of a function is one-to-one?
For the following exercises, determine whether the relation represents a function.
{ ( a , b ) , ( c , d ) , ( a , c ) } { ( a , b ) , ( c , d ) , ( a , c ) }
{ ( a , b ) , ( b , c ) , ( c , c ) } { ( a , b ) , ( b , c ) , ( c , c ) }
For the following exercises, determine whether the relation represents y y as a function of x . x .
5 x + 2 y = 10 5 x + 2 y = 10
y = x 2 y = x 2
x = y 2 x = y 2
3 x 2 + y = 14 3 x 2 + y = 14
2 x + y 2 = 6 2 x + y 2 = 6
y = − 2 x 2 + 40 x y = − 2 x 2 + 40 x
y = 1 x y = 1 x
x = 3 y + 5 7 y − 1 x = 3 y + 5 7 y − 1
x = 1 − y 2 x = 1 − y 2
y = 3 x + 5 7 x − 1 y = 3 x + 5 7 x − 1
x 2 + y 2 = 9 x 2 + y 2 = 9
2 x y = 1 2 x y = 1
x = y 3 x = y 3
y = x 3 y = x 3
y = 1 − x 2 y = 1 − x 2
x = ± 1 − y x = ± 1 − y
y = ± 1 − x y = ± 1 − x
y 2 = x 2 y 2 = x 2
y 3 = x 2 y 3 = x 2
For the following exercises, evaluate f ( −3 ) , f ( 2 ) , f ( − a ) , − f ( a ) , f ( a + h ) . f ( −3 ) , f ( 2 ) , f ( − a ) , − f ( a ) , f ( a + h ) .
f ( x ) = 2 x − 5 f ( x ) = 2 x − 5
f ( x ) = − 5 x 2 + 2 x − 1 f ( x ) = − 5 x 2 + 2 x − 1
f ( x ) = 2 − x + 5 f ( x ) = 2 − x + 5
f ( x ) = 6 x − 1 5 x + 2 f ( x ) = 6 x − 1 5 x + 2
f ( x ) = | x − 1 | − | x + 1 | f ( x ) = | x − 1 | − | x + 1 |
Given the function g ( x ) = 5 − x 2 , g ( x ) = 5 − x 2 , evaluate g ( x + h ) − g ( x ) h , h ≠ 0. g ( x + h ) − g ( x ) h , h ≠ 0.
Given the function g ( x ) = x 2 + 2 x , g ( x ) = x 2 + 2 x , evaluate g ( x ) − g ( a ) x − a , x ≠ a . g ( x ) − g ( a ) x − a , x ≠ a .
Given the function k ( t ) = 2 t − 1 : k ( t ) = 2 t − 1 :
- ⓐ Evaluate k ( 2 ) . k ( 2 ) .
- ⓑ Solve k ( t ) = 7. k ( t ) = 7.
Given the function f ( x ) = 8 − 3 x : f ( x ) = 8 − 3 x :
- ⓐ Evaluate f ( − 2 ) . f ( − 2 ) .
- ⓑ Solve f ( x ) = − 1. f ( x ) = − 1.
Given the function p ( c ) = c 2 + c : p ( c ) = c 2 + c :
- ⓐ Evaluate p ( − 3 ) . p ( − 3 ) .
- ⓑ Solve p ( c ) = 2. p ( c ) = 2.
Given the function f ( x ) = x 2 − 3 x : f ( x ) = x 2 − 3 x :
- ⓐ Evaluate f ( 5 ) . f ( 5 ) .
- ⓑ Solve f ( x ) = 4. f ( x ) = 4.
Given the function f ( x ) = x + 2 : f ( x ) = x + 2 :
- ⓐ Evaluate f ( 7 ) . f ( 7 ) .
Consider the relationship 3 r + 2 t = 18. 3 r + 2 t = 18.
- ⓐ Write the relationship as a function r = f ( t ) . r = f ( t ) .
- ⓑ Evaluate f ( − 3 ) . f ( − 3 ) .
- ⓒ Solve f ( t ) = 2. f ( t ) = 2.
For the following exercises, use the vertical line test to determine which graphs show relations that are functions.
Given the following graph,
- ⓐ Evaluate f ( −1 ) . f ( −1 ) .
- ⓑ Solve for f ( x ) = 3. f ( x ) = 3.
- ⓐ Evaluate f ( 0 ) . f ( 0 ) .
- ⓑ Solve for f ( x ) = −3. f ( x ) = −3.
- ⓐ Evaluate f ( 4 ) . f ( 4 ) .
- ⓑ Solve for f ( x ) = 1. f ( x ) = 1.
For the following exercises, determine if the given graph is a one-to-one function.
{ ( −1 , −1 ) , ( −2 , −2 ) , ( −3 , −3 ) } { ( −1 , −1 ) , ( −2 , −2 ) , ( −3 , −3 ) }
{ ( 3 , 4 ) , ( 4 , 5 ) , ( 5 , 6 ) } { ( 3 , 4 ) , ( 4 , 5 ) , ( 5 , 6 ) }
{ ( 2 , 5 ) , ( 7 , 11 ) , ( 15 , 8 ) , ( 7 , 9 ) } { ( 2 , 5 ) , ( 7 , 11 ) , ( 15 , 8 ) , ( 7 , 9 ) }
For the following exercises, determine if the relation represented in table form represents y y as a function of x . x .
For the following exercises, use the function f f represented in the table below.
Evaluate f ( 3 ) . f ( 3 ) .
Solve f ( x ) = 1. f ( x ) = 1.
For the following exercises, evaluate the function f f at the values f ( − 2 ) , f ( − 1 ) , f ( 0 ) , f ( 1 ) , f ( − 2 ) , f ( − 1 ) , f ( 0 ) , f ( 1 ) , and f ( 2 ) . f ( 2 ) .
f ( x ) = 4 − 2 x f ( x ) = 4 − 2 x
f ( x ) = 8 − 3 x f ( x ) = 8 − 3 x
f ( x ) = 8 x 2 − 7 x + 3 f ( x ) = 8 x 2 − 7 x + 3
f ( x ) = 3 + x + 3 f ( x ) = 3 + x + 3
f ( x ) = x − 2 x + 3 f ( x ) = x − 2 x + 3
f ( x ) = 3 x f ( x ) = 3 x
For the following exercises, evaluate the expressions, given functions f , g , f , g , and h : h :
f ( x ) = 3 x − 2 f ( x ) = 3 x − 2 g ( x ) = 5 − x 2 g ( x ) = 5 − x 2 h ( x ) = − 2 x 2 + 3 x − 1 h ( x ) = − 2 x 2 + 3 x − 1
3 f ( 1 ) − 4 g ( − 2 ) 3 f ( 1 ) − 4 g ( − 2 )
f ( 7 3 ) − h ( − 2 ) f ( 7 3 ) − h ( − 2 )
For the following exercises, graph y = x 2 y = x 2 on the given domain. Determine the corresponding range. Show each graph.
[ − 0.1 , 0.1 ] [ − 0.1 , 0.1 ]
[ − 10 , 10 ] [ − 10 , 10 ]
[ − 100 , 100 ] [ − 100 , 100 ]
For the following exercises, graph y = x 3 y = x 3 on the given domain. Determine the corresponding range. Show each graph.
[ − 0.1 , 0 .1 ] [ − 0.1 , 0 .1 ]
For the following exercises, graph y = x y = x on the given domain. Determine the corresponding range. Show each graph.
[ 0 , 0 .01 ] [ 0 , 0 .01 ]
[ 0 , 100 ] [ 0 , 100 ]
[ 0 , 10,000 ] [ 0 , 10,000 ]
[ −0.001 , 0.001 ] [ −0.001 , 0.001 ]
[ −1000 , 1000 ] [ −1000 , 1000 ]
[ −1,000,000 , 1,000,000 ] [ −1,000,000 , 1,000,000 ]
Real-World Applications
The amount of garbage, G , G , produced by a city with population p p is given by G = f ( p ) . G = f ( p ) . G G is measured in tons per week, and p p is measured in thousands of people.
- ⓐ The town of Tola has a population of 40,000 and produces 13 tons of garbage each week. Express this information in terms of the function f . f .
- ⓑ Explain the meaning of the statement f ( 5 ) = 2. f ( 5 ) = 2.
The number of cubic yards of dirt, D , D , needed to cover a garden with area a a square feet is given by D = g ( a ) . D = g ( a ) .
- ⓐ A garden with area 5000 ft 2 requires 50 yd 3 of dirt. Express this information in terms of the function g . g .
- ⓑ Explain the meaning of the statement g ( 100 ) = 1. g ( 100 ) = 1.
Let f ( t ) f ( t ) be the number of ducks in a lake t t years after 1990. Explain the meaning of each statement:
- ⓐ f ( 5 ) = 30 f ( 5 ) = 30
- ⓑ f ( 10 ) = 40 f ( 10 ) = 40
Let h ( t ) h ( t ) be the height above ground, in feet, of a rocket t t seconds after launching. Explain the meaning of each statement:
- ⓐ h ( 1 ) = 200 h ( 1 ) = 200
- ⓑ h ( 2 ) = 350 h ( 2 ) = 350
Show that the function f ( x ) = 3 ( x − 5 ) 2 + 7 f ( x ) = 3 ( x − 5 ) 2 + 7 is underline not end underline one-to-one.
- 1 http://www.baseball-almanac.com/legendary/lisn100.shtml. Accessed 3/24/2014.
- 2 http://www.kgbanswers.com/how-long-is-a-dogs-memory-span/4221590. Accessed 3/24/2014.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/3-1-functions-and-function-notation
© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Common Core State Standards Initiative
High School: Algebra
Standards in this domain:, ccss.math.content.hsa.introduction introduction, expressions..
An expression is a record of a computation with numbers, symbols that represent numbers, arithmetic operations, exponentiation, and, at more advanced levels, the operation of evaluating a function. Conventions about the use of parentheses and the order of operations assure that each expression is unambiguous. Creating an expression that describes a computation involving a general quantity requires the ability to express the computation in general terms, abstracting from specific instances.
Reading an expression with comprehension involves analysis of its underlying structure. This may suggest a different but equivalent way of writing the expression that exhibits some different aspect of its meaning. For example, p + 0.05 p can be interpreted as the addition of a 5% tax to a price p . Rewriting p + 0.05 p as 1.05 p shows that adding a tax is the same as multiplying the price by a constant factor.
Algebraic manipulations are governed by the properties of operations and exponents, and the conventions of algebraic notation. At times, an expression is the result of applying operations to simpler expressions. For example, p + 0.05 p is the sum of the simpler expressions p and 0.05 p . Viewing an expression as the result of operation on simpler expressions can sometimes clarify its underlying structure.
A spreadsheet or a computer algebra system (CAS) can be used to experiment with algebraic expressions, perform complicated algebraic manipulations, and understand how algebraic manipulations behave.
Equations and inequalities.
An equation is a statement of equality between two expressions, often viewed as a question asking for which values of the variables the expressions on either side are in fact equal. These values are the solutions to the equation. An identity, in contrast, is true for all values of the variables; identities are often developed by rewriting an expression in an equivalent form.
The solutions of an equation in one variable form a set of numbers; the solutions of an equation in two variables form a set of ordered pairs of numbers, which can be plotted in the coordinate plane. Two or more equations and/or inequalities form a system. A solution for such a system must satisfy every equation and inequality in the system.
An equation can often be solved by successively deducing from it one or more simpler equations. For example, one can add the same constant to both sides without changing the solutions, but squaring both sides might lead to extraneous solutions. Strategic competence in solving includes looking ahead for productive manipulations and anticipating the nature and number of solutions.
Some equations have no solutions in a given number system, but have a solution in a larger system. For example, the solution of x + 1 = 0 is an integer, not a whole number; the solution of 2 x + 1 = 0 is a rational number, not an integer; the solutions of x 2 - 2 = 0 are real numbers, not rational numbers; and the solutions of x 2 + 2 = 0 are complex numbers, not real numbers.
The same solution techniques used to solve equations can be used to rearrange formulas. For example, the formula for the area of a trapezoid, A = (( b 1 + b 2 )/2) h , can be solved for h using the same deductive process. Inequalities can be solved by reasoning about the properties of inequality. Many, but not all, of the properties of equality continue to hold for inequalities and can be useful in solving them.
Connections to Functions and Modeling. Expressions can define functions, and equivalent expressions define the same function. Asking when two functions have the same value for the same input leads to an equation; graphing the two functions allows for finding approximate solutions of the equation. Converting a verbal description to an equation, inequality, or system of these is an essential skill in modeling.
Algebra Overview
- Seeing Structure in Expressions
- Interpret the structure of expressions
- Write expressions in equivalent forms to solve problems
Arithmetic with Polynomials and Rational Functions
- Perform arithmetic operations on polynomials
- Understand the relationship between zeros and factors of polynomials
- Use polynomial identities to solve problems
- Rewrite rational functions
Creating Equations
- Create equations that describe numbers or relationships
Reasoning with Equations and Inequalities
- Understand solving equations as a process of reasoning and explain the reasoning
- Solve equations and inequalities in one variable
- Solve systems of equations
- Represent and solve equations and inequalities graphically
Mathematical Practices
- Make sense of problems and persevere in solving them.
- Reason abstractly and quantitatively.
- Construct viable arguments and critique the reasoning of others.
- Model with mathematics.
- Use appropriate tools strategically.
- Attend to precision.
- Look for and make use of structure.
- Look for and express regularity in repeated reasoning.
Arithmetic with Polynomials & Rational Expressions
Creating equations ✭, reasoning with equations & inequalities.
- Standards for Mathematical Practice
- How to read the grade level standards
- Introduction
- Counting & Cardinality
- Operations & Algebraic Thinking
- Number & Operations in Base Ten
- Measurement & Data
- Number & Operations—Fractions¹
- Number & Operations in Base Ten¹
- Number & Operations—Fractions
- Ratios & Proportional Relationships
- The Number System
- Expressions & Equations
- Statistics & Probability
- The Real Number System
- Quantities*
- The Complex Number System
- Vector & Matrix Quantities
- Arithmetic with Polynomials & Rational Expressions
- Creating Equations*
- Reasoning with Equations & Inequalities
- Interpreting Functions
- Building Functions
- Linear, Quadratic, & Exponential Models*
- Trigonometric Functions
- High School: Modeling
- Similarity, Right Triangles, & Trigonometry
- Expressing Geometric Properties with Equations
- Geometric Measurement & Dimension
- Modeling with Geometry
- Interpreting Categorical & Quantitative Data
- Making Inferences & Justifying Conclusions
- Conditional Probability & the Rules of Probability
- Using Probability to Make Decisions
- Courses & Transitions
- Mathematics Glossary
- Mathematics Appendix A

- Share on Facebook
- Tweet This Resource
- Pin This Resource

Common Core Algebra 1, Unit 8: Functions
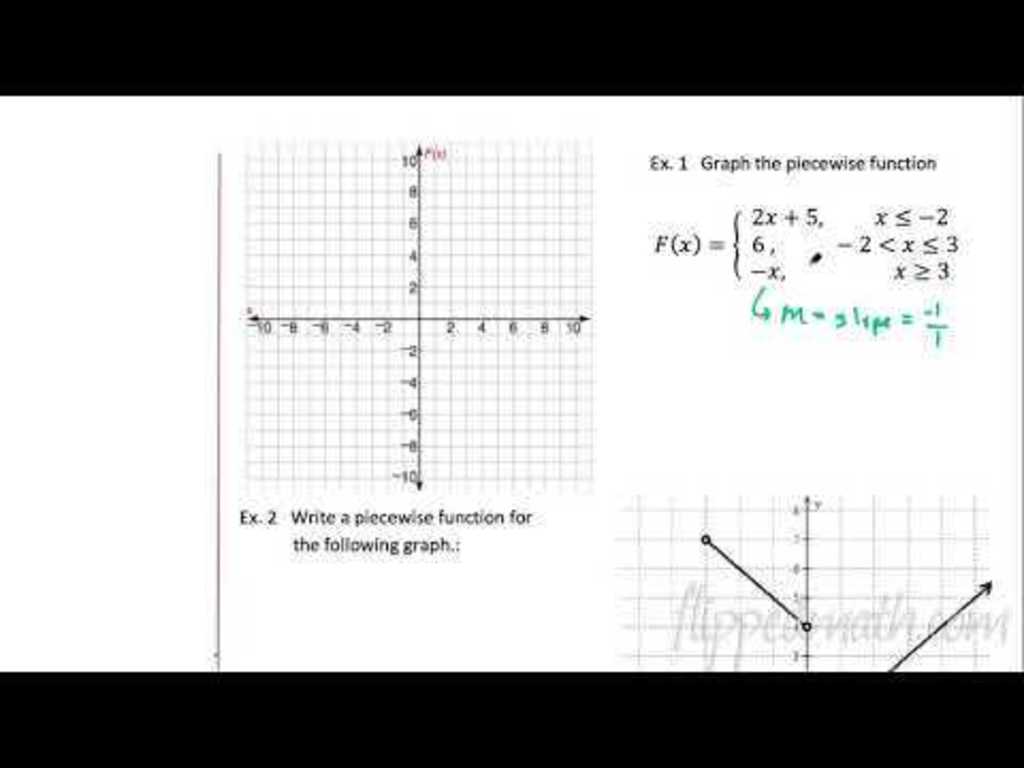
Four lessons make up Unit 8 in the Flipped Math Algebra 1 module. Each lesson contains an instructional video, practice sets, and corrective assignments. The first lesson looks at function notation, domain, and range. The video presentation uses grocery store prices as an example to explain the concept of a function. Pupils determine whether mappings are functions or not and find the domain and range. They evaluate functions with different inputs expressed in function notation. Next, pupils watch a video presentation starting with vocabulary on properties of a graph of a function. They then use the vocabulary to find key features of graphs of a function. The third lesson in the series teaches viewers how to graph and determine the equation and values of piecewise functions. The fourth has scholars using a graphing calculator to find the solution to an equation in one variable. The Unit 8 review has pupils work through 31 items to review the concepts learned in the unit. Scholars determine whether a mapping is a function and identify the domain and range. Using function notation, individuals then evaluate functions to solve problems. They also use graphs to find key features of functions, solve equations, and display piecewise functions.
Common Core

Functions, Domain and Range

Practice Packet (.pdf)

Practice Solutions (.pdf)

Corrective Assignment (.pdf)

Functions, Domain and Range (.mp4)
Graphs of Functions
Graphs of Functions (.mp4)
Piecewise Functions
Piecewise Functions (.mp4)
Graphing Functions to Solve Equations

Graphing Functions to Solve Equations (.mp4)

Unit 8 Review: Functions

Unit 8 Review: Functions (.html)
Introduction to Common Core Algebra - 1
Algebra 1 is the first of the five high-school courses (Algebra 1, Geometry, Algebra 2, Precalculus, and Calculus) and is typically taken in grade 9. However, some students take it in grade 7 or 8 so as to enable them to take Calculus or another college-level course in their senior high-school year.
The contents of Algebra 1 are divided among the following four domains:
- Expressions, Equations, and Inequalities
Now, while the standards covered under the Numbers and Statistics domains are more of an extension of the corresponding grade 8 ones, those under the Equations and Functions domains introduce the student to many big mathematical ideas. Let’s take a look at some of the big ideas from these two domains and how the standards approach them.
Expressions, Equations and Inequalities
The standards in this domain recap a lot of the Algebra that is learned through middle school. However, in addition to procedural fluency, the focus here is on explaining the reasoning.
For example, the standard process of solving a linear inequality in two variables, say $$2x + 4y < 12$$ involves dividing the XY-plane into two regions using its boundary line $$2x + 4y = 12$$
Then, the region which represents the solution is identified by considering test points in both regions. However, this process is rather mechanical and the reasoning behind isn’t usually explained. So, to help the student understand this intuitively, the standards recommend building on their existing knowledge of linear equations.
To do this, we would isolate the y in $$2x + 4y < 12$$ on its LHS, and rewrite it as $$y < 3 - \frac{1}{2}x$$
Now, the boundary line is $$y = 3 - \frac{1}{2}x$$ and this helps the student understand that, for a given x-value:
- if y is less than $$3 - \frac{1}{2}x$$ then (x, y) must lie below the boundary line.
- if y equals $$3 - \frac{1}{2}x$$ then (x, y) must lie on the boundary line.
- if y is greater than $$3 - \frac{1}{2}x$$ then (x, y) must lie above the boundary line.
To make this even clearer, the boundary line and a vertical line, say x = 4, and can be graphed as follows:
Here, when x = 4, $$3 - \frac{1}{2}x$$ equals $$3 - \frac{1}{2}(4)$$ or $$1$$
Hence, the line x = 4 intersects the boundary line at (4, 1) as shown above. Now, of the other points on the line x = 4:
- the ones whose y-coordinate is less than 1 lie below the boundary line.
- the ones whose y-coordinate is greater than 1 lie above the boundary line.
Similarly, for any point (x, y) to represent a solution to $$y < 3 - \frac{1}{2}x$$ it must lie below the boundary line $$y= 3 - \frac{1}{2}x$$
Thus, we show that the region below the boundary line is the solution to the given inequality.
This domain forms the bulk of the Algebra 1 course. The standards included here formalize the student’s middle-school-understanding of functions by introducing them to the function notation and the ideas of the domain and range. This is a super-important domain on which a large chunk of more advanced high-school Math is based.
To facilitate the development of an intuitive and deep conceptual understanding of the big ideas involved here, the standards recommend the use of a variety of visual-aids as follows:
Representation : The standards recommend giving the student ample exposure to switching among different representations of a function. For example, to get a visual sense of the relationship between the input and output of a function, it is important to start with:
- its algebraic representation, say f(x) = x 2 , move on to
- a tabular representation listing out a few of its input-output pairs, and finally to
- a graphical representation by plotting and joining the input-output pairs on a graph.
This sort of approach helps the student appreciate the interconnectedness of different forms of representation, and understand their advantages and disadvantages. It also helps them see how a graphical representation can be useful for a qualitative comparison between two functions covering parameters like their rates of changes, increasing/decreasing intervals, etc.
Key Features of the Graph : Most textbooks treat the key features of the graph of a function, e.g. its shape, intercepts, maximum/minimum values, etc., in isolation. As a result, the student is often unable to link the algebraic and geometric interpretations of a given function. For example, consider the graph of the function f(x) = x 2 - 6x +6 as follows:
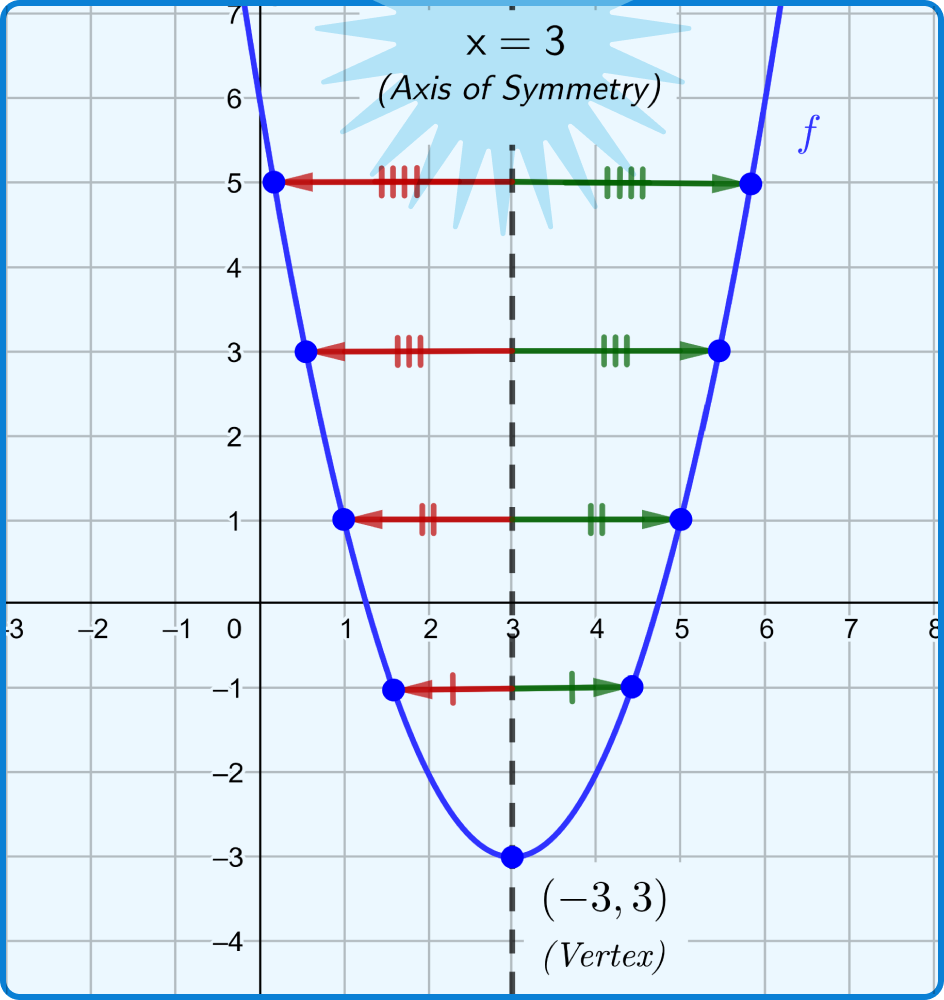
To understand why this graph is U-shaped , we can rewrite its function rule in the vertex form, i.e. f(x) = (x - 3) 2 - 3. This makes it easy to recognize that:
- The point (3, -3) is the lowest on the graph because that’s where the value of (x-3) 2 is minimum , i.e., 0.
- The line x = 3 divides the graph into identical halves as the values of (x-3) 2 are equal for x-values equidistant from 3 (for e.g., x = 1 and x = 5). Hence, the values of f(x) = (x-3) 2 - 3 are also equal for such x-values, and as a result, the graph is U-shaped.
Transformations : This is a problem-area for a lot of students as they try to commit a few formulas to memory, and then use them to solve problems. As a result, they are thrown off-guard by small changes in the way the question is worded and/or by a difference in the context. To avoid this, there is a comprehensive set of standards that are geared towards understanding the algebraic rationale behind the graphical relationships of functions like f(x) + k, kf(x), and f(kx) with f(x).
The Cuemath curriculum provides learning experiences of important concepts through concrete and pictorial representations and connects mathematics with the lives of students. Cuemath conducts Live Online Math classes . This makes the students love math and see its relevance in their day to day lives.
-By Rigved Jhunjhunwala

Function Notation Common Core Algebra I Homework Fluency 1. Given the function ∫ defined by the formula f(x)=2x+1 find the following: (a) f(4) (b) f(-5) f(0) (d) f( 1/2 ) (c) 2. Given the function g defined by the formula g(x)= (x-5)/2 find the following: (a) g(9) (b) g(0) (c) g(3) (d) g(17)

IMAGES
VIDEO
COMMENTS
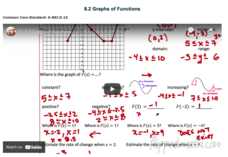
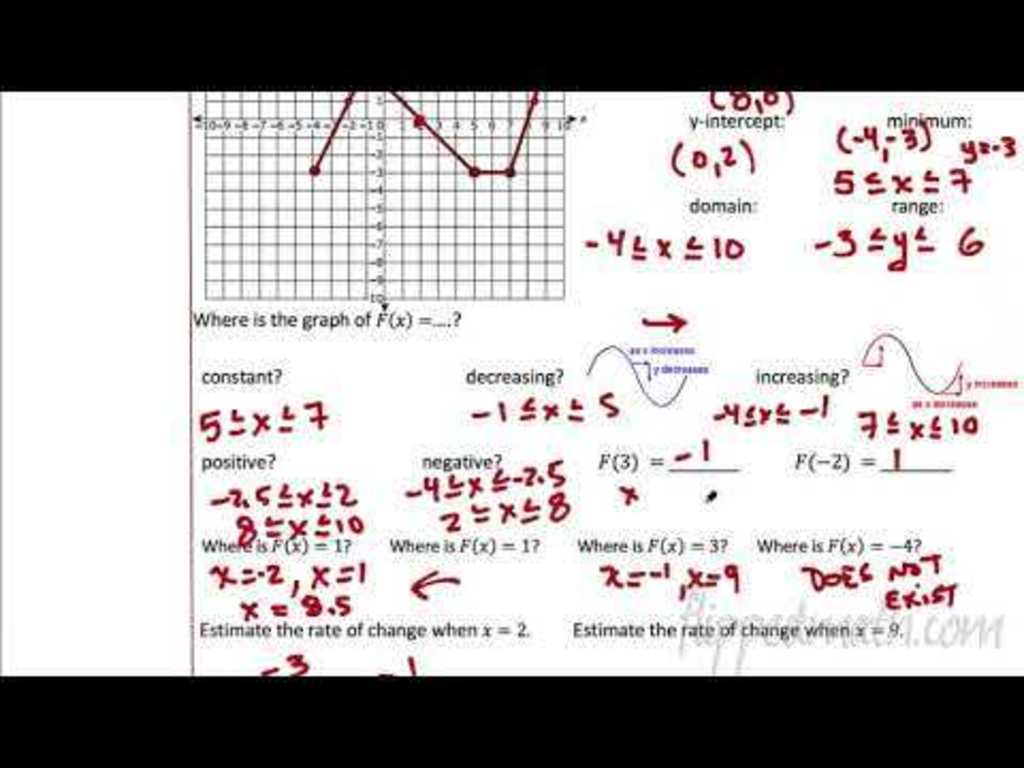
Unit 3 - Functions. In this unit we review the basic concept of a function and emphasize multiple representations of these foundational tools. Graphical features of functions, including maximums, minimums, intervals of increase and decrease along with domain and range are introduced. Classic function notation is used throughout the unit.
In this lesson we learn the classic f(x) notation for function rules. Equation, table, and graphical function representations are used. Solving for inputs ...
Lesson 16: Graphing Quadratic Equations From the Vertex Form, y=a (x-h) 2 +k ( Vide0) Lesson 17: Graphing Quadratic Functions From the Standard Form, f (x)=ax 2 +bx+c ( Video Lesson) Function Transformations and Modeling. Topic C Overview. Lesson 18: Graphing Cubic, Square Root, and Cube Root Functions.
Representing Functions Using Tables. A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases, these values represent all we know about the relationship; other times, the table provides a few select examples from a more complete relationship.
Find step-by-step solutions and answers to Algebra 1 Common Core - 9780133185485, as well as thousands of textbooks so you can move forward with confidence. ... Patterns and Linear Functions. Section 4-3: Patterns and Nonlinear Functions. Page 252: Mid-Chapter Quiz. Section 4-4: Graphing a Function Rule. Section 4-5: Writing a Function Rule ...
amount of money, A, in his account as a function of the number of years, t, since creating the account is given by the equation At 2500 1.04 t. (a) Evaluate AA 0 and 10 . x 17.5 17.6 17.8 5. A ball is shot from an air-cannon at an angle of 45 with the horizon. It travels along a path given by the equation 1 2 50 h d d d
Students are introduced to the definition of a function and the various ways they can be represented. For the worksheet used in this lesson, click on:http://...
The X intercepts are where Y is equal to zero, and that occurs at X equals one, two, three, four, 5, 6, at X equals negative 6, and at X equals one, two, three, four, negative four. All right. The zeros of a function are where the output of the function is equal to zero. The X values where the output is equal to zero.
We are so glad that you are taking responsibility for your education in Algebra I. SEMESTER 1. UNIT 1: Analyze Graphs and Expressions. UNIT 2: Create and Solve Equations/Ineq. UNIT 3: Systems of Equations. UNIT 4: One Variable Statistics. UNIT 5: Analyze Two Variable Data. UNIT 6: Sequences. SEMESTER 2.
CCSS.Math.Content.HSA.REI.A.1. Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, starting from the assumption that the original equation has a solution. Construct a viable argument to justify a solution method. CCSS.Math.Content.HSA.REI.A.2.
Common Core Algebra 1, Unit 8: Functions. Four lessons make up Unit 8 in the Flipped Math Algebra 1 module. Each lesson contains an instructional video, practice sets, and corrective assignments. The first lesson looks at function notation, domain, and range. The video presentation uses grocery store prices as an example to explain the concept ...
Functions. This domain forms the bulk of the Algebra 1 course. The standards included here formalize the student's middle-school-understanding of functions by introducing them to the function notation and the ideas of the domain and range. This is a super-important domain on which a large chunk of more advanced high-school Math is based.
Algebra 1 Common Core: Home List of Lessons Semester 1 > > > > > > > Semester 2 > > > > > Teacher Resources 8.1 Functions, Domain and Range. Common ... 8.1 Functions, Domain and Range. Common Core Standard: HSF-IF.A.1 . Packet. To purchase this lesson packet, or the entire course's lesson, please click here.
This first unit is devoted to the development of functions as building blocks of higher-level mathematics. Simple functions are explored in algebraic, graphical, and tabular forms. Graphing calculator technology is utilized to quickly visualize graphs of functions and their tabular behavior. Preliminary concepts concerning one-to-one and ...
Function Notation Common Core Algebra I Homework Fluency 1. Given the function ∫ defined by the formula f(x)=2x+1 find the following: (a) f(4) (b) f(-5) f(0) (d) f( 1/2 ) (c) 2. Given the function g defined by the formula g(x)= (x-5)/2 find the following: (a) g(9) (b) g(0) (c) g(3) (d) g(17)
REASONING. 4. In one of the following tables, the variable y is a function of the variable x. Explain which relationship is a function and why the other is not. Relationship #1 is a function because each input value, x, is paired with a single output variable, y. Relationship #2 is not a function because there are multiple inputs, , which have ...
Standards Alignment - Powered by EdGate. Table of Contents for Common Core Algebra I. Unit 1 - The Building Blocks of Algebra. Unit 2 - Linear Expressions, Equations, and Inequalities. Unit 3 - Functions. Unit 4 - Linear Functions and Arithmetic Sequences. Unit 5 - Systems of Linear Equations and Inequalities.
Sequences & Series Notes & Homework Packet Lesson 1: Sequences Sequences are ordered lists of numbers. A sequence is formally defined as a function that has its domain the set of positive integers, i.e. {1, 2, 3, …, n}. Exercise 1: A sequence is defined by the ... In Common Core Algebra 1, you studied two particular sequences known as ...
Hello and welcome to another common core algebra two lesson by E math instruction. My name is Kirk weiler, and today we're going to be doing unit number two lesson number two on function notation. So function notation is something that you saw back in common core algebra one, but you probably didn't use that much in common core geometry.
Hello and welcome to another common core algebra two lesson. By E math instruction. My name is Kirk Weiler, and today we're going to be doing unit two lesson number three on composite on function composition. Function composition is a very, very important topic, and you are ready for it at this level. The idea is very simple.
• Lesson #2 - Function Notation • Lesson #3 - Function Composition • Lesson #4 - The Domain and Range of a Function • Lesson #5 - One to One Functions ... The Method of Common Bases • Lesson #6 - Exponential Modeling with Percent Growth and Decay • Lesson #7 - Mindful Percent Manipulations ...
Common Core Algebra I; Common Core Geometry; Common Core Algebra II; Algebra 2 + Trigonometry; For Teachers. N-Gen Math™ 6; N-Gen Math™ 7; N-Gen Math™ 8; N-Gen Math™ Algebra I; N-Gen Math Algebra II; N-Gen Math™ Geometry; Common Core Algebra I; Common Core Geometry; Common Core Algebra II; Algebra 2 + Trigonometry; Standards Alignment ...
Common Core Algebra I; Common Core Geometry; Common Core Algebra II; Algebra 2 + Trigonometry; Efofex; eMATH Merch; ... LESSON/HOMEWORK. LESSON VIDEO. ANSWER KEY. EDITABLE LESSON. EDITABLE KEY. Lesson 3 ... Function Notation Practice RESOURCE. ANSWER KEY. EDITABLE RESOURCE. EDITABLE KEY.