quadratic equations homework 2 graphing quadratic equations

Graphing Quadratic Equations

Here is an example:

You can graph a Quadratic Equation using the Function Grapher , but to really understand what is going on, you can make the graph yourself. Read On!

The Simplest Quadratic

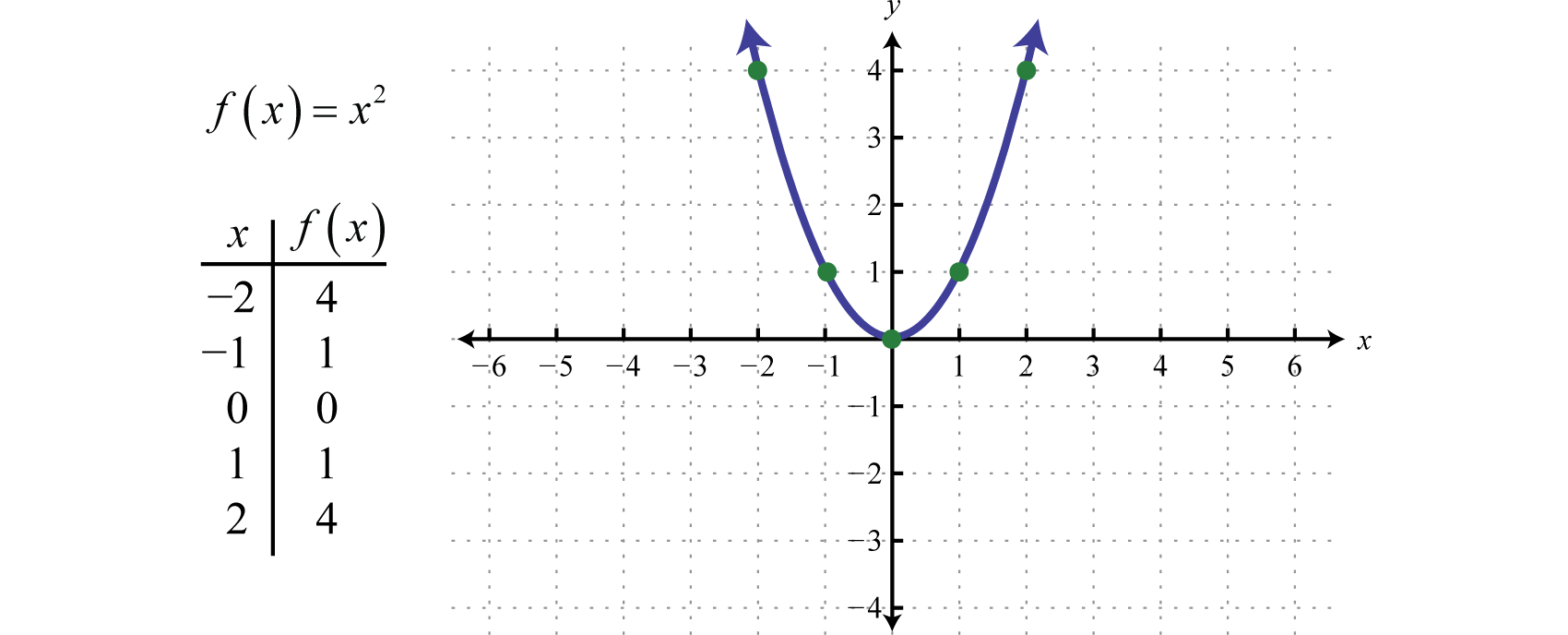
The simplest Quadratic Equation is:

And its graph is simple too:

This is the curve f(x) = x 2 It is a parabola .

Now let us see what happens when we introduce the "a" value:

f(x) = ax 2

• Larger values of a squash the curve inwards
• Smaller values of a expand it outwards
• And negative values of a flip it upside down

The "General" Quadratic

Before graphing we rearrange the equation, from this:

f(x) = ax 2 + bx + c

f(x) = a(x-h) 2 + k

In other words, calculate h (= −b/2a), then find k by calculating the whole equation for x=h

The wonderful thing about this new form is that h and k show us the very lowest (or very highest) point, called the vertex :

And also the curve is symmetrical (mirror image) about the axis that passes through x=h , making it easy to graph

• h shows us how far left (or right) the curve has been shifted from x=0
• k shows us how far up (or down) the curve has been shifted from y=0

Lets see an example of how to do this:

Example: Plot f(x) = 2x 2 − 12x + 16

First, let's note down:

• b = −12, and

Now, what do we know?

• a is positive, so it is an "upwards" graph ("U" shaped)
• a is 2, so it is a little "squashed" compared to the x 2 graph

Next, let's calculate h:

And next we can calculate k (using h=3):

So now we can plot the graph (with real understanding!):

We also know: the vertex is (3,−2), and the axis is x=3

From A Graph to The Equation

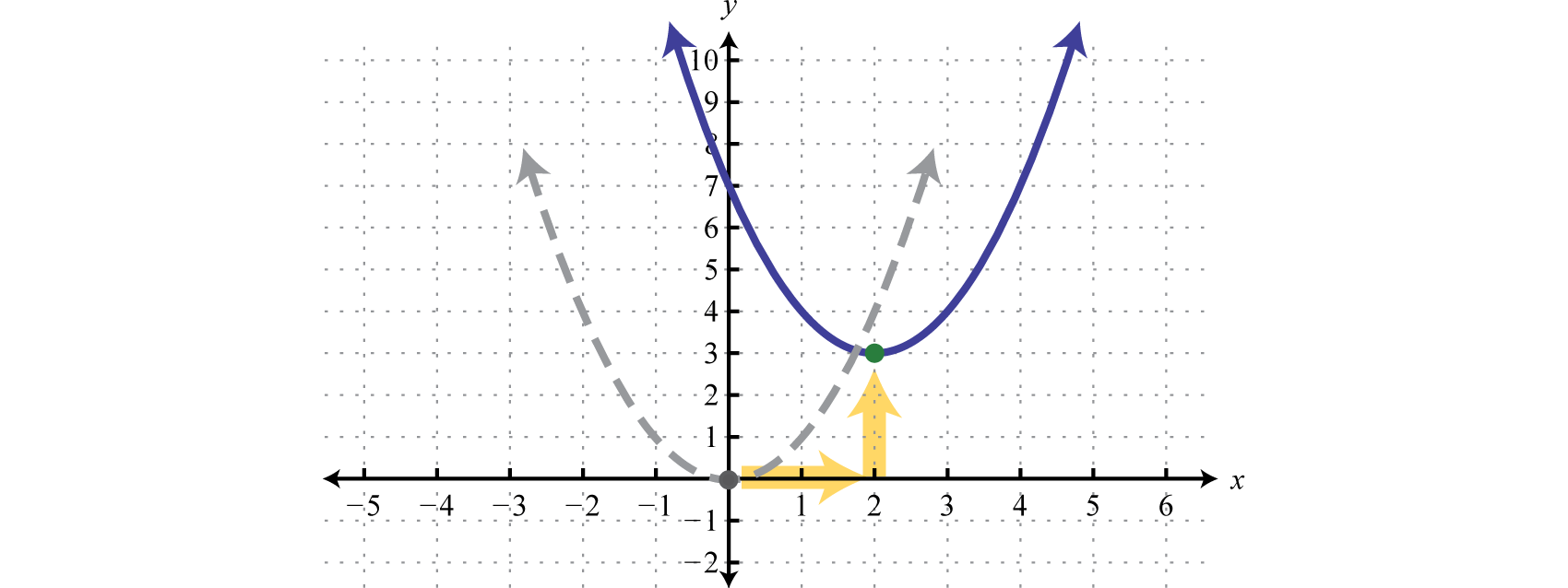
What if we have a graph, and want to find an equation?

Example: you have just plotted some interesting data, and it looks Quadratic:

Just knowing those two points we can come up with an equation.

Firstly, we know h and k (at the vertex):

(h, k) = (1, 1)

So let's put that into this form of the equation:

f(x) = a(x−1) 2 + 1

Then we calculate "a":

And here is the resulting Quadratic Equation:

f(x) = 0.5(x−1) 2 + 1

Note: This may not be the correct equation for the data, but it’s a good model and the best we can come up with.

2.5 Quadratic Equations

Learning objectives.

In this section, you will:

• Solve quadratic equations by factoring.
• Solve quadratic equations by the square root property.
• Solve quadratic equations by completing the square.
• Solve quadratic equations by using the quadratic formula.

The computer monitor on the left in Figure 1 is a 23.6-inch model and the one on the right is a 27-inch model. Proportionally, the monitors appear very similar. If there is a limited amount of space and we desire the largest monitor possible, how do we decide which one to choose? In this section, we will learn how to solve problems such as this using four different methods.

• Solving Quadratic Equations by Factoring

An equation containing a second-degree polynomial is called a quadratic equation . For example, equations such as 2 x 2 + 3 x − 1 = 0 2 x 2 + 3 x − 1 = 0 and x 2 − 4 = 0 x 2 − 4 = 0 are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics.

Often the easiest method of solving a quadratic equation is factoring . Factoring means finding expressions that can be multiplied together to give the expression on one side of the equation.

If a quadratic equation can be factored, it is written as a product of linear terms. Solving by factoring depends on the zero-product property, which states that if a ⋅ b = 0 , a ⋅ b = 0 , then a = 0 a = 0 or b = 0 , b = 0 , where a and b are real numbers or algebraic expressions. In other words, if the product of two numbers or two expressions equals zero, then one of the numbers or one of the expressions must equal zero because zero multiplied by anything equals zero.

Multiplying the factors expands the equation to a string of terms separated by plus or minus signs. So, in that sense, the operation of multiplication undoes the operation of factoring. For example, expand the factored expression ( x − 2 ) ( x + 3 ) ( x − 2 ) ( x + 3 ) by multiplying the two factors together.

The product is a quadratic expression. Set equal to zero, x 2 + x − 6 = 0 x 2 + x − 6 = 0 is a quadratic equation. If we were to factor the equation, we would get back the factors we multiplied.

The process of factoring a quadratic equation depends on the leading coefficient, whether it is 1 or another integer. We will look at both situations; but first, we want to confirm that the equation is written in standard form, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , where a , b , and c are real numbers, and a ≠ 0. a ≠ 0. The equation x 2 + x − 6 = 0 x 2 + x − 6 = 0 is in standard form.

We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF), and for equations that have special factoring formulas as well, such as the difference of squares, both of which we will see later in this section.

The Zero-Product Property and Quadratic Equations

The zero-product property states

where a and b are real numbers or algebraic expressions.

A quadratic equation is an equation containing a second-degree polynomial; for example

where a , b , and c are real numbers, and if a ≠ 0 , a ≠ 0 , it is in standard form.

Solving Quadratics with a Leading Coefficient of 1

In the quadratic equation x 2 + x − 6 = 0 , x 2 + x − 6 = 0 , the leading coefficient, or the coefficient of x 2 , x 2 , is 1. We have one method of factoring quadratic equations in this form.

Given a quadratic equation with the leading coefficient of 1, factor it.

• Find two numbers whose product equals c and whose sum equals b .
• Use those numbers to write two factors of the form ( x + k ) or  ( x − k ) , ( x + k ) or  ( x − k ) , where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and −2 , −2 , the factors are ( x + 1 ) ( x − 2 ) . ( x + 1 ) ( x − 2 ) .
• Solve using the zero-product property by setting each factor equal to zero and solving for the variable.

Factoring and Solving a Quadratic with Leading Coefficient of 1

Factor and solve the equation: x 2 + x − 6 = 0. x 2 + x − 6 = 0.

To factor x 2 + x − 6 = 0 , x 2 + x − 6 = 0 , we look for two numbers whose product equals −6 −6 and whose sum equals 1. Begin by looking at the possible factors of −6. −6.

The last pair, 3 ⋅ ( −2 ) 3 ⋅ ( −2 ) sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.

To solve this equation, we use the zero-product property. Set each factor equal to zero and solve.

The two solutions are 2 2 and −3. −3. We can see how the solutions relate to the graph in Figure 2 . The solutions are the x- intercepts of y = x 2 + x − 6 = 0. y = x 2 + x − 6 = 0.

Factor and solve the quadratic equation: x 2 − 5 x − 6 = 0. x 2 − 5 x − 6 = 0.

Solve the Quadratic Equation by Factoring

Solve the quadratic equation by factoring: x 2 + 8 x + 15 = 0. x 2 + 8 x + 15 = 0.

Find two numbers whose product equals 15 15 and whose sum equals 8. 8. List the factors of 15. 15.

The numbers that add to 8 are 3 and 5. Then, write the factors, set each factor equal to zero, and solve.

The solutions are −3 −3 and −5. −5.

Solve the quadratic equation by factoring: x 2 − 4 x − 21 = 0. x 2 − 4 x − 21 = 0.

Using the Zero-Product Property to Solve a Quadratic Equation Written as the Difference of Squares

Solve the difference of squares equation using the zero-product property: x 2 − 9 = 0. x 2 − 9 = 0.

Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property.

The solutions are 3 3 and −3. −3.

Solve by factoring: x 2 − 25 = 0. x 2 − 25 = 0.

Solving a Quadratic Equation by Factoring when the Leading Coefficient is not 1

When the leading coefficient is not 1, we factor a quadratic equation using the method called grouping, which requires four terms. With the equation in standard form, let’s review the grouping procedures:

• With the quadratic in standard form, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , multiply a ⋅ c . a ⋅ c .
• Find two numbers whose product equals a c a c and whose sum equals b . b .
• Rewrite the equation replacing the b x b x term with two terms using the numbers found in step 2 as coefficients of x.
• Factor the first two terms and then factor the last two terms. The expressions in parentheses must be exactly the same to use grouping.
• Factor out the expression in parentheses.
• Set the expressions equal to zero and solve for the variable.

Solving a Quadratic Equation Using Grouping

Use grouping to factor and solve the quadratic equation: 4 x 2 + 15 x + 9 = 0. 4 x 2 + 15 x + 9 = 0.

First, multiply a c : 4 ( 9 ) = 36. a c : 4 ( 9 ) = 36. Then list the factors of 36. 36.

The only pair of factors that sums to 15 15 is 3 + 12. 3 + 12. Rewrite the equation replacing the b term, 15 x , 15 x , with two terms using 3 and 12 as coefficients of x . Factor the first two terms, and then factor the last two terms.

Solve using the zero-product property.

The solutions are − 3 4 , − 3 4 , and −3. −3. See Figure 3 .

Solve using factoring by grouping: 12 x 2 + 11 x + 2 = 0. 12 x 2 + 11 x + 2 = 0.

Solving a Polynomial of Higher Degree by Factoring

Solve the equation by factoring: −3 x 3 − 5 x 2 − 2 x = 0. −3 x 3 − 5 x 2 − 2 x = 0.

This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out − x − x from all of the terms and then proceed with grouping.

Use grouping on the expression in parentheses.

Now, we use the zero-product property. Notice that we have three factors.

The solutions are 0 , 0 , − 2 3 , − 2 3 , and −1. −1.

Solve by factoring: x 3 + 11 x 2 + 10 x = 0. x 3 + 11 x 2 + 10 x = 0.

Using the Square Root Property

When there is no linear term in the equation, another method of solving a quadratic equation is by using the square root property , in which we isolate the x 2 x 2 term and take the square root of the number on the other side of the equals sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the x 2 x 2 term so that the square root property can be used.

The Square Root Property

With the x 2 x 2 term isolated, the square root property states that:

where k is a nonzero real number.

Given a quadratic equation with an x 2 x 2 term but no x x term, use the square root property to solve it.

• Isolate the x 2 x 2 term on one side of the equal sign.
• Take the square root of both sides of the equation, putting a ± ± sign before the expression on the side opposite the squared term.
• Simplify the numbers on the side with the ± ± sign.

Solving a Simple Quadratic Equation Using the Square Root Property

Solve the quadratic using the square root property: x 2 = 8. x 2 = 8.

Take the square root of both sides, and then simplify the radical. Remember to use a ± ± sign before the radical symbol.

The solutions are 2 2 , 2 2 , −2 2 . −2 2 .

Solving a Quadratic Equation Using the Square Root Property

Solve the quadratic equation: 4 x 2 + 1 = 7. 4 x 2 + 1 = 7.

First, isolate the x 2 x 2 term. Then take the square root of both sides.

The solutions are 6 2 , 6 2 , and − 6 2 . − 6 2 .

Solve the quadratic equation using the square root property: 3 ( x − 4 ) 2 = 15. 3 ( x − 4 ) 2 = 15.

• Completing the Square

Not all quadratic equations can be factored or can be solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square . Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property. To complete the square, the leading coefficient, a , must equal 1. If it does not, then divide the entire equation by a . Then, we can use the following procedures to solve a quadratic equation by completing the square.

We will use the example x 2 + 4 x + 1 = 0 x 2 + 4 x + 1 = 0 to illustrate each step.

Given a quadratic equation that cannot be factored, and with a = 1 , a = 1 , first add or subtract the constant term to the right side of the equal sign.

Multiply the b term by 1 2 1 2 and square it.

Add ( 1 2 b ) 2 ( 1 2 b ) 2 to both sides of the equal sign and simplify the right side. We have

The left side of the equation can now be factored as a perfect square.

Use the square root property and solve.

The solutions are −2 + 3 , −2 + 3 , and −2 − 3 . −2 − 3 .

Solving a Quadratic by Completing the Square

Solve the quadratic equation by completing the square: x 2 − 3 x − 5 = 0. x 2 − 3 x − 5 = 0.

First, move the constant term to the right side of the equal sign.

Then, take 1 2 1 2 of the b term and square it.

Add the result to both sides of the equal sign.

Factor the left side as a perfect square and simplify the right side.

The solutions are 3 + 29 2 3 + 29 2 and 3 - 29 2 3 - 29 2 .

Solve by completing the square: x 2 − 6 x = 13. x 2 − 6 x = 13.

Using the Quadratic Formula

The fourth method of solving a quadratic equation is by using the quadratic formula , a formula that will solve all quadratic equations. Although the quadratic formula works on any quadratic equation in standard form, it is easy to make errors in substituting the values into the formula. Pay close attention when substituting, and use parentheses when inserting a negative number.

We can derive the quadratic formula by completing the square . We will assume that the leading coefficient is positive; if it is negative, we can multiply the equation by −1 −1 and obtain a positive a . Given a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , a ≠ 0 , a ≠ 0 , we will complete the square as follows:

First, move the constant term to the right side of the equal sign:

As we want the leading coefficient to equal 1, divide through by a :

Then, find 1 2 1 2 of the middle term, and add ( 1 2 b a ) 2 = b 2 4 a 2 ( 1 2 b a ) 2 = b 2 4 a 2 to both sides of the equal sign:

Next, write the left side as a perfect square. Find the common denominator of the right side and write it as a single fraction:

Now, use the square root property, which gives

Finally, add − b 2 a − b 2 a to both sides of the equation and combine the terms on the right side. Thus,

The Quadratic Formula

Written in standard form, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , any quadratic equation can be solved using the quadratic formula :

where a , b , and c are real numbers and a ≠ 0. a ≠ 0.

Given a quadratic equation, solve it using the quadratic formula

• Make sure the equation is in standard form: a x 2 + b x + c = 0. a x 2 + b x + c = 0.
• Make note of the values of the coefficients and constant term, a , b , a , b , and c . c .
• Carefully substitute the values noted in step 2 into the equation. To avoid needless errors, use parentheses around each number input into the formula.
• Calculate and solve.

Solve the Quadratic Equation Using the Quadratic Formula

Solve the quadratic equation: x 2 + 5 x + 1 = 0. x 2 + 5 x + 1 = 0.

Identify the coefficients: a = 1 , b = 5 , c = 1. a = 1 , b = 5 , c = 1. Then use the quadratic formula.

Solving a Quadratic Equation with the Quadratic Formula

Use the quadratic formula to solve x 2 + x + 2 = 0. x 2 + x + 2 = 0.

First, we identify the coefficients: a = 1 , b = 1 , a = 1 , b = 1 , and c = 2. c = 2.

Substitute these values into the quadratic formula.

The solutions to the equation are − 1 + i 7 2 − 1 + i 7 2 and − 1 − i 7 2 − 1 − i 7 2

Solve the quadratic equation using the quadratic formula: 9 x 2 + 3 x − 2 = 0. 9 x 2 + 3 x − 2 = 0.

The Discriminant

The quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions when we consider the discriminant , or the expression under the radical, b 2 − 4 a c . b 2 − 4 a c . The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. Table 1 relates the value of the discriminant to the solutions of a quadratic equation.

For a x 2 + b x + c = 0 a x 2 + b x + c = 0 , where a a , b b , and c c are real numbers, the discriminant is the expression under the radical in the quadratic formula: b 2 − 4 a c . b 2 − 4 a c . It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.

Using the Discriminant to Find the Nature of the Solutions to a Quadratic Equation

Use the discriminant to find the nature of the solutions to the following quadratic equations:

• ⓐ x 2 + 4 x + 4 = 0 x 2 + 4 x + 4 = 0
• ⓑ 8 x 2 + 14 x + 3 = 0 8 x 2 + 14 x + 3 = 0
• ⓒ 3 x 2 − 5 x − 2 = 0 3 x 2 − 5 x − 2 = 0
• ⓓ 3 x 2 − 10 x + 15 = 0 3 x 2 − 10 x + 15 = 0

Calculate the discriminant b 2 − 4 a c b 2 − 4 a c for each equation and state the expected type of solutions.

x 2 + 4 x + 4 = 0 x 2 + 4 x + 4 = 0

b 2 − 4 a c = ( 4 ) 2 − 4 ( 1 ) ( 4 ) = 0. b 2 − 4 a c = ( 4 ) 2 − 4 ( 1 ) ( 4 ) = 0. There will be one rational double solution.

8 x 2 + 14 x + 3 = 0 8 x 2 + 14 x + 3 = 0

b 2 − 4 a c = ( 14 ) 2 − 4 ( 8 ) ( 3 ) = 100. b 2 − 4 a c = ( 14 ) 2 − 4 ( 8 ) ( 3 ) = 100. As 100 100 is a perfect square, there will be two rational solutions.

3 x 2 − 5 x − 2 = 0 3 x 2 − 5 x − 2 = 0

b 2 − 4 a c = ( −5 ) 2 − 4 ( 3 ) ( −2 ) = 49. b 2 − 4 a c = ( −5 ) 2 − 4 ( 3 ) ( −2 ) = 49. As 49 49 is a perfect square, there will be two rational solutions.

3 x 2 −10 x + 15 = 0 3 x 2 −10 x + 15 = 0

b 2 − 4 a c = ( −10 ) 2 − 4 ( 3 ) ( 15 ) = −80. b 2 − 4 a c = ( −10 ) 2 − 4 ( 3 ) ( 15 ) = −80. There will be two complex solutions.

Using the Pythagorean Theorem

One of the most famous formulas in mathematics is the Pythagorean Theorem . It is based on a right triangle, and states the relationship among the lengths of the sides as a 2 + b 2 = c 2 , a 2 + b 2 = c 2 , where a a and b b refer to the legs of a right triangle adjacent to the 90° 90° angle, and c c refers to the hypotenuse. It has immeasurable uses in architecture, engineering, the sciences, geometry, trigonometry, and algebra, and in everyday applications.

We use the Pythagorean Theorem to solve for the length of one side of a triangle when we have the lengths of the other two. Because each of the terms is squared in the theorem, when we are solving for a side of a triangle, we have a quadratic equation. We can use the methods for solving quadratic equations that we learned in this section to solve for the missing side.

The Pythagorean Theorem is given as

where a a and b b refer to the legs of a right triangle adjacent to the 90 ∘ 90 ∘ angle, and c c refers to the hypotenuse, as shown in Figure 4 .

Finding the Length of the Missing Side of a Right Triangle

Find the length of the missing side of the right triangle in Figure 5 .

As we have measurements for side b and the hypotenuse, the missing side is a.

Use the Pythagorean Theorem to solve the right triangle problem: Leg a measures 4 units, leg b measures 3 units. Find the length of the hypotenuse.

Access these online resources for additional instruction and practice with quadratic equations.

• The Zero-Product Property
• Quadratic Formula with Two Rational Solutions
• Length of a leg of a right triangle

2.5 Section Exercises

How do we recognize when an equation is quadratic?

When we solve a quadratic equation, how many solutions should we always start out seeking? Explain why when solving a quadratic equation in the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 we may graph the equation y = a x 2 + b x + c y = a x 2 + b x + c and have no zeroes ( x -intercepts).

When we solve a quadratic equation by factoring, why do we move all terms to one side, having zero on the other side?

In the quadratic formula, what is the name of the expression under the radical sign b 2 − 4 a c , b 2 − 4 a c , and how does it determine the number of and nature of our solutions?

Describe two scenarios where using the square root property to solve a quadratic equation would be the most efficient method.

For the following exercises, solve the quadratic equation by factoring.

x 2 + 4 x − 21 = 0 x 2 + 4 x − 21 = 0

x 2 − 9 x + 18 = 0 x 2 − 9 x + 18 = 0

2 x 2 + 9 x − 5 = 0 2 x 2 + 9 x − 5 = 0

6 x 2 + 17 x + 5 = 0 6 x 2 + 17 x + 5 = 0

4 x 2 − 12 x + 8 = 0 4 x 2 − 12 x + 8 = 0

3 x 2 − 75 = 0 3 x 2 − 75 = 0

8 x 2 + 6 x − 9 = 0 8 x 2 + 6 x − 9 = 0

4 x 2 = 9 4 x 2 = 9

2 x 2 + 14 x = 36 2 x 2 + 14 x = 36

5 x 2 = 5 x + 30 5 x 2 = 5 x + 30

4 x 2 = 5 x 4 x 2 = 5 x

7 x 2 + 3 x = 0 7 x 2 + 3 x = 0

x 3 − 9 x = 2 x 3 − 9 x = 2

For the following exercises, solve the quadratic equation by using the square root property.

x 2 = 36 x 2 = 36

x 2 = 49 x 2 = 49

( x − 1 ) 2 = 25 ( x − 1 ) 2 = 25

( x − 3 ) 2 = 7 ( x − 3 ) 2 = 7

( 2 x + 1 ) 2 = 9 ( 2 x + 1 ) 2 = 9

( x − 5 ) 2 = 4 ( x − 5 ) 2 = 4

For the following exercises, solve the quadratic equation by completing the square. Show each step.

x 2 − 9 x − 22 = 0 x 2 − 9 x − 22 = 0

2 x 2 − 8 x − 5 = 0 2 x 2 − 8 x − 5 = 0

x 2 − 6 x = 13 x 2 − 6 x = 13

x 2 + 2 3 x − 1 3 = 0 x 2 + 2 3 x − 1 3 = 0

2 + z = 6 z 2 2 + z = 6 z 2

6 p 2 + 7 p − 20 = 0 6 p 2 + 7 p − 20 = 0

2 x 2 − 3 x − 1 = 0 2 x 2 − 3 x − 1 = 0

For the following exercises, determine the discriminant, and then state how many solutions there are and the nature of the solutions. Do not solve.

2 x 2 − 6 x + 7 = 0 2 x 2 − 6 x + 7 = 0

x 2 + 4 x + 7 = 0 x 2 + 4 x + 7 = 0

3 x 2 + 5 x − 8 = 0 3 x 2 + 5 x − 8 = 0

9 x 2 − 30 x + 25 = 0 9 x 2 − 30 x + 25 = 0

2 x 2 − 3 x − 7 = 0 2 x 2 − 3 x − 7 = 0

6 x 2 − x − 2 = 0 6 x 2 − x − 2 = 0

For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No Real Solution .

2 x 2 + 5 x + 3 = 0 2 x 2 + 5 x + 3 = 0

x 2 + x = 4 x 2 + x = 4

3 x 2 − 5 x + 1 = 0 3 x 2 − 5 x + 1 = 0

x 2 + 4 x + 2 = 0 x 2 + 4 x + 2 = 0

4 + 1 x − 1 x 2 = 0 4 + 1 x − 1 x 2 = 0

For the following exercises, enter the expressions into your graphing utility and find the zeroes to the equation (the x -intercepts) by using 2 nd CALC 2:zero . Recall finding zeroes will ask left bound (move your cursor to the left of the zero,enter), then right bound (move your cursor to the right of the zero,enter), then guess (move your cursor between the bounds near the zero, enter). Round your answers to the nearest thousandth.

Y 1 = 4 x 2 + 3 x − 2 Y 1 = 4 x 2 + 3 x − 2

Y 1 = −3 x 2 + 8 x − 1 Y 1 = −3 x 2 + 8 x − 1

Y 1 = 0.5 x 2 + x − 7 Y 1 = 0.5 x 2 + x − 7

To solve the quadratic equation x 2 + 5 x − 7 = 4 , x 2 + 5 x − 7 = 4 , we can graph these two equations

Y 1 = x 2 + 5 x − 7 Y 2 = 4 Y 1 = x 2 + 5 x − 7 Y 2 = 4

and find the points of intersection. Recall 2 nd CALC 5:intersection. Do this and find the solutions to the nearest tenth.

To solve the quadratic equation 0.3 x 2 + 2 x − 4 = 2 , 0.3 x 2 + 2 x − 4 = 2 , we can graph these two equations

Y 1 = 0.3 x 2 + 2 x − 4 Y 2 = 2 Y 1 = 0.3 x 2 + 2 x − 4 Y 2 = 2

Beginning with the general form of a quadratic equation, a x 2 + b x + c = 0 , a x 2 + b x + c = 0 , solve for x by using the completing the square method, thus deriving the quadratic formula.

Show that the sum of the two solutions to the quadratic equation is − b a − b a .

A person has a garden that has a length 10 feet longer than the width. Set up a quadratic equation to find the dimensions of the garden if its area is 119 ft. 2 . Solve the quadratic equation to find the length and width.

Abercrombie and Fitch stock had a price given as P = 0.2 t 2 − 5.6 t + 50.2 , P = 0.2 t 2 − 5.6 t + 50.2 , where t t is the time in months from 1999 to 2001. ( t = 1 t = 1 is January 1999). Find the two months in which the price of the stock was $30.

Suppose that an equation is given p = −2 x 2 + 280 x − 1000 , p = −2 x 2 + 280 x − 1000 , where x x represents the number of items sold at an auction and p p is the profit made by the business that ran the auction. How many items sold would make this profit a maximum? Solve this by graphing the expression in your graphing utility and finding the maximum using 2 nd CALC maximum. To obtain a good window for the curve, set x x [0,200] and y y [0,10000].

Real-World Applications

A formula for the normal systolic blood pressure for a man age A , A , measured in mmHg, is given as P = 0.006 A 2 − 0.02 A + 120. P = 0.006 A 2 − 0.02 A + 120. Find the age to the nearest year of a man whose normal blood pressure measures 125 mmHg.

The cost function for a certain company is C = 60 x + 300 C = 60 x + 300 and the revenue is given by R = 100 x − 0.5 x 2 . R = 100 x − 0.5 x 2 . Recall that profit is revenue minus cost. Set up a quadratic equation and find two values of x (production level) that will create a profit of $300.

A falling object travels a distance given by the formula d = 5 t + 16 t 2 d = 5 t + 16 t 2 ft, where t t is measured in seconds. How long will it take for the object to travel 74 ft?

A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of 378 ft 2 . Find the width of the walkway if the garden is 12 ft. wide by 15 ft. long.

An epidemiological study of the spread of a certain influenza strain that hit a small school population found that the total number of students, P P , who contracted the flu t t days after it broke out is given by the model P = − t 2 + 13 t + 130 , P = − t 2 + 13 t + 130 , where 1 ≤ t ≤ 6. 1 ≤ t ≤ 6. Find the day that 160 students had the flu. Recall that the restriction on t t is at most 6.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/2-5-quadratic-equations

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 9: Graphing Quadratic Equations

9.2: graphs of quadratic equations, learning outcomes.

• Graph quadratic equations of the form [latex]y=ax^2+bx+c[/latex]
• Identify important features of the graphs of quadratic equations
• Determine the maximum or minimum value of a quadratic equation
• Parent equation : the simplest form of a general equation
• Parabola : the shape of any quadratic equation
• Vertex : the turning point of a parabola
• Line of symmetry : a line that cuts the graph into two mirror images

Graphing Quadratic Equations Using Tables

The simplest form of a quadratic equation is [latex]y=ax^2[/latex]. This is also referred to as the  parent equation of any quadratic equation. The basic shape of a quadratic equation is a parabola . It has a vertex where the parabola turns and a line of symmetry that runs through the parabola and splits the graph into two mirror images. We discovered all of this in the last section by determining solutions of the equation and plotting the solution points. We can use this technique for any quadratic equation.

Complete a table of values for the equation [latex]y=2x^2[/latex], then graph the equation.

To create a table of values, we can choose any [latex]x[/latex]-values and find the corresponding [latex]y[/latex]-values.

To create the graph, we plot the points and join the dots.

Notice that it is still a parabola. All quadratic equations take the shape of a parabola.

Complete a table of values for the equation [latex]y=-x^2+4x-3[/latex], then graph the equation. State the vertex and axis of symmetry.

To create the graph, we plot the points.

Unfortunately, the points we chose do not show any symmetry or a turning point. However, the graph looks like it will turn to the right of [latex]x=2[/latex], so let’s find a few other points that lie to the right of [latex]x=2[/latex].

Now we have some symmetry and can join the dots to create the graph.

The vertex is at [latex](2, 1)[/latex] and the axis of symmetry is the vertical line [latex]x=2[/latex].

Notice also, that the point [latex](-2, -15)[/latex] has a twin as a mirror image at [latex](6, -15)[/latex].

In the first example, the parabola opens upwards, while in the second example, the parabola opens downwards. This is determined by the value of [latex]a[/latex] in the equation [latex]y=ax^2+bx+c[/latex]. When [latex]a>0[/latex], the parabola opens upwards. When [latex]a<0[/latex], the parabola opens downwards.  Notice that [latex]a\neq0[/latex] because that would turn the quadratic equation [latex]y=ax^2+bx+c[/latex] into a linear equation [latex]y=bx+c[/latex].

Complete a table of values for the equation [latex]y=-x^2+7[/latex], then graph the equation. State the vertex and axis of symmetry.

First notice that [latex]a=-1[/latex] so the parabola will open downwards.

To complete a table of values we can choose any [latex]x[/latex]-values:

From the graph the vertex is at [latex](0, 7)[/latex] and the line of symmetry is the vertical line [latex]x=0[/latex].

Sometimes it can be messy to draw a graph using just solutions. Deciding which [latex]x[/latex]-values to choose can be bothersome. It can also be impossible to determine exactly where the axis of symmetry and vertex lie if they do not contain integer values. That’s why we use other features of the graph to help us.  For example, it would be helpful to know exactly where the vertex and axis of symmetry lie. Or, where the graph crosses the axes. So, let’s discover how to determine such features.

Features of Parabolas

Intercepts: the [latex]y[/latex]-intercept.

The [latex]y[/latex]-intercept of any graph is found by setting [latex]x=0[/latex] in the equation of the graph and solving for [latex]y[/latex]. For a parabola with equation [latex]y=ax^2+bx+c[/latex], setting [latex]x=0[/latex] results in [latex]y=c[/latex]. Consequently, the [latex]y[/latex]-intercept of any parabola is always the point [latex](0, c)[/latex].

Determine the [latex]y[/latex]-intercept of the graph with equation:

1. [latex]y=4x^2-3x+6[/latex]

2. [latex]y=-2x^2-7[/latex]

3. [latex]y=x^2+5x[/latex]

1. Since [latex]c=6[/latex], the [latex]y[/latex]-intercept is the point [latex](0, 6)[/latex].

2. Since [latex]c=-7[/latex], the [latex]y[/latex]-intercept is the point [latex](0, -7)[/latex].

3. Since [latex]c=0[/latex], the [latex]y[/latex]-intercept is the point [latex](0, 0)[/latex].

1. [latex]y=x^2-4x+1[/latex]

2. [latex]y=-2x^2-3[/latex]

3. [latex]y=x^2-6x[/latex]

• [latex](0, 1)[/latex]
• [latex](0, -3)[/latex]
• [latex](0, 0)[/latex]

Intercepts: The [latex]x[/latex]-Intercepts

The [latex]x[/latex]-intercepts of a parabola occur where the parabola crosses the [latex]x[/latex]-axis (figure 1). Specifically, this is where [latex]y=0[/latex]. So to find the [latex]x[/latex]-intercepts of a parabola, we must solve the equation [latex]ax^2+bx+c=0[/latex].

Figure 1. [latex]x[/latex]-intercepts

Provided this quadratic equation factors, we can solve it using the zero-factor property.  If the equation does not factor, there are alternative ways of solving it that will be taught in the next course.

Find the [latex]x[/latex]-intercepts for the graph of [latex]y={x}^{2}-x-6[/latex].

The [latex]x[/latex]-intercepts are found by solving the equation [latex]x^2 - x - 6 = 0[/latex].

The [latex]x[/latex]-intercepts are [latex]\left(3, 0 \right)[/latex] and [latex] \left( -2, 0 \right) [/latex].

Find the [latex]x[/latex]-intercepts for the graph of [latex]y={x}^{2}-3x+2[/latex].

The graph has two [latex]x[/latex]-intercepts at [latex](1, 0)[/latex] and [latex](2, 0)[/latex]

Find the [latex]x[/latex]-intercepts for the graph of [latex]y={x}^{2}-6x+9[/latex].

The graph has one [latex]x[/latex]-intercept at [latex](3, 0)[/latex].

Parabolas whose equations factor have [latex]x[/latex]-intercepts. But not all parabolas have [latex]x[/latex]-intercepts. Consider the parabolas in figure 2:

Figure 2. Parabolas with 2, 1, or 0 [latex]x[/latex]-intercepts.

Parabolas can have two [latex]x[/latex]-intercepts, one [latex]x[/latex]-intercept, or no [latex]x[/latex]-intercepts.

Find the [latex]x[/latex]-intercepts of the graph of [latex]y = x^2 + 4[/latex].

To find the [latex]x[/latex]-intercepts, we need to solve the equation [latex]x^2 + 4 = 0[/latex].

However, [latex]x^2 + 4[/latex] does not factor.

We can solve this equation by rewriting it:

[latex]x^2 + 4=0[/latex] can be rewritten as [latex]x^2 = -4 [/latex].

There are no real number values for [latex]x[/latex] that when squared result in [latex]-4[/latex].

The only value that [latex]x[/latex] can be are the imaginary numbers [latex]2i[/latex] and [latex]-2i[/latex] because [latex](2i)^2=4i^2=4(-1)=-4[/latex] and [latex](-2i)^2=4i^2=4(-1)=-4[/latex].

Since [latex]2i[/latex] and [latex]-2i[/latex] are complex numbers, they will not show up on the graph.

This parabola will have no [latex]x[/latex]-intercepts.

If a parabola does not intersect with the [latex]x[/latex]-axis,and therefore has no [latex]x[/latex]-intercepts, there are complex number solutions to the equation [latex]y=ax^2+bx+c=0[/latex]. Such solutions cannot be graphed on the real number line, so will not appear on the graph.

Find the [latex]x[/latex]-intercepts of the graph of [latex]y = 9x^2 + 1[/latex].

The graph has no [latex]x[/latex]-intercepts.

Axis of Symmetry and the Vertex

The axis of symmetry and the vertex are very important features of a parabola so being able to find them will be extremely useful for graphing.

Axis of SYmmetry and vertex

For the graph of the equation [latex]y=ax^2+bx+c[/latex], the axis of symmetry is the vertical line [latex]x=-\frac{b}{2a}[/latex].

The vertex is the point where [latex]x=-\frac{b}{2a}[/latex], paired with the corresponding [latex]y[/latex]-value.

For example, consider the equation [latex]y=2x^2-3x+4[/latex]. To find the axis of symmetry calculate [latex]x=-\frac{b}{2a}=-\frac{-3}{2\cdot 2}=\frac{3}{4}[/latex]. The axis of symmetry is the vertical line with equation [latex]x=\frac{3}{4}[/latex].

The axis of symmetry passes through the vertex, so the [latex]x[/latex]-coordinate of the vertex is also [latex]\frac{3}{4}[/latex]. To find the [latex]y[/latex]-coordinate, we substitute [latex]x=\frac{3}{4}[/latex] into the original equation [latex]y=2x^2-3x+4[/latex]:

[latex]\begin{equation}\begin{aligned}y&=2x^2-3x+4 \\ y&=2 {\left (\frac{3}{4}\right )}^{2}-3\cdot\frac{3}{4}+4 \\ y&=2\cdot\frac{9}{16}-\frac{9}{4}+4\\y&=\frac{9}{8}-\frac{18}{8}+\frac{32}{8}\\y&=\frac{23}{8}\end{aligned}\end{equation}[/latex]

The vertex is at the point [latex]\left(\dfrac{3}{4},\dfrac{23}{8}\right)[/latex]. This is verified by the graph in figure 3:

Figure 3. Graph of [latex]y=2x^2-3x+4[/latex]

Find the axis of symmetry and the vertex of the graph with equation [latex]y=-3x^2+x-2[/latex].

Axis:  [latex]x=-\frac{b}{2a}=-\frac{1}{2\cdot (-3)}=-\frac{1}{-6}=\frac{1}{6}[/latex]

Vertex: [latex]x=\frac{1}{6}[/latex], so

[latex]\begin{equation}\begin{aligned}y&=-3x^2+x-2 \\ y&=-3{\left (\frac{1}{6}\right )}^{2}+\frac{1}{6}-2 \\ y&=-\frac{3}{1}\frac{1}{36}+\frac{1}{6}-2 \\ y&=-\frac{1}{12}+\frac{1}{6}-2 \\ y&=\frac{-1+2-24}{12} \\ &y=-\frac{23}{12}\end{aligned}\end{equation}[/latex]

Find the axis of symmetry and the vertex of the graph of the equation [latex]y=2x^2+2x-4[/latex].

Axis: [latex]x=\frac{1}{2}[/latex]

Vertex: [latex]\left (\frac{1}{2}, -\frac{9}{2}\right )[/latex]

Putting it all Together

We have learned some important things about the graphs of quadratic equations that will make it easier for us to create a graph.  These features of a parabola are summarized below:

Graphs of Quadratic Functions

For [latex] \displaystyle y=a{{x}^{2}}+bx+c[/latex], where [latex]a, b[/latex] and [latex]c[/latex] are real numbers, and [latex]a\neq0[/latex],

• The parabola opens upward if [latex]a > 0[/latex] and downward if [latex]a < 0[/latex].
• The [latex]y[/latex]-intercept of the parabola occurs at the point [latex](0,c)[/latex].
• The [latex]x[/latex]-intercepts are found by solving the equation [latex]ax^2+bx+c=0[/latex]. The [latex]y[/latex]-coordinate is zero. There may be 0, 1, or 2 [latex]x[/latex]-intercepts.
• The axis of symmetry is the vertical line [latex]x=\frac{-b}{2a}[/latex].
• The vertex has an [latex]x[/latex]-coordinate of [latex]x=\dfrac{-b}{2a}[/latex]. The [latex]y[/latex]-coordinate is found by substituting this [latex]x[/latex]-value into the equation and solving for [latex]y[/latex].

We can use the properties of parabolas to help us graph a quadratic equation of the form [latex]y=ax^2+bx+c[/latex] without having to calculate an exhaustive table of values.

Graph [latex]y=−2x^{2}+3x–3[/latex].

Let’s start by considering the features of a parabola.

[latex]a=-2[/latex] so the parabola opens downwards.

Since [latex]|a|>1[/latex] the graph will be narrower than the graph of [latex]y=x^2[/latex].

[latex]y[/latex]-intercept :

Since [latex]c=-3[/latex], the [latex]y[/latex]-intercept will be [latex](0, -3)[/latex].

Axis of symmetry:

[latex]x=\frac{-b}{2a}=\frac{-3}{2\cdot (-2)}=\frac{3}{4}[/latex].

[latex]x=\frac{3}{4}[/latex], so [latex]y=−2x^{2}+3x–3=-2{\left (\frac{3}{4}\right )}^{2}+3\cdot \frac{3}{4}-3=-2\cdot \frac{9}{16}+\frac{9}{4}-3=\frac{-9}{8}+\frac{9}{4}-3=\frac{-9+18-24}{8}=\frac{-15}{8}[/latex].  The vertex is the point [latex]\left (\frac{3}{4}, -\frac{15}{8}\right )[/latex].

[latex]x[/latex]-intercepts : 

[latex]−2x^{2}+3x–3[/latex] does not factor, so we cannot find the [latex]x[/latex]-intercepts .

Let’s graph everything we have:

This twin has the same [latex]y[/latex]-value of [latex]-3[/latex]. To find the [latex]x[/latex]-value, move the same number of units past the axis of symmetry to the right.

The point [latex](0, -3)[/latex] is [latex]\frac{3}{4}[/latex] of a unit to the left of the axis, so its twin is [latex]\frac{3}{4}[/latex] of a unit to the right of the axis at [latex]\left (\frac{3}{2}, -3\right )[/latex].

From the information we have found so far, we have the turning point and direction of the graph. Now let’s find some solutions and use their twins to plot more points.

Finally connect the points as best you can using a smooth curve.

Determine the maximum value of [latex]y[/latex]: [latex]y=-4x^2-4x+3[/latex]

Since the graph is a parabola that opens downwards, the maximum value will occur at the vertex.

Find the vertex:  [latex]x=\frac{-b}{2a}=\frac{4}{2\cdot (-4)}=\frac{-1}{2}[/latex]

Then find the [latex]y[/latex]-value:

[latex]y=-4x^2-4x+3\\y=-4{\left (\frac{-1}{2}\right)}^{2}-4\left (\frac{-1}{2}\right )+3\\y=\frac{-4}{1}\cdot\frac{1}{4}+2+3\\y=-1+2+3\\y=4[/latex]

The maximum value is [latex]y=4[/latex].

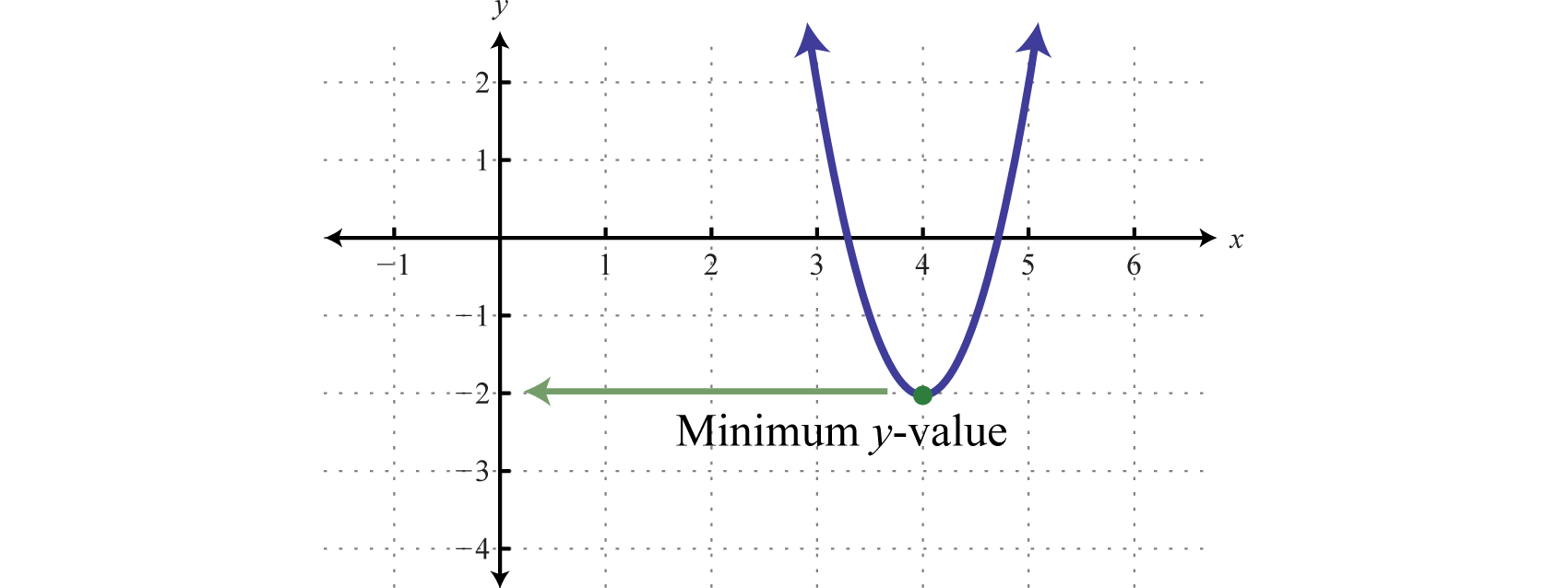
Determine the minimum value of [latex]y[/latex]:  [latex]y=x^2-8x-4[/latex]

The minimum value is [latex]-20[/latex]

• 9.2: Graphs of Quadratic Equations. Authored by : Hazel McKenna . Provided by : Utah Valley University. License : CC BY: Attribution
• All graphs created using desmos graphing calculator. Authored by : Hazel McKenna. Provided by : Utah Valley University. License : CC BY: Attribution

Privacy Policy

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Graph a Quadratic Equation

Last Updated: February 16, 2023 Fact Checked

This article was co-authored by Jake Adams . Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University. There are 18 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 522,423 times.

• For example, two standard form quadratic equations are f(x) = x 2 + 2x + 1 and f(x) = 9x 2 + 10x -8.
• Two vertex form equations are f(x) = 9(x - 4) 2 + 18 and -3(x - 5) 2 + 1
• To graph either of these types of equations, we need to first find the vertex of the parabola, which is the central point (h,k) at the "tip" of the curve. The coordinates of the vertex in standard form are given by: h = -b/2a and k = f(h), while in vertex form, h and k are specified in the equation.

• For example, for the standard form equation f(x) = 2x 2 +16x + 39, we have a = 2, b = 16, and c = 39.
• For the vertex form equation f(x) = 4(x - 5) 2 + 12, we have a = 4, h = 5, and k = 12. [6] X Research source

• In our standard form example (f(x) = 2x 2 +16x + 39), h = -b/2a = -16/2(2). Solving, we find that h = -4 .
• In our vertex form example (f(x) = 4(x - 5) 2 + 12), we know h = 5 without doing any math.

• k = 2(-4) 2 + 16(-4) + 39.
• k = 2(16) - 64 + 39.
• k = 32 - 64 + 39 = 7
• In our vertex form example, again, we know the value of k (which is 12) without having to do any math.

• In our standard form example, our vertex will be at (-4,7). So, our parabola will peak 4 spaces to the left of 0 and 7 spaces above (0,0). We should plot this point on our graph, being sure to label coordinates.
• In our vertex form example, our vertex is at (5,12). We should plot a point 5 spaces to the right and 12 spaces above (0,0).

• In the case of our standard form example, the axis is a line parallel to the y-axis and passing through the point (-4, 7). Though it's not part of the parabola itself, lightly marking this line on your graph can eventually help you see how the parabola curves symmetrically.

• For our standard form example (f(x) = 2x 2 +16x + 39), we know we have a parabola opening upwards because, in our equation, a = 2 (positive).
• For our vertex form example (f(x) = 4(x - 5) 2 + 12), we know we have also have a parabola opening upwards because a = 4 (positive).

• f(x) = 4(x - 12) 2 - 4
• 0 = 4(x - 12) 2 - 4
• 4 = 4(x - 12) 2
• 1 = (x - 12) 2
• SqRt(1) = (x - 12)
• +/- 1 = x -12. x = 11 and 13 are the parabola's x-intercepts.
• x 2 + 2x + 1
• = (x + 1)(x + 1)
• In this case, your only x intercept is -1 because setting x equal to -1 will make either of the factored terms in parentheses equal 0.
• -5x 2 + 1x + 10 gets plugged into the quadratic formula as follows:
• x = (-1 +/- SqRt(1 2 - 4(-5)(10)))/2(-5)
• x = (-1 +/- SqRt(1 + 200))/-10
• x = (-1 +/- SqRt(201))/-10
• x = (-1 +/- 14.18)/-10
• x = (13.18/-10) and (-15.18/-10). The parabola's x intercepts are at approximately x = -1.318 and 1.518
• Our previous standard form example, 2x 2 + 16x + 39 gets plugged into the quadratic formula as follows:
• x = (-16 +/- SqRt(16 2 - 4(2)(39)))/2(2)
• x = (-16 +/- SqRt(256 - 312))/4
• x = (-16 +/- SqRt(-56)/-10
• Because finding the square root of a negative number is impossible, we know that no x intercepts exist for this particular parabola.

• f(x) = 2x 2 + 16x + 39
• f(x) = 2(0) 2 + 16(0) + 39
• f(x) = 39. The parabola's y intercept is at y = 39. As noted above, the y intercept is at y = c.
• f(x) = 4(x - 5) 2 + 12
• f(x) = 4(0 - 5) 2 + 12
• f(x) = 4(-5) 2 + 12
• f(x) = 4(25) + 12
• f(x) = 112. The parabola's y intercept is at y = 112.

• Let's find the y values for the following x values: 0, 1, -2, and -3.
• For 0: f(x) = (0) 2 + 2(0) + 1 = 1. Our point is (0,1).
• For 1: f(x) = (1) 2 + 2(1) + 1 = 4. Our point is (1,4).
• For -2: f(x) = (-2) 2 + 2(-2) + 1 = 1. Our point is (-2,1).
• For -3: f(x) = (-3) 2 + 2(-3) + 1 = 4. Our point is (-3,4).
• Plot these points to the graph and draw your U-shaped curve. Note that the parabola is perfectly symmetrical - when your points on one side of the parabola lie on whole numbers, you can usually save yourself some work by simply reflecting a given point across the parabola's axis of symmetry to find the corresponding point on the other side of the parabola.

Expert Q&A

• Note that in f(x) = ax 2 + bx + c, if b or c equal zero, those numbers disappear. For example, 12x 2 + 0x + 6 becomes 12x 2 + 6 because 0x is 0. Thanks Helpful 17 Not Helpful 15
• Round numbers or use fractions as your algebra teacher tells you to. This will help you graph your quadratic equations properly. Thanks Helpful 10 Not Helpful 14

You Might Also Like

• ↑ Jake Adams. Academic Tutor & Test Prep Specialist. Expert Interview. 20 May 2020.
• ↑ https://math.libretexts.org/Bookshelves/Algebra/Map%3A_College_Algebra_(OpenStax)/05%3A_Polynomial_and_Rational_Functions/502%3A_Quadratic_Functions
• ↑ https://www.mathsisfun.com/algebra/quadratic-equation.html
• ↑ https://mathbitsnotebook.com/Algebra1/Quadratics/QDVertexForm.html
• ↑ https://www.khanacademy.org/test-prep/sat/x0a8c2e5f:untitled-652/x0a8c2e5f:passport-to-advanced-math-lessons-by-skill/a/gtp--sat-math--article--solving-quadratic-equations--lesson
• ↑ https://www.cuemath.com/vertex-formula/
• ↑ https://www.mathsisfun.com/algebra/quadratic-equation-graphing.html
• ↑ https://www.khanacademy.org/math/algebra/quadratics/vertex-form-alg1/v/graphing-a-parabola-in-vertex-form
• ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut34_quadfun.htm
• ↑ https://www.khanacademy.org/math/algebra/quadratics/quad-standard-form-alg1/v/graphing-a-parabola-using-roots-and-vertex
• ↑ https://www.purplemath.com/modules/quadform.htm
• ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratics-using-the-quadratic-formula/a/quadratic-formula-explained-article
• ↑ https://www.csun.edu/~ayk38384/notes/mod11/Parabolas.html
• ↑ http://www.algebra-class.com/graphing-quadratic-equations.html
• http://jwilson.coe.uga.edu/EMT668/EMAT6680.Folders/Barron/unit/Lesson%206/6.html
• http://www.analyzemath.com/quadraticg/quadraticg.htm
• http://www.mathsisfun.com/algebra/quadratic-equation-graphing.html
• http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut34_quadfun.htm

About This Article

To graph a quadratic equation, start by solving for h in vertex form, or taking -b divided by 2 times a in standard form. Then, define or calculate the value of k and plot the point (h, k), which is the vertex of your parabola. In the equation, determine whether a is positive, which means the parabola will open upwards, or negative, which means it will open downwards. To find the x-intercepts, set the function of x equal to 0 which can help you graph the parabola. For tips on finding the y-intercept and other points on the line, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Mar 1, 2017

Did this article help you?

Kishel Melku

May 1, 2018

Featured Articles

Trending Articles

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• ax^2+bx+c=0
• x^2+2x+1=3x-10
• 2x^2+4x-6=0
• How do you calculate a quadratic equation?
• To solve a quadratic equation, use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / (2a).
• What is the quadratic formula?
• The quadratic formula gives solutions to the quadratic equation ax^2+bx+c=0 and is written in the form of x = (-b ± √(b^2 - 4ac)) / (2a)
• Does any quadratic equation have two solutions?
• There can be 0, 1 or 2 solutions to a quadratic equation. If the discriminant is positive there are two solutions, if negative there is no solution, if equlas 0 there is 1 solution.
• What is quadratic equation in math?
• In math, a quadratic equation is a second-order polynomial equation in a single variable. It is written in the form: ax^2 + bx + c = 0 where x is the variable, and a, b, and c are constants, a ≠ 0.
• How do you know if a quadratic equation has two solutions?
• A quadratic equation has two solutions if the discriminant b^2 - 4ac is positive.

quadratic-equation-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 2 Solving quadratics by factorizing (link to previous post) usually works just fine. But what if the quadratic equation...

Please add a message.

Message received. Thanks for the feedback.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Quadratic equations and functions
• Quadratic Plotter

Quadratic function plotter

This calculator draws the quadratic function and finds the x and y intercepts , vertex , and focus . For each of these calculations, the calculator will generate a full explanation.

Most popular calculators

• Factoring Polynomials
• Solving equations
• Rationalize Denominator
• Arithmetic sequences

Polynomial Calculators

• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Expand & Simplify
• Generate From Roots

Rational Expressions

• Simplifying
• Multiplication / Division
• Addition / Subtraction

Radical Expressions

Solving equations.

• Quadratic Equations (with steps)
• Polynomial Equations
• Solving Equations - With Steps

Quadratic Equation

• Solving (with steps)
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism

Complex Numbers

• Modulus, inverse, polar form
• Simplify Expression

Systems of equations

• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition

Calculus Calculators

• Limit Calculator
• Derivative Calculator
• Integral Calculator

Sequences & Series

• Arithmetic Sequences
• Geometric Sequences
• Find n th Term

Analytic Geometry

• Distance and Midpoint
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection

Trigonometry

• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex

Statistics and probability

• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression

Financial Calculators

• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator

Other Calculators

• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

About Graphing Quadratic Functions

Quadratic function has the form $ f(x) = ax^2 + bx + c $ where a, b and c are numbers

You can sketch quadratic function in 4 steps. I will explain these steps in following examples.

Sketch the graph of the quadratic function

In this case we have $ a=1, b=2 $ and $c=-3$

STEP 1: Find the vertex.

To find x - coordinate of the vertex we use formula:

So, we substitute $1$ in for $a$ and $2$ in for $b$ to get

To find y - coordinate plug in $x=-1$ into the original equation:

So, the vertex of the parabola is $ {\color{red}{ (-1,-4) }} $

STEP 2: Find the y-intercept.

To find y - intercept plug in $x=0$ into the original equation:

So, the y-intercept of the parabola is $ {\color{blue}{ y = -3 }} $

STEP 3: Find the x-intercept.

To find x - intercept solve quadratic equation $f(x)=0$ in our case we have:

Solutions for this equation are:

( to learn how to solve quadratic equation use quadratic equation solver )

STEP 4: plot the parabola.

Here we have $ a=-1, b=2 $ and $c=-2$

The x-coordinate of the vertex is:

The y-coordinate of the vertex is:

The y-intercept is:

In this case x-intercept doesn't exist since equation $-x^2+2x-2=0$ does not has the solutions (use quadratic equation solver to check ). So, in this case we will plot the graph using only two points

Related Calculators

Was this calculator helpful?

Please tell me how can I make this better.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.4: Quadratic Functions and Their Graphs

• Last updated
• Save as PDF
• Page ID 6271

Learning Objectives

• Graph a parabola.
• Find the intercepts and vertex of a parabola.
• Find the maximum and minimum \(y\)-value.
• Find the vertex of a parabola by completing the square.

The Graph of a Quadratic Function

A quadratic function is a polynomial function of degree \(2\) which can be written in the general form,

\(f(x)=a x^{2}+b x+c\)

Here \(a, b\) and \(c\) represent real numbers where \(a ≠ 0\).The squaring function \(f (x) = x^{2}\) is a quadratic function whose graph follows.

This general curved shape is called a parabola 10 and is shared by the graphs of all quadratic functions. Note that the graph is indeed a function as it passes the vertical line test. Furthermore, the domain of this function consists of the set of all real numbers \((−∞, ∞)\) and the range consists of the set of nonnegative numbers \([0, ∞)\).

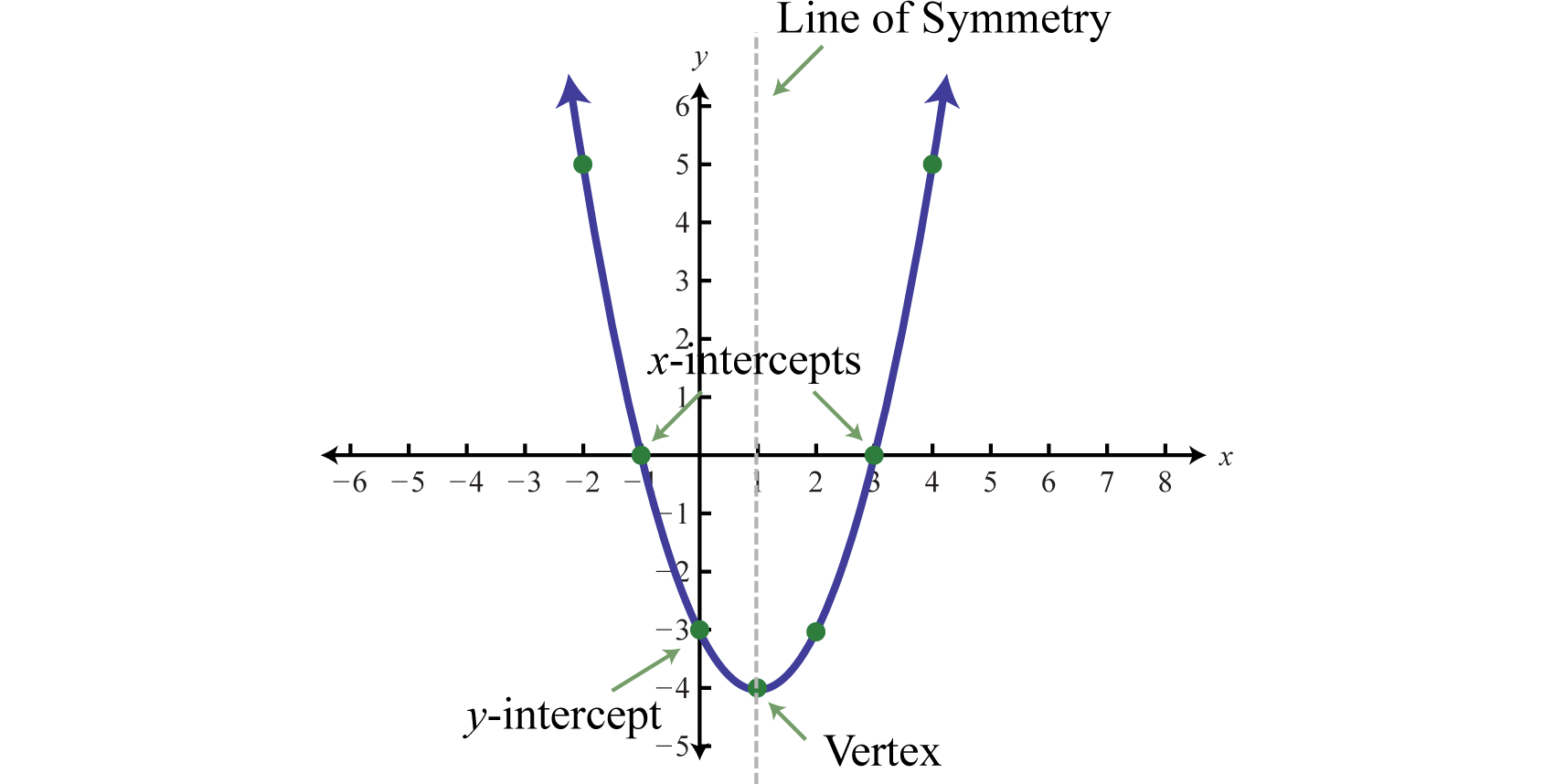
When graphing parabolas, we want to include certain special points in the graph. The \(y\)-intercept is the point where the graph intersects the \(y\)-axis. The \(x\)-intercepts are the points where the graph intersects the \(x\)-axis. The vertex 11 is the point that defines the minimum or maximum of the graph. Lastly, the line of symmetry 12 (also called the axis of symmetry 13 ) is the vertical line through the vertex, about which the parabola is symmetric.

For any parabola, we will find the vertex and \(y\)-intercept. In addition, if the \(x\)-intercepts exist, then we will want to determine those as well. Guessing at the \(x\)-values of these special points is not practical; therefore, we will develop techniques that will facilitate finding them. Many of these techniques will be used extensively as we progress in our study of algebra.

Given a quadratic function \(f (x) = ax^{2} + bx + c\), find the \(y\)-intercept by evaluating the function where \(x = 0\). In general, \(f (0) = a(0)^{2} + b (0) + c = c\), and we have

\(\begin{array}{c}{\color{Cerulean}{y-intercept}} \\ {(0, c)}\end{array}\)

Next, recall that the \(x\)-intercepts, if they exist, can be found by setting \(f (x) = 0\). Doing this, we have \(a^{2} + bx + c = 0\), which has general solutions given by the quadratic formula, \(\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)\).Therefore, the \(x\)-intercepts have this general form:

\(\color{Cerulean}{x-intercepts}\)

\(\left(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}, 0\right)\) and \(\left(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}, 0\right)\)

Using the fact that a parabola is symmetric, we can determine the vertical line of symmetry using the \(x\)-intercepts. To do this, we find the \(x\)-value midway between the \(x\)-intercepts by taking an average as follows:

\(\begin{aligned} x &=\left(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}+\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\right) \div 2 \\ &=\left(\frac{-b-\cancel{\sqrt{b^{2}-4 a c}}-b+\cancel{\sqrt{b^{2}-4 a c}}}{2 a}\right) \div\left(\frac{2}{1}\right) \\ &=\frac{-2 b}{2 a} \cdot \frac{1}{2} \\ &=-\frac{b}{2 a} \end{aligned}\)

Therefore, the line of symmetry is the vertical line \(x = −\frac{b}{2a}\). We can use the line of symmetry to find the the vertex.

\(\begin{array}{c}{\color{Cerulean} { Line\: of\: symmetry }} \quad\quad\quad\color{Cerulean}{Vertex} \\ \quad\quad\quad{x=-\frac{b}{2 a} \quad\quad\quad\quad\left(-\frac{b}{2 a}, f\left(-\frac{b}{2 a}\right)\right)}\end{array}\)

Generally three points determine a parabola. However, in this section we will find five points so that we can get a better approximation of the general shape. The steps for graphing a parabola are outlined in the following example.

Example \(\PageIndex{1}\):

Graph: \(f(x)=-x^{2}-2 x+3\).

Step 1 : Determine the \(y\)-intercept. To do this, set \(x\)=0 and find \(f(0)\).

\(\begin{aligned} f(x) &=-x^{2}-2 x+3 \\ f(0) &=-(\color{OliveGreen}{0}\color{black}{)}^{2}-2(\color{OliveGreen}{0}\color{black}{)}+3 \\ &=3 \end{aligned}\)

The \(y\)-intercept is \((0,3)\).

Step 2 : Determine the \(x\)-intercepts if any. To do this, set \(f(x)=0\) and solve for \(x\).

\(\begin{aligned} f(x)&=-x^{2}-2 x+3 \quad\:\color{Cerulean}{ Set\: f(x)=0. }\\ 0&=-x^{2}-2 x+3 \quad\:\color{Cerulean} { Multiply\: both\: sides\: by\: -1.} \\ 0&=x^{2}+2 x-3 \quad\:\:\:\:\color{Cerulean} { Factor. } \\ 0&=(x+3)(x-1) \:\:\:\color{Cerulean} { Set\: each\: factor\: equal\: to\: zero. }\end{aligned}\)

\(\begin{array}{rl}{x+3=0} & {\text { or } x-1=0} \\ {x=-3} & \quad\quad\quad{x=1}\end{array}\)

Here where \(f (x) = 0\), we obtain two solutions. Hence, there are two \(x\)-intercepts, \((−3, 0)\) and \((1, 0)\).

Step 3 : Determine the vertex. One way to do this is to first use \(x = −\frac{b}{2a}\) to find the \(x\)-value of the vertex and then substitute this value in the function to find the corresponding \(y\)-value. In this example, \(a = −1\) and \(b = −2\).

\(\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)}}{2(\color{OliveGreen}{-1}\color{black}{)}} \\ &=\frac{2}{-2} \\ &=-1 \end{aligned}\)

Substitute \(−1\) into the original function to find the corresponding \(y\)-value.

\(\begin{aligned} f(x) &=-x^{2}-2 x+3 \\ f(\color{OliveGreen}{-1}\color{black}{)} &=-(\color{OliveGreen}{-1}\color{black}{)}^{2}-2(\color{OliveGreen}{-1}\color{black}{)}+3 \\ &=-1+2+3 \\ &=4 \end{aligned}\)

The vertex is \((-1,4)\).

Step 4 : Determine extra points so that we have at least five points to plot. Ensure a good sampling on either side of the line of symmetry. In this example, one other point will suffice. Choose \(x = −2\) and find the corresponding \(y\)-value.

Our fifth point is \((−2, 3)\).

Step 5 : Plot the points and sketch the graph. To recap, the points that we have found are

\(y\)-intercept: \((0,3)\)

\(x\)-intercepts: \((-3,0)\) and \((1,0)\)

Vertex: \((-1,4)\)

Extra point: \((-2,3)\)

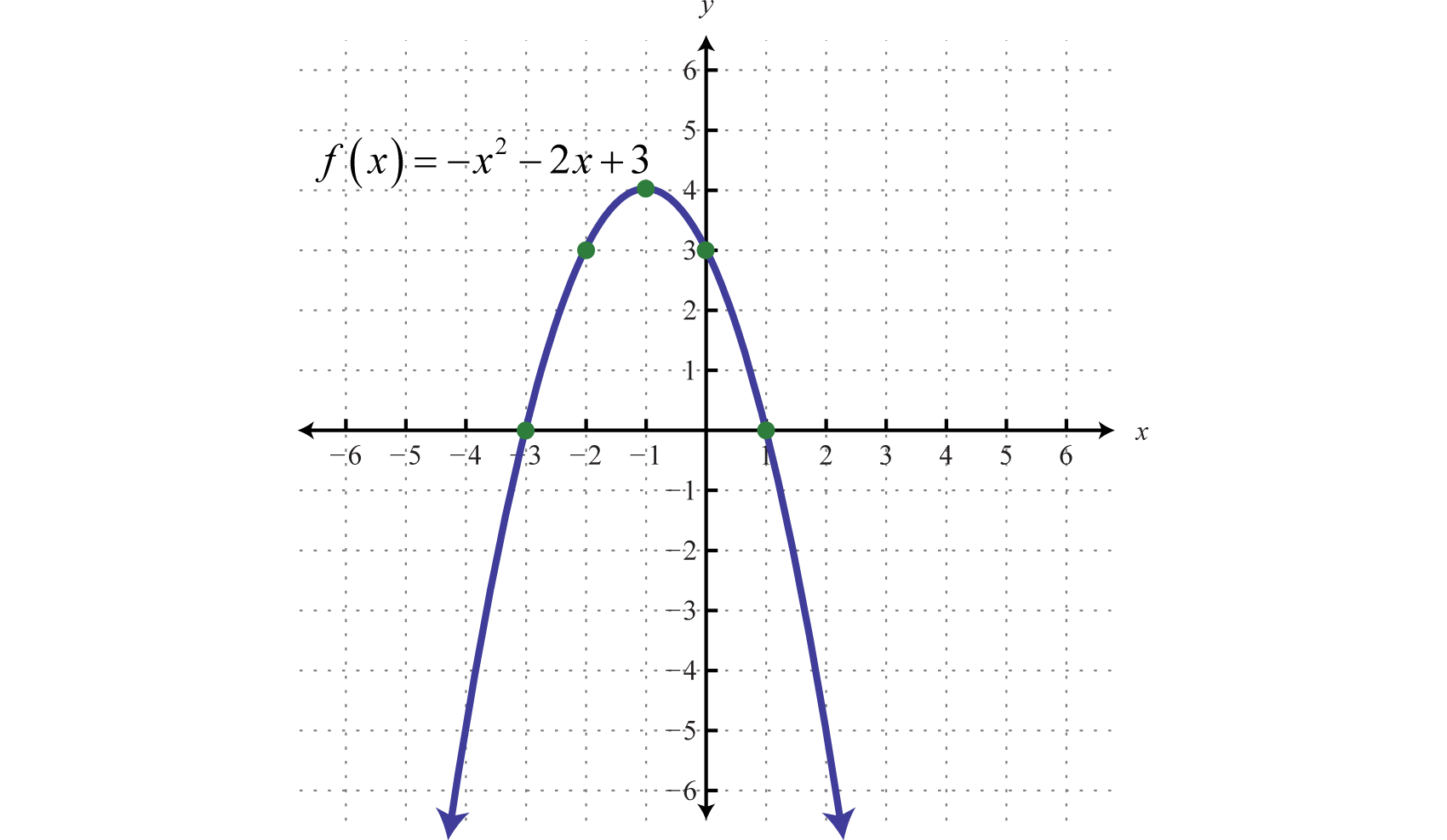
The parabola opens downward. In general, use the leading coefficient to determine if the parabola opens upward or downward. If the leading coefficient is negative, as in the previous example, then the parabola opens downward. If the leading coefficient is positive, then the parabola opens upward.

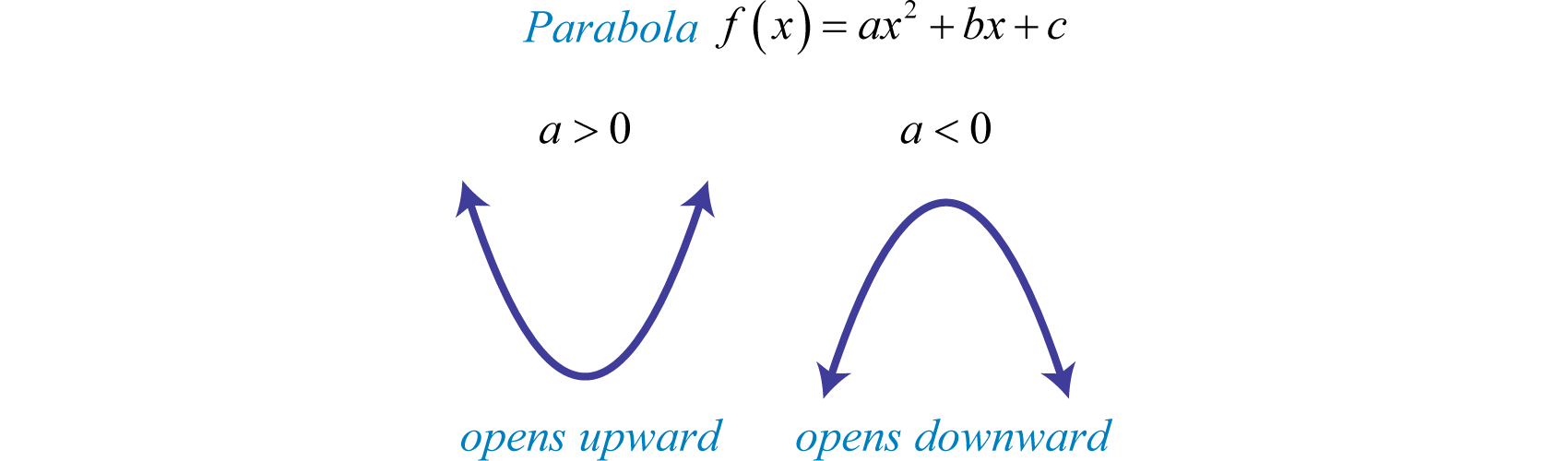
All quadratic functions of the form \(f(x)=a x^{2}+b x+c\) have parabolic graphs with \(y\)-intercept \((0, c)\). However, not all parabolas have \(x\)-intercepts.

Example \(\PageIndex{2}\):

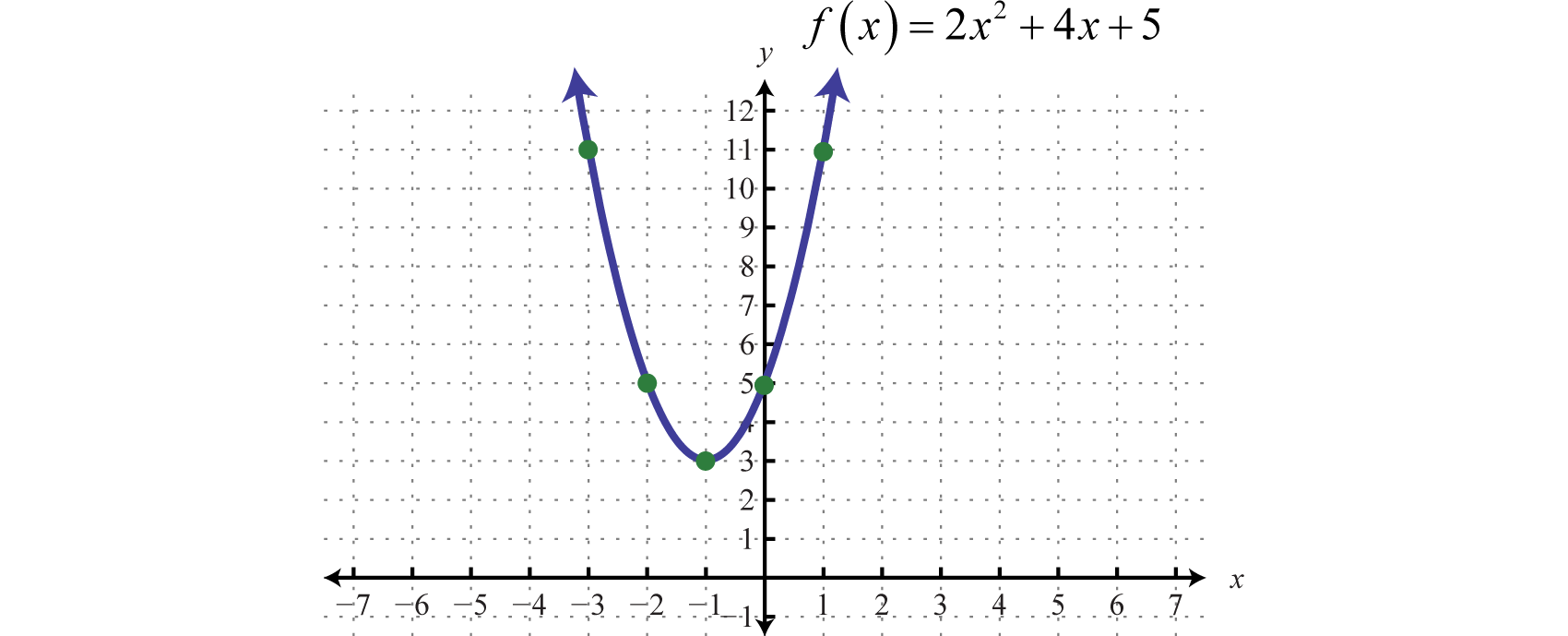
Graph: \(f(x)=2 x^{2}+4 x+5\).

Because the leading coefficient \(2\) is positive, we note that the parabola opens upward. Here \(c = 5\) and the \(y\)-intercept is \((0, 5)\). To find the \(x\)-intercepts, set \(f (x) = 0\).

\(\begin{aligned}f(x)=2 x^{2}+4 x+5 \\ 0=2 x^{2}+4 x+5\end{aligned}\)

In this case, \(a = 2, b = 4\), and \(c = 5\). Use the discriminant to determine the number and type of solutions.

\(\begin{aligned} b^{2}-4 a c &=(4)^{2}-4(2)(5) \\ &=16-40 \\ &=-24 \end{aligned}\)

Since the discriminant is negative, we conclude that there are no real solutions. Because there are no real solutions, there are no \(x\)-intercepts. Next, we determine the \(x\)-value of the vertex.

\(\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{4}\color{black}{)}}{2(\color{OliveGreen}{2}\color{black}{)}} \\ &=\frac{-4}{4} \\ &=-1 \end{aligned}\)

Given that the \(x\)-value of the vertex is \(−1\), substitute \(−1\) into the original equation to find the corresponding \(y\)-value.

\(\begin{aligned} f(x) &=2 x^{2}+4 x+5 \\ f(\color{OliveGreen}{-1}\color{black}{)} &=2(\color{OliveGreen}{-1}\color{black}{)}^{2}+4(\color{OliveGreen}{-1}\color{black}{)}+5 \\ &=2-4+5 \\ &=3 \end{aligned}\)

The vertex is \((−1, 3)\). So far, we have only two points. To determine three more, choose some \(x\)-values on either side of the line of symmetry, \(x = −1\). Here we choose \(x\)-values \(−3, −2\), and \(1\).

To summarize, we have

\(y\)-intercept: \((0,5)\)

\(x\)-intercepts: None

Vertex: \((-1,3)\)

Extra points: \((-3,11), (-2,5), (1,11)\)

Plot the points and sketch the graph.

Example \(\PageIndex{3}\):

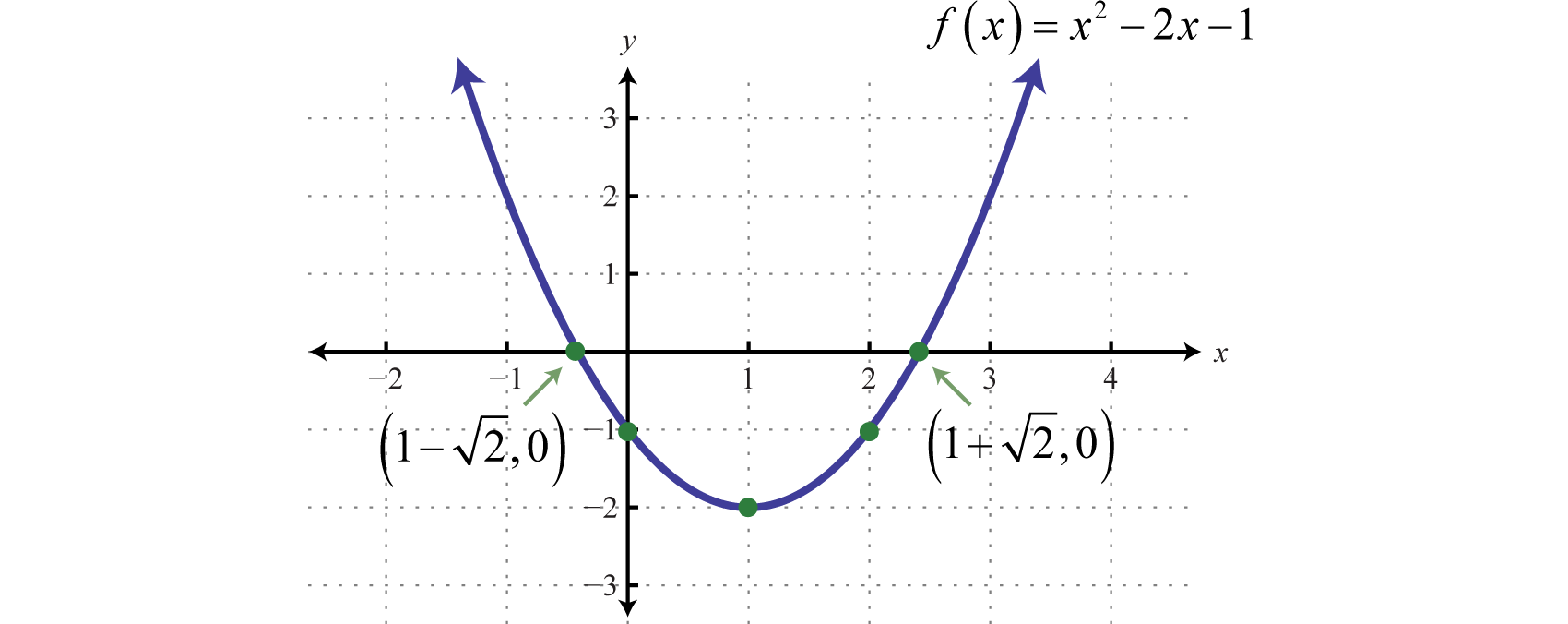
Graph: \(f(x)=x^{2}-2 x-1\).

Since \(a = 1\), the parabola opens upward. Furthermore, \(c = −1\), so the \(y\)-intercept is \((0, −1)\). To find the \(x\)-intercepts, set \(f (x) = 0\).

\(\begin{aligned} f(x) &=x^{2}-2 x-1 \\ 0 &=x^{2}-2 x-1 \end{aligned}\)

In this case, solve using the quadratic formula with \(a = 1, b = −2\), and \(c = −1\).

\(\begin{aligned} x &=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)} \pm \sqrt{(\color{OliveGreen}{-2}\color{black}{)}^{2}-4(\color{OliveGreen}{1}\color{black}{)}(\color{OliveGreen}{-1}\color{black}{)}}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2 \pm \sqrt{8}}{2} \\ &=\frac{2 \pm 2 \sqrt{2}}{2} \\ &= \frac{2(1\pm\sqrt{2})}{2} \\ &=1 \pm \sqrt{2} \end{aligned}\)

Here we obtain two real solutions for \(x\), and thus there are two \(x\)-intercepts:

\(\begin{array}{c}{(1-\sqrt{2}, 0) \text { and }(1+\sqrt{2}, 0)} \quad\color{Cerulean}{Exact\:values} \\ \quad\quad\quad\quad{(-0.41,0) \quad\quad(2.41,0)}\quad\quad\color{Cerulean}{Approximate\:values}\end{array}\)

Approximating the \(x\)-intercepts using a calculator will help us plot the points. However, we will present the exact \(x\)-intercepts on the graph. Next, find the vertex.

\(\begin{aligned} x &=\frac{-b}{2 a} \\ &=\frac{-(\color{OliveGreen}{-2}\color{black}{)}}{2(\color{OliveGreen}{1}\color{black}{)}} \\ &=\frac{2}{2} \\ &=1 \end{aligned}\)

Given that the \(x\)-value of the vertex is \(1\), substitute into the original equation to find the corresponding \(y\)-value.

\(\begin{aligned} y &=x^{2}-2 x-1 \\ &=(\color{OliveGreen}{1}\color{black}{)}^{2}-2(\color{OliveGreen}{1}\color{black}{)}-1 \\ &=1-2-1 \\ &=-2 \end{aligned}\)

The vertex is \((1,-2)\). We need one more point.

\(y\)-intercepts: \((0,1)\)

\(x\)-intercepts: \((1-\sqrt{2}, 0)\) and \((1+\sqrt{2}, 0)\)

Vertex: \((1,-2)\)

Extra point: \((2,-1)\)

Exercise \(\PageIndex{1}\)

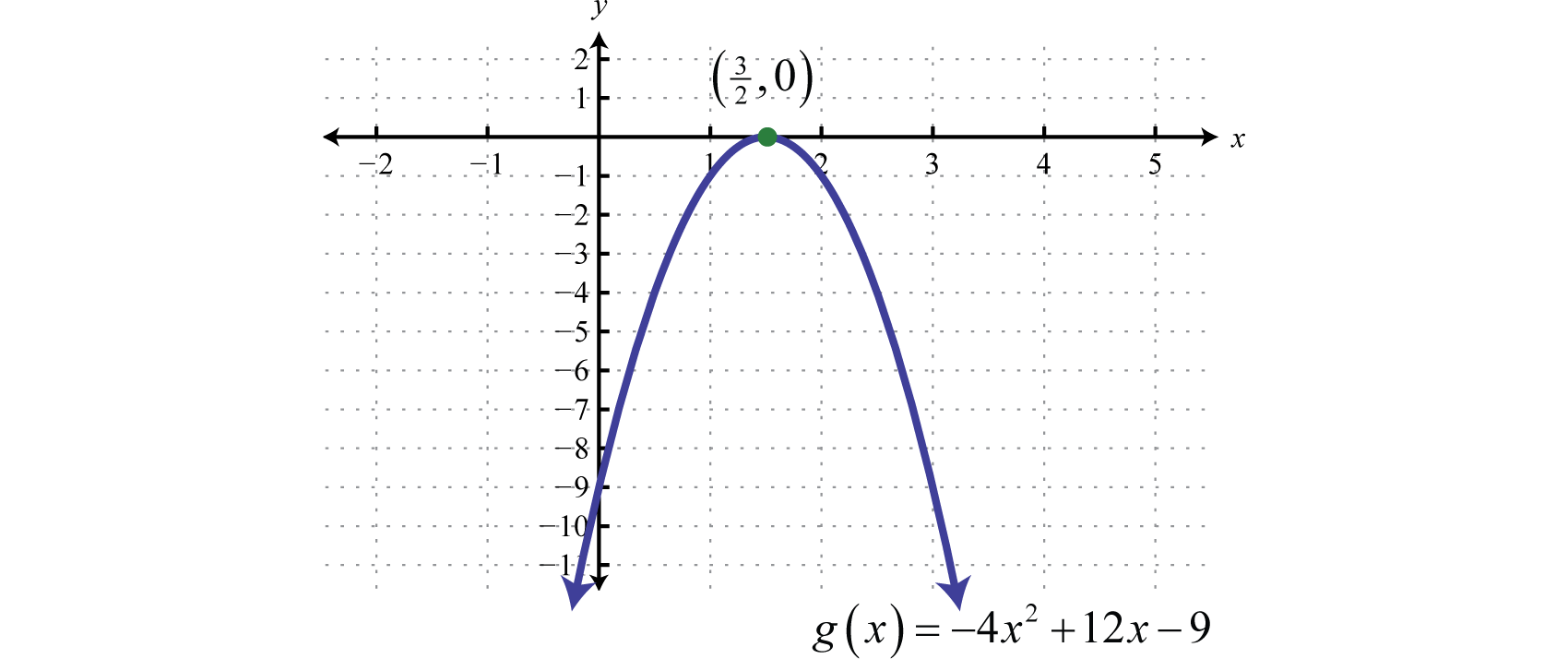
Graph: \(g(x)=-4 x^{2}+12 x-9\).

www.youtube.com/v/tQiDXNhn7ik

Finding the Maximum or Minimum

It is often useful to find the maximum and/or minimum values of functions that model real-life applications. To find these important values given a quadratic function, we use the vertex. If the leading coefficient \(a\) is positive, then the parabola opens upward and there will be a minimum \(y\)-value. If the leading coefficient \(a\) is negative, then the parabola opens downward and there will be a maximum \(y\)-value.

Example \(\PageIndex{4}\):

Determine the maximum or minimum: \(y=-4 x^{2}+24 x-35\).

Since \(a = −4\), we know that the parabola opens downward and there will be a maximum \(y\)-value. To find it, first find the \(x\)-value of the vertex.

\(\begin{aligned} x &=-\frac{b}{2 a} \quad\:\:\:\quad\color{Cerulean}{x-value\:of\:the\:vertex.} \\ &=-\frac{\color{OliveGreen}{24}}{\color{black}{2}(\color{OliveGreen}{-4}\color{black}{)}} \quad\color{Cerulean}{Substitute\:a=-4\:and\:b-24.} \\ &=-\frac{24}{-8} \quad\quad\:\color{Cerulean}{Simplify.}\\ &=3 \end{aligned}\)

The \(x\)-value of the vertex is \(3\). Substitute this value into the original equation to find the corresponding \(y\)-value.

\(\begin{aligned} y &=-4 x^{2}+24 x-35\quad\quad\quad\color{Cerulean}{Substitute\:x=3.} \\ &=-4(3)^{2}+24(3)-35\quad\:\:\color{Cerulean}{Simplify.} \\ &=-36+72-35 \\ &=1 \end{aligned}\)

The vertex is \((3, 1)\). Therefore, the maximum \(y\)-value is \(1\), which occurs where \(x = 3\), as illustrated below:

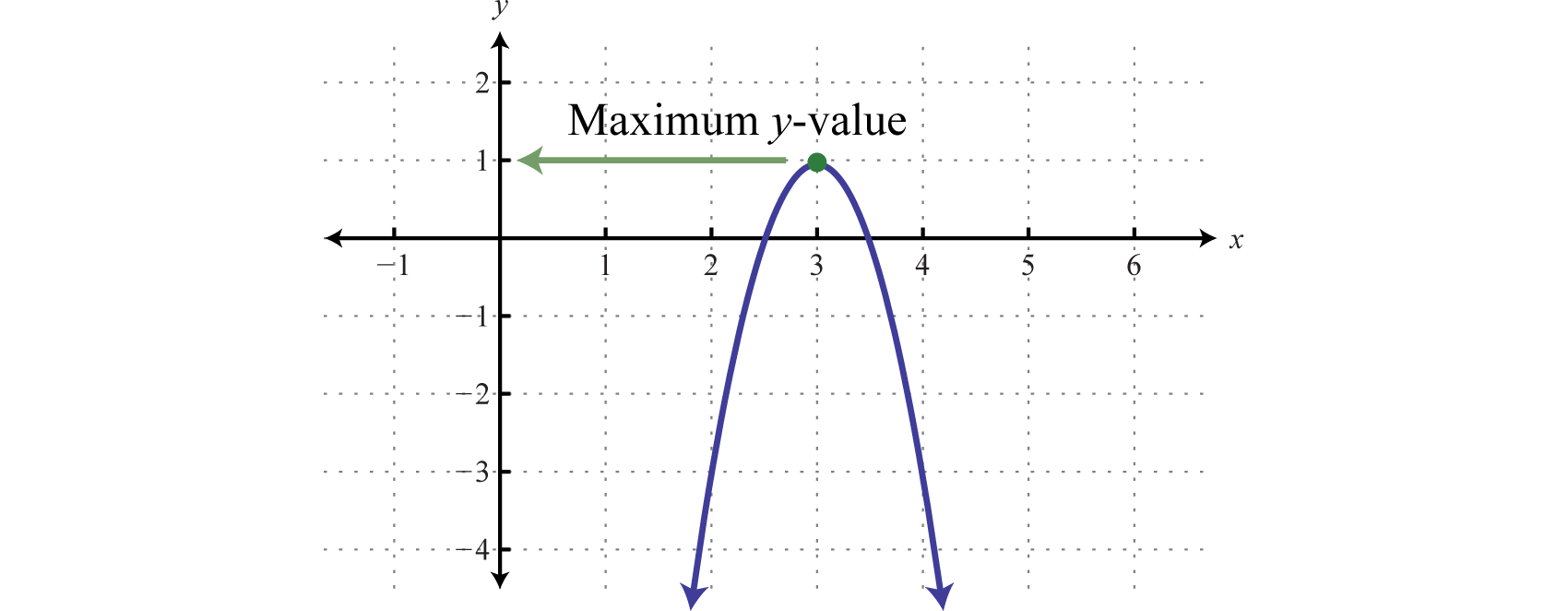
Note : The graph is not required to answer this question.

The maximum is \(1\).

Example \(\PageIndex{5}\):

Determine the maximum or minimum: \(y=4 x^{2}-32 x+62\).

Since \(a = 4\), the parabola opens upward and there is a minimum \(y\)-value. Begin by finding the \(x\)-value of the vertex.

\(\begin{aligned} x &=-\frac{b}{2 a} \\ &=-\frac{\color{OliveGreen}{-32}}{\color{black}{2}(\color{OliveGreen}{4}\color{black}{)}} \quad\color{Cerulean}{Substitute\:a=4\:and\:b=-32.}\\ &=-\frac{-32}{8}\:\:\:\:\color{Cerulean}{Simplify.} \\ &=4 \end{aligned}\)

Substitute \(x = 4\) into the original equation to find the corresponding \(y\)-value.

\(\begin{aligned} y &=4 x^{2}-32 x+62 \\ &=4(\color{OliveGreen}{4}\color{black}{)}^{2}-32(\color{OliveGreen}{4}\color{black}{)}+62 \\ &=64-128+62 \\ &=-2 \end{aligned}\)

The vertex is \((4, −2)\). Therefore, the minimum \(y\)-value of \(−2\) occurs where \(x = 4\), as illustrated below:

The minimum is \(-2\).

Example \(\PageIndex{6}\):

The height in feet of a projectile is given by the function \(h(t)=-16 t^{2}+72 t\), where \(t\) represents the time in seconds after launch. What is the maximum height reached by the projectile?

Here \(a = −16\), and the parabola opens downward. Therefore, the \(y\)-value of the vertex determines the maximum height. Begin by finding the time at which the vertex occurs.

\(t=-\frac{b}{2 a}=-\frac{72}{2(-16)}=\frac{72}{32}=\frac{9}{4}\)

The maximum height will occur in \(\frac{9}{4}\) seconds (or \(2 \frac{1}{4}\) seconds). Substitute this time into the function to determine the maximum height attained.

\(\begin{aligned} h\color{black}{\left(\color{OliveGreen}{\frac{9}{4}}\right)} &=-16\color{black}{\left(\color{OliveGreen}{\frac{9}{4}}\right)^{2}}+72\color{black}{\left(\color{OliveGreen}{\frac{9}{4}}\right)} \\ &=-16\left(\frac{81}{16}\right)+72\left(\frac{9}{4}\right) \\ &=-81+162 \\ &=81 \end{aligned}\)

The maximum height of the projectile is \(81\) feet.

Finding the Vertex by Completing the Square

In this section, we demonstrate an alternate approach for finding the vertex. Any quadratic function \(f (x) = ax^{2} + bx + c\) can be rewritten in vertex form 14 ,

\(f(x)=a(x-h)^{2}+k\)

In this form, the vertex is \((h, k)\). To see that this is the case, consider graphing \(f (x) = (x − 2)^{2} + 3\) using the transformations.

\(\begin{array}{l}{y=x^{2}}\quad\quad\quad\quad\:\quad\color{Cerulean}{Basic\:squaring\:function} \\ {y=(x-2)^{2}}\quad\quad\:\:\:\color{Cerulean}{Horizontal\:shift\:right\:2\:units} \\ {y=(x-2)^{2}+3}\quad\color{Cerulean}{Vertical\:shift\:up\:3\:units}\end{array}\)

Use these translations to sketch the graph,

Here we can see that the vertex is \((2, 3)\).

\(\begin{array}{c}{f(x)=a(x-h)^{2}+k}\\ \color{Cerulean}{\quad\quad\quad\quad\quad\downarrow\:\:\:\quad\downarrow} \\ {f(x)=(x-2)^{2}\:+3}\end{array}\)

When the equation is in this form, we can read the vertex directly from it.

Example \(\PageIndex{7}\):

Determine the vertex: \(f(x)=2(x+3)^{2}-2\).

Rewrite the equation as follows before determining \(h\) and \(k\).

\(\begin{array}{c}{f(x)=\:\:\:a\:(\:x\:-\:h\:)^{2}\:\:+\:\:k} \\ \color{Cerulean}{\quad\quad\quad\quad\quad\quad\:\:\:\:\downarrow\quad\quad\:\:\downarrow} \\{f(x)=2[x-(-3)]^{2}+(-2)}\end{array}\)

Here \(h=-3\) and \(k=-2\).

The vertex is \((-3,-2)\).

Often the equation is not given in vertex form. To obtain this form, complete the square.

Example \(\PageIndex{8}\):

Rewrite in vertex form and determine the vertex: \(f(x)=x^{2}+4 x+9\).

Begin by making room for the constant term that completes the square.

\(\begin{aligned} f(x) &=x^{2}+4 x+9 \\ &=x^{2}+4 x+\_\_\_+9-\_\_\_\end{aligned}\)

The idea is to add and subtract the value that completes the square,\(\left(\frac{b}{2}\right)^{2}\), and then factor. In this case, add and subtract \(\left(\frac{4}{2}\right)^{2}=(2)^{2}=4\).

\(\begin{aligned} f(x) &=x^{2}+4 x+9\quad\quad\quad\quad\:\:\color{Cerulean}{Add\:and\:subtract\:4.} \\ &=x^{2}+4 x\color{Cerulean}{+4}\color{black}{+}9\color{Cerulean}{-4}\quad\color{Cerulean}{Factor.} \\ &=\left(x^{2}+4 x+4\right)+5 \\ &=(x+3)(x+2)+5 \\ &=(x+2)^{2}+5 \end{aligned}\)

Adding and subtracting the same value within an expression does not change it. Doing so is equivalent to adding \(0\). Once the equation is in this form, we can easily determine the vertex.

\(\begin{array}{c}{f(x)=a(x-h)^{2}\:\:+\:\:k}\\\color{Cerulean}{\quad\quad\quad\quad\quad\:\:\:\downarrow\quad\:\:\:\:\:\downarrow} \\ {f(x)=(x-(-2))^{2}+5}\end{array}\)

Here \(h=-2\) and \(k=5\).

The vertex is \((-2,5)\).

If there is a leading coefficient other than \(1\), then we must first factor out the leading coefficient from the first two terms of the trinomial.

Example \(\PageIndex{9}\):

Rewrite in vertex form and determine the vertex: \(f(x)=2 x^{2}-4 x+8\).

Since \(a = 2\), factor this out of the first two terms in order to complete the square. Leave room inside the parentheses to add and subtract the value that completes the square.

\(\begin{aligned} f(x) &=2 x^{2}-4 x+8 \\ &=2\left(x^{2}-2 x\right)+8 \end{aligned}\)

Now use \(−2\) to determine the value that completes the square. In this case, \(\left(\frac{-2}{2}\right)^{2}=(-1)^{2}=1\). Add and subtract \(1\) and factor as follows:

\(\begin{aligned} f(x) &=2 x^{2}-4 x+8 \\ &=2\left(x^{2}-2 x+\_\_\_-\_\_\_\right)+8 \quad\color{Cerulean}{Add\:and\:subtract\:1.} \\ &=2\color{black}{\left(x^{2}-2 x\color{Cerulean}{+1-1}\right)}+8\quad\quad\quad\color{Cerulean}{Factor.} \\ &=2[(x-1)(x-1)-1]+8 \\ &=2\left[(x-1)^{2}-1\right]+8 \quad\quad\quad\quad\:\:\color{Cerulean}{Distribute\:the\:2.} \\ &=2(x-1)^{2}-2+8 \\ &=2(x-1)^{2}+6 \end{aligned}\)

In this form, we can easily determine the vertex.

\(\begin{array}{c}{f(x)=a(x-h)^{2}+k}\\\color{Cerulean}{\quad\quad\quad\quad\quad\:\:\downarrow\quad\:\:\:\downarrow} \\ {f(x)=2(x-1)^{2}+6}\end{array}\)

Here \(h=1\) and \(k=6\).

The vertex is \((1,6)\).

Rewrite in vertex form and determine the vertex: \(f(x)=-2 x^{2}-12 x+3\).

\(f(x)=-2(x+3)^{2}+21\); vertex: \((-3,21)\)

www.youtube.com/v/cmwMn6oZ2dI

Key Takeaways

• The graph of any quadratic function \(f (x) = ax^{2} + bx + c\), where \(a, b\), and \(c\) are real numbers and \(a ≠ 0\), is called a parabola.
• When graphing a parabola always find the vertex and the \(y\)-intercept. If the \(x\)-intercepts exist, find those as well. Also, be sure to find ordered pair solutions on either side of the line of symmetry, \(x = −\frac{ b}{2a}\).
• Use the leading coefficient, \(a\), to determine if a parabola opens upward or downward. If \(a\) is positive, then it opens upward. If \(a\) is negative, then it opens downward.
• The vertex of any parabola has an \(x\)-value equal to \(−\frac{b}{2a}\). After finding the \(x\)-value of the vertex, substitute it into the original equation to find the corresponding \(y\)-value. This \(y\)-value is a maximum if the parabola opens downward, and it is a minimum if the parabola opens upward.
• The domain of a parabola opening upward or downward consists of all real numbers. The range is bounded by the \(y\)-value of the vertex.
• An alternate approach to finding the vertex is to rewrite the quadratic function in the form \(f(x)=a(x-h)^{2}+k\). When in this form, the vertex is \((h, k)\) and can be read directly from the equation. To obtain this form, take \(f (x) = ax^{2} + bx + c\) and complete the square.

Exercise \(\PageIndex{3}\)

Does the parabola open upward or downward? Explain.

• \(y=x^{2}-9 x+20\)
• \(y=x^{2}-12 x+32\)
• \(y=-2 x^{2}+5 x+12\)
• \(y=-6 x^{2}+13 x-6\)
• \(y=64-x^{2}\)
• \(y=-3 x+9 x^{2}\)

3. Downward

5. Downward

Exercise \(\PageIndex{4}\)

Determine the \(x\)- and \(y\)-intercepts.

• \(y=x^{2}+4 x-12\)
• \(y=x^{2}-13 x+12\)
• \(y=2 x^{2}+5 x-3\)
• \(y=3 x^{2}-4 x-4\)
• \(y=-5 x^{2}-3 x+2\)
• \(y=-6 x^{2}+11 x-4\)
• \(y=4 x^{2}-27\)
• \(y=9 x^{2}-50\)
• \(y=x^{2}-x+1\)
• \(y=x^{2}-6 x+4\)

1. \(x\)-intercepts: \((-6,0),(2,0)\); \(y\)-intercept: \((0,-12)\)

3. \(x\)-intercepts: \((-3,0),\left(\frac{1}{2}, 0\right)\); \(y\)-intercept: \((0,-3)\)

5. \(x\)-intercepts: \((-1,0),\left(\frac{2}{5}, 0\right)\); \(y\)-intercept: \((0,2)\)

7. \(x\)-intercepts: \(\left(-\frac{3 \sqrt{3}}{2}, 0\right),\left(\frac{3 \sqrt{3}}{2}, 0\right)\); \(y\)-intercept: \((0,-27)\)

9. \(x\)-intercepts: none; \(y\)-intercept: \((0,1)\)

Exercise \(\PageIndex{5}\)

Find the vertex and the line of symmetry.

• \(y=-x^{2}+10 x-34\)
• \(y=-x^{2}-6 x+1\)
• \(y=-4 x^{2}+12 x-7\)
• \(y=-9 x^{2}+6 x+2\)
• \(y=4 x^{2}-1\)
• \(y=x^{2}-16\)

1. Vertex: \((5,-9)\); line of symmetry: \(x=5\)

3. Vertex: \(\left(\frac{3}{2}, 2\right)\); line of symmetry: \(x=\frac{3}{2}\)

5. Vertex: \((0,-1)\); line of symmetry: \(x=0\)

Exercise \(\PageIndex{6}\)

Graph. Find the vertex and the \(y\)-intercept. In addition, find the \(x\)-intercepts if they exist.

• \(f(x)=x^{2}-2 x-8\)
• \(f(x)=x^{2}-4 x-5\)
• \(f(x)=-x^{2}+4 x+12\)
• \(f(x)=-x^{2}-2 x+15\)
• \(f(x)=x^{2}-10 x\)
• \(f(x)=x^{2}+8 x\)
• \(f(x)=x^{2}-9\)
• \(f(x)=x^{2}-25\)
• \(f(x)=1-x^{2}\)
• \(f(x)=4-x^{2}\)
• \(f(x)=x^{2}-2 x+1\)
• \(f(x)=x^{2}+4 x+4\)
• \(f(x)=-4 x^{2}+12 x-9\)
• \(f(x)=-4 x^{2}-4 x+3\)
• \(f(x)=x^{2}-2\)
• \(f(x)=x^{2}-3\)
• \(f(x)=-4 x^{2}+4 x-3\)
• \(f(x)=4 x^{2}+4 x+3\)
• \(f(x)=x^{2}-2 x-2\)
• \(f(x)=x^{2}-6 x+6\)
• \(f(x)=-2 x^{2}+6 x-3\)
• \(f(x)=-4 x^{2}+4 x+1\)
• \(f(x)=x^{2}+3 x+4\)
• \(f(x)=-x^{2}+3 x-4\)
• \(f(x)=-2 x^{2}+3\)
• \(f(x)=-2 x^{2}-1\)
• \(f(x)=2 x^{2}+4 x-3\)
• \(f(x)=3 x^{2}+2 x-2\)

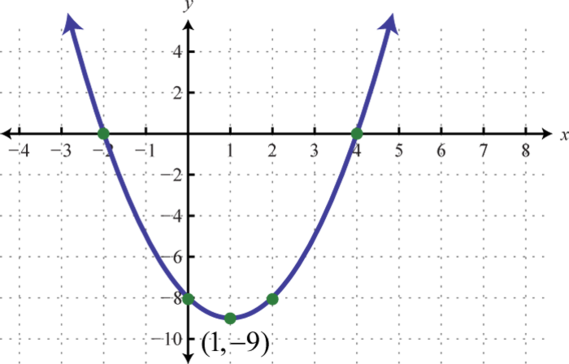
Exercise \(\PageIndex{7}\)

Determine the maximum or minimum \(y\)-value.

• \(y=-x^{2}-4 x+8\)
• \(y=25 x^{2}-10 x+5\)
• \(y=16 x^{2}-24 x+7\)
• \(y=-x^{2}\)
• \(y=1-9 x^{2}\)
• \(y=20 x-10 x^{2}\)
• \(y=12 x+4 x^{2}\)
• \(y=3 x^{2}-4 x-2\)
• \(y=6 x^{2}-8 x+5\)
• \(y=x^{2}-5 x+1\)
• \(y=1-x-x^{2}\)

1. Maximum: \(y = 10\)

3. Minimum: \(y = \frac{4}{5}\)

5. Maximum: \(y = 0\)

7. Maximum: \(y = 10\)

9. Minimum: \(y = −\frac{10}{3}\)

11. Minimum: \(y = −\frac{21}{4}\)

Exercise \(\PageIndex{8}\)

Given the following quadratic functions, determine the domain and range.

• \(f(x)=3 x^{2}+30 x+50\)
• \(f(x)=5 x^{2}-10 x+1\)
• \(g(x)=-2 x^{2}+4 x+1\)
• \(g(x)=-7 x^{2}-14 x-9\)
• \(f(x)=x^{2}+x-1\)
• \(f(x)=-x^{2}+3 x-2\)
• The height in feet reached by a baseball tossed upward at a speed of \(48\) feet per second from the ground is given by the function \(h(t) = −16t^{2} + 48t\), where \(t\) represents the time in seconds after the ball is thrown. What is the baseball’s maximum height and how long does it take to attain that height?
• The height in feet of a projectile launched straight up from a mound is given by the function \(h(t) = −16t^{2} + 96t + 4\), where \(t\) represents seconds after launch. What is the maximum height?
• The profit in dollars generated by producing and selling \(x\) custom lamps is given by the function \(P(x) = −10x^{2} + 800x − 12,000\). What is the maximum profit?
• The profit in dollars generated from producing and selling a particular item is modeled by the formula \(P(x) = 100x − 0.0025x^{2}\), where \(x\) represents the number of units produced and sold. What number of units must be produced and sold to maximize revenue?
• The average number of hits to a radio station Web site is modeled by the formula \(f(x) = 450t^{2} − 3,600t + 8,000\), where \(t\) represents the number of hours since \(8:00\) a.m. At what hour of the day is the number of hits to the Web site at a minimum?
• The value in dollars of a new car is modeled by the formula \(V(t) = 125t^{2} − 3,000t + 22,000\), where \(t\) represents the number of years since it was purchased. Determine the minimum value of the car.
• How many uniforms should be produced to minimize the daily production costs?
• What is the minimum daily production cost?
• The area in square feet of a certain rectangular pen is given by the formula \(A = 14w − w^{2}\), where \(w\) represents the width in feet. Determine the width that produces the maximum area.

1. Domain: \((−∞, ∞)\); range:\([−25, ∞)\)

3. Domain: \((−∞, ∞)\); range: \((−∞, 3]\)

5. Domain: \((−∞, ∞)\); range: \([−\frac{5}{4}, ∞)\)

7. The maximum height of \(36\) feet occurs after \(1.5\) seconds.

9. $\(4,000\)

11. \(12:00\) p.m.

13. (1) \(500\) uniforms (2) $\(5,000\)

Exercise \(\PageIndex{9}\)

Determine the vertex.

• \(y=-(x-5)^{2}+3\)
• \(y=-2(x-1)^{2}+7\)
• \(y=5(x+1)^{2}+6\)
• \(y=3(x+4)^{2}+10\)
• \(y=-5(x+8)^{2}-1\)
• \(y=(x+2)^{2}-5\)

1. \((5, 3)\)

3. \((−1, 6)\)

5. \((−8, −1)\)

Exercise \(\PageIndex{10}\)

Rewrite in vertex form \(y=a(x-h)^{2}+k\) and determine the vertex.

• \(y=x^{2}-14 x+24\)
• \(y=x^{2}-12 x+40\)
• \(y=x^{2}+6 x-1\)
• \(y=2 x^{2}-12 x-3\)
• \(y=3 x^{2}-6 x+5\)
• \(y=-x^{2}+16 x+17\)
• \(y=-x^{2}+10 x\)

1. \(y=(x-7)^{2}-25\); vertex: \((7, -25)\)

3. \(y=(x+2)^{2}-16\); vertex: \((-2, -16)\)

5. \(y=2(x-3)^{2}-21\); vertex: \((3, -21)\)

7. \(y=-(x-8)^{2}+81\); vertex: \((8, 81)\)

Exercise \(\PageIndex{11}\)

• \(f(x)=x^{2}-1\)
• \(f(x)=x^{2}+1\)
• \(f(x)=(x-1)^{2}\)
• \(f(x)=(x+1)^{2}\)
• \(f(x)=(x-4)^{2}-9\)
• \(f(x)=(x-1)^{2}-4\)
• \(f(x)=-2(x+1)^{2}+8\)
• \(f(x)=-3(x+2)^{2}+12\)
• \(f(x)=-5(x-1)^{2}\)
• \(f(x)=-(x+2)^{2}\)
• \(f(x)=-4(x-1)^{2}-2\)
• \(f(x)=9(x+1)^{2}+2\)
• \(f(x)=(x+5)^{2}-15\)
• \(f(x)=2(x-5)^{2}-3\)
• \(f(x)=-2(x-4)^{2}+22\)
• \(f(x)=2(x+3)^{2}-13\)

Exercise \(\PageIndex{12}\)

• Write down your plan for graphing a parabola on an exam. What will you be looking for and how will you present your answer? Share your plan on the discussion board.
• Why is any parabola that opens upward or downward a function? Explain to a classmate how to determine the domain and range.
• Research and discuss ways of finding a quadratic function that has a graph passing through any three given points. Share a list of steps as well as an example of how to do this.

1. Answer may vary

3. Answer may vary

10 The U-shaped graph of any quadratic function defined by \(f (x) = ax^{2} + bx + c\), where \(a, b\), and \(c\) are real numbers and \(a ≠ 0\).

11 The point that defines the minimum or maximum of a parabola.

12 The vertical line through the vertex, \(x = −\frac{b}{2a}\), about which the parabola is symmetric.

13 A term used when referencing the line of symmetry.

14 A quadratic function written in the form \(f(x)=a(x-h)^{2}+k\).