teaching and learning mathematical problem solving

• Open access
• Published: 19 December 2019

Problematizing teaching and learning mathematics as “given” in STEM education

• Yeping Li 1 &
• Alan H. Schoenfeld 2  

International Journal of STEM Education volume  6 , Article number:  44 ( 2019 ) Cite this article

106k Accesses

83 Citations

25 Altmetric

Metrics details

Mathematics is fundamental for many professions, especially science, technology, and engineering. Yet, mathematics is often perceived as difficult and many students leave disciplines in science, technology, engineering, and mathematics (STEM) as a result, closing doors to scientific, engineering, and technological careers. In this editorial, we argue that how mathematics is traditionally viewed as “given” or “fixed” for students’ expected acquisition alienates many students and needs to be problematized. We propose an alternative approach to changes in mathematics education and show how the alternative also applies to STEM education.

Introduction

Mathematics is commonly perceived to be difficult (e.g., Fritz et al. 2019 ). Moreover, many believe “it is ok—not everyone can be good at math” (Rattan et al. 2012 ). With such perceptions, many students stop studying mathematics soon after it is no longer required of them. Giving up learning mathematics may seem acceptable to those who see mathematics as “optional,” but it is deeply problematic for society as a whole. Mathematics is a gateway to many scientific and technological fields. Leaving it limits students’ opportunities to learn a range of important subjects, thus limiting their future job opportunities and depriving society of a potential pool of quantitatively literate citizens. This situation needs to be changed, especially as we prepare students for the continuously increasing demand for quantitative and computational literacy over the twenty-first century (e.g., Committee on STEM Education 2018 ).

The goal of this editorial is to re-frame issues of change in mathematics education, with connections to science, technology, engineering, and mathematics (STEM) education. We are hardly the first to call for such changes; the history of mathematics and philosophy has seen ongoing changes in conceptualization of the discipline, and there have been numerous changes in the past century alone (Schoenfeld 2001 ). Yet changes in practice of how mathematics is viewed, taught, and learned have fallen far short of espoused aspirations. While there has been an increased focus on the processes and practices of mathematics (e.g., problem solving) over the past half century, the vast majority of the emphasis is still on what content should be presented to students. It is thus not surprising that significant progress has not been made.

We propose a two-fold reframing. The first shift is to re-emphasize the nature of mathematics—indeed, all of STEM—as a sense-making activity. Mathematics is typically conceptualized and presented as a body of content to be learned and processes to be engaged in, which can be seen in both the NCTM Standards volumes and the Common Core Standards. Alternatively, we believe that all of the mathematics studied in K-12 can be viewed as the codification of experiences of both making sense and sense making through various practices including problem solving, reasoning, communicating, and mathematical modeling, and that students can and should experience it that way. Indeed, much of the inductive part of mathematics has been lost, and the deductive part is often presented as rote procedures rather than a form of sense making. If we arrange for students to have the right experiences, the formal mathematics can serve to organize and systematize those experiences.

The second shift is suggested by the first, with specific attention to classroom instruction. Whether mathematics or STEM, the main focus of most instruction has been on the content and practices of the discipline, and what the teacher should do in order to make it accessible to students. Instead, we urge that the main focus should be on the student’s experience of the discipline – on the affordances the environment provides the student for disciplinary sense making. We will introduce the Teaching for Robust Understanding (TRU) Framework, which can be used to problematize instruction and guide needed reframing. The first dimension of TRU (The Discipline) focuses on the re-framing discussed above: is the content conceptualized as something rich and connected that can be experienced and codified in meaningful ways? The second dimension (Cognitive Demand) examines opportunities students have to do that kind of sense-making and codification. The third (Equitable Access to Content) examines who has such opportunities: is there equitable access to the core ideas? Dimension 4 (Agency, Ownership, and Identity) asks, do students encounter the discipline in ways that enable them to see themselves as sense makers, building both agency and positive disciplinary identities? Finally, dimension 5 (Formative Assessment) asks, does instruction routinely use formative assessment, allowing student thinking to become public so that instruction can be adjusted accordingly?

We begin with a historical background, briefly discussing different views regarding the nature of mathematics. We then problematize traditional approaches to mathematics teaching and learning. Finally, we discuss possible changes in the context of STEM education.

Knowing the background: the development of conceptions about the nature of mathematics

The scholarly understanding of the nature of mathematics has evolved over its long history (e.g., Devlin 2012 ; Dossey 1992 ). Explicit discussions regarding the nature of mathematics took place among Greek mathematicians from 500 BC to 300 AD (see, https://en.wikipedia.org/wiki/Greek_mathematics ). In contrast to the primarily utilitarian approaches that preceded them, the Greeks pioneered the study of mathematics for its own sake and pursued the development and use of generalized mathematical theories and proofs, especially in geometry and measurement (Boyer 1991 ). Different perspectives about the nature of mathematics were gradually developed during that time. Plato perceived the study of mathematics as pursuing the truth that exists in external world beyond people’s mind. Mathematics was treated as a body of knowledge, in the ideal forms, that exists on its own, which human’s mind may or may not sense. Aristotle, Plato’s student, believed that mathematicians constructed mathematical ideas as a result of the idealization of their experience with objects (Dossey 1992 ). In this perspective, Aristotle emphasized logical reasoning and empirical realization of mathematical objects that are accessible to the human senses. The two schools of thought that evolved from Plato’s and Aristotle’s contrasting conceptions of the nature of mathematics have had important implications for the ensuing development of mathematics as a discipline, and for mathematics education.

Several more schools of thought were developed as mathematicians tackled new problems in mathematics (Dossey 1992 ). Davis and Hersh ( 1980 ) provides an entertaining and informative account of these developments. Three major schools of thought in the early 1900s dealt with paradoxes in the real number system and the theory of sets: (1) logicism, as an outgrowth of the Platonic school, accepts the external existence of mathematics and emphasizes the form rather than the interpretation in a specific setting; (2) intuitionism, as influenced by Aristotle’s ideas, only accepts the mathematics to be developed from the natural numbers forward via “valid” patterns of mental reasoning (not empirical realization in Aristotle’s thought); and (3) formalism, also aligned with Aristotle’s ideas, builds mathematics upon the formal axiomatic structures to free mathematics from contradictions. These three schools of thought are similar in that they view the contents of mathematics as products , but they differ in whether products are viewed as pre-existing or created through experience. The development of these three schools of thought illustrates that the view of mathematics as products has its long history in mathematics.

With the gradual development of school mathematics since 1900s (Stanic and Kilpatrick 1992 ), the conception of the nature of mathematics has increasingly received attention from mathematics educators. Which notion of mathematics mathematics education adopts and uses has a direct and strong impact on the way of school mathematics being presented and approached in education. Although the history of school mathematics is relatively short in comparison with mathematics itself, we can find ample examples about the influence of different views of mathematics on curriculum and classroom instruction in the USA and other education systems (e.g., Dossey et al. 2016 ; Li and Lappan 2014 ; Li, Silver, and Li 2014 ; Stanic and Kilpatrick 1992 ). For instance, the “New Math” movement of 1950s and 1960s used the formalism school of thought as the core of reform efforts. The content was presented in a structural format, using the set theoretic language and conceptions. But the result was not a successful progression toward a school mathematics that is best for students and teachers (e.g., Kline 1973 ). Alternatively, Dossey ( 1992 ), in his review of the nature of mathematics, identified and selected scholars’ works and ideas applicable to both professional mathematicians and mathematics educators (e.g., Davis and Hersh 1980 ; Hersh 1986 ; Tymoczko 1986 ). Those scholars' ideas rested on what professional mathematicians do, not what mathematicians think about what mathematics is. Dossey ( 1992 ) specifically cited Hersh ( 1986 ) to emphasize mathematics is about ideas and should be accepted as a human activity, not strictly governed by any one school of thought.

Devlin ( 2000 ) argued that mathematics is not a single entity but has four different faces: (1) computation, formal reasoning, and problem solving; (2) a way of knowing; (3) a creative medium; and (4) applications. Further, he contended school mathematics typically focuses on the first face, makes some reference to the fourth face, but pays almost no attention to the other two faces. His conception of mathematics assembles ideas from the history of mathematics and observes mathematical activities occurring across different settings.

Our brief review shows that the nature of mathematics can be understood as having different faces, rather than being governed by any single school of thought. At the same time, the ideas of Plato and Aristotle continue to influence the ways that mathematicians, mathematics educators, and the general public perceive mathematics. Despite nearly a half century of process-oriented research (see below), let alone Pólya’s work on problem solving, mathematics is still perceived of largely as products —a body of knowledge as highlighted in the three schools (logicist, intuitionist, formalist) of thought, rather than ideas that call for active thinking and creation. The evolving conceptions about the nature of mathematics in history suggests there is room for us to decide how mathematics can be perceived, rather than being bounded by a pre-occupied notion of mathematics as “given” or “fixed.” Each and every learner can experience mathematics through different practices and “own” mathematics as a human activity.

Problematizing what is important for students to learn in and through mathematics

The evolving conceptions about the nature of mathematics suggest that choices exist when deciding what and how to teach and learn mathematics but they do not specify what and how to make the choice. Decisions require articulating options for conceptions of what is important for students to learn in and through mathematics and evaluating the advantages and drawbacks for the students for each option.

According to Stanic and Kilpatrick ( 1992 ), the history of school mathematics curricula presents two important and real changes over the years: one is at the turn of the twentieth century when school mathematics was reformed as a unified and applied curriculum to accommodate dramatically increased student populations from diverse backgrounds, and the other is the “New Math” movement of the 1950s and 1960s, intended to integrate modern mathematics into school curriculum. The perceived failure of the “New Math” movement led to the “Back to Basics” movement in the 1970s, followed by “Problem Solving” in the 1980s, and then the Curriculum Standards movement in the 1990s and after. The history shows school mathematics curricula have emphasized teaching and learning mathematical knowledge and skills, together with problem solving and some applications of mathematics, a picture that is consistent with what Devlin ( 2000 ) refers to as the 1st face and some reference to the 4th face of mathematics.

Therefore, although there have been reforms in mathematics curriculum and instruction, there are hardly real changes in how mathematics is conceptualized and presented in school education in the USA (Stanic and Kilpatrick 1992 ) and other education systems (e.g., Leung and Li 2010 ; Li and Lappan 2014 ). The dominant conception remains mathematics as products , frequently referring to a body of static knowledge and skills that need to be learned and acquired (Fisher 1990 ). This continues to be largely the case in practice, despite advances in conceptualization (see below).

It should be noted that conceptualizing mathematics as “a body of knowledge and skills” is not wrong, especially with such a long history of knowledge creation and accumulation in mathematics, but it is not adequate for school mathematics nowadays. The set of concepts and procedures, after years of development, exceeds what could be covered in any school curricula. Moreover, this body of knowledge and skills keeps growing, as the product of human intelligence and scholarship in mathematics. Devlin ( 2012 ) pointed out that school mathematics mainly covers what was developed in the Greek mathematics, plus just two further advances from the seventh century: calculus and probability theory. It is no wonder if someone questions the value of learning such a small set of knowledge and skills developed more than a thousand years ago. Meanwhile, this body of knowledge and skills are often abstract, static, and “foreign” to many students and teachers who learned to perceive mathematics as an external entity in existence (Plato’s notion) rather than Aristotelian emphasis on experimentation (Cooney 1987 ). It is thus not surprising for so many students and teachers to claim that mathematics is difficult (e.g., Fritz et al. 2019 ) and “it is ok—not everyone can be good at math” (Rattan et al. 2012 ).

What can be made meaningful should be critically important to those who want to (or need to) learn and teach mathematics. In fact, there is significant evidence that students often try to make sense of mathematics that is “presented” or “given” to them, although they made numerous errors that can be decoded to study their thinking (e.g., Ashlock 2010 ). Indeed, misconceptions are best thought of not as errors that need to be “fixed,” but as plausible abstractions on the basis of what students have learned—i.e., attempts at sense-making (Smith et al. 1993 ). Conceiving mathematics as about “ideas,” we can help students to play, own, experience, and think about some key ideas just like what they do in many other activities, such as game play (Gee 2005 ). Definitions of concepts and formal languages and procedures can be postponed until students are ready to consider why and how they are needed. Mathematics should be taken and accepted as a human activity (Dossey 1992 ), and developing students’ mathematical thinking (about ideas) should be emphasized in learning mathematics itself (Devlin 2012 ) and in STEM (Li et al. 2019a ).

Along with the shift from products to ideas in mathematics, scholars have already focused on how people work with ideas in mathematics. Elaborated in detail by Schoenfeld ( in press ), the revolution began with George Pólya (1887–1985) who had a fundamental interest in having students learn and understand content via problem solving. For Pólya, mathematics was about inquiry, sense making, and understanding how and why mathematical ideas (instead of content as products) fit together the way they do. The call for problem solving in the 1980s in the USA was (at least partially) inspired by Pólya’s ideas after a decade of “back to basics” in the 1970s. It has been recognized since that the practices of mathematics (including problem solving) are every bit as important as the content itself, and the two shouldn’t be separated. In the follow-up standards movement, the content and practices have been the “warp and weave” of the fabric doing mathematics, as articulated in Principles and Standards for School Standards (NCTM 2000 ). There were five content standards and five process standards (i.e., problem solving, reasoning, connecting, communicating, representing). It is widely acknowledged, also in the Common Core State Standards in the USA (CCSSI 2010 ), that both content and processes/practices are essential and they form the base for next steps.

Problematizing how mathematics is taught and learned, with connections to STEM education

How the ways that mathematics is often taught cause concerns.

Conceiving mathematics as a body of facts and procedures to be “mastered” has been long-standing in mathematics education practice, and it often results in students’ learning by rote memorization. For example, Schoenfeld ( 1988 ) provided a detailed account of the disasters of a “well-taught” mathematics course, documenting a 10th-grade geometry class taught by a confident and experienced teacher. The teacher taught and managed his class well, and his students also did well on standardized examinations, which focused on content and procedures. At the same time, however, Schoenfeld pointed out that the students developed counterproductive views of mathematics. Although the students developed some level of proficiency in content and procedures, they gained (or were reinforced in) the kinds of beliefs about mathematics as being fragmented and disconnected. Schoenfeld argued that the course led students to develop a robust and counterproductive set of beliefs about the nature of geometry.

Seeking possible origins about students’ counterproductive beliefs about mathematics from mathematics instruction motivated Schoenfeld’s study (Schoenfeld 1988 ). Such an intuitive motivation is also evident in other studies. Keitel ( 2006 ) compared the lessons of two teachers (T1 and T2) in Germany who taught their classes very differently. T1 regularly taught the class emphasizing routine individual practice and memorization of specific algebraic rules. T1 emphasized the importance of such practices for test taking, and the students followed his instruction. Even when T1 one day introduced a non-routine problem that connects algebra and geometry, the overwhelming emphasis on mastering routines and algorithms seemed to overshadow in dealing such a non-routine problem. In contrast, T2’s teaching emphasized students’ initiatives and collaboration, although T2 also used formal routine tasks. At the end, students in T2’s class reported positively about their experience, enjoyed working together, and appreciated the opportunities of thinking mathematically. Studies by Schoenfeld ( 1988 ) and Keitel ( 2006 ) indicate how students’ experience in mathematics classes influences their perceptions of mathematics and also imply the importance of learning about teachers’ perceptions of mathematics that likely guide their instructional practice (Cooney 1987 ).

Rattan et al. ( 2012 ) found that teachers with different perceptions of mathematics teach differently. Specifically, Rattan et al. looked at these teachers holding an entity (fixed) theory of mathematics intelligence (G1) versus incremental theory (G2). Through their studies, Rattan and colleagues found that G1 teachers more readily judged students to have low ability, comforted students for low mathematical ability, and used “kind” strategies (e.g., assigning less homework) unlikely to promote their engagement with the field than G2 teachers. Students who received comfort-oriented feedback perceived their teachers’ entity theory and low expectations and reported lowered motivation and expectations for their own performance. The results suggest how teachers’ inadequate perceptions of mathematics and beliefs about the nature of students’ mathematical intelligence contributed to low achievement, diminished self-esteem and viewed mathematics is only a set of static facts and procedures. Further, the results suggest that how mathematics is taught influences more than students’ proficiency with mathematics content in a class. Sun ( 2018 ) made a similar argument after synthesizing existing literature and analyzing classroom observation data.

Based on the 2012 US national survey of science and mathematics education conducted by Horizon Research, Banilower et al. ( 2013 ) reported that a vast majority of mathematics teachers, from 81% at the high school level to 90% at the elementary level, believe that students should be given definitions of new vocabulary at the beginning of instruction on a mathematical idea. Also, many teachers believe that they should explain an idea to students before having them consider evidence for it and that hands-on activities should be used primarily to reinforce ideas students have already learned. The report suggests many teachers emphasized pedagogical practices of “give” and “present,” perhaps influenced by conceptions of mathematics that are more Platonic than Aristotelian, similar to what was reported about teachers’ practices more than two decades ago (Cooney 1987 ).

How to change?

Given that the evidence demonstrates a compelling case for changing how mathematics is taught, we turn our attention to suggesting how to realize this transformation. Changing how mathematics is taught and learned is not a new endeavor for both mathematics educators and mathematicians (e.g., Li, Silver, and Li 2014 ; Schoenfeld in press ). For example, the “Moore Method,” developed and used by Robert Lee Moore (a famous topologist) in the early twentieth century, shifted instruction from teacher-centered lecturing to student-centered mathematical development (Coppin et al. 2009 ). In its purest form, students were presented with mathematical definitions and asked to develop and/or prove theorems from them after class, without reading mathematics books or using other resources. When students returned to the class, they were asked to prove a theorem. As a result, students developed the mathematics themselves, instead of the instructor presenting the proofs and doing the mathematics for students. The method has had its own success in producing many great mathematicians; however, the high-pressure environment also drowned many students who might have been successful otherwise (Schoenfeld in press ).

Although the “Moore Method” was used primarily in advanced mathematics courses at the post-secondary level, it illustrates how a different conception of mathematics led to a different instructional approach in which students developed mathematics. However, it might be the opposite end of a spectrum, in comparison to approaches that present mathematics to students in accommodating and easy-to-digest ways that can be as much easy as possible. Neither extreme is a good option for K-12 students. Again, it becomes important for us to consider options that can support the value of learning mathematics.

Our discussion in the previous section highlights the importance of taking mathematics as a human activity, ensuring it is meaningful to students, and developing students’ mathematical thinking about ideas, rather than simply absorbing a set of static and disconnected knowledge and skills. We call for a shift in teaching mathematics based on Platonic conceptions to approaches based on more of Aristotelian conceptions. In essence, Plato emphasized ideal forms of mathematical objects, perhaps inaccessible through people’s sense making efforts. As a result, learners lack ownership of the ideal forms of mathematical objects, because mathematical objects cannot and should not be created by human reasoning. In contrast, Aristotle emphasized that mathematical objects are developed through logic reasoning and empirical realization. In other words, mathematical objects exist only when they can be sensed and verified by people's efforts. This differs from Plato’s passive perspective, highlights human ownership of mathematical ideas and encourages people to make mathematics make sense, termed as making sense by McCallum ( 2018 ). Aristotelian conceptions view mathematics as objects that learners can actively develop and structure as mathematically meaningful, which is more in line with what research mathematicians do. McCallum ( 2018 ) argued that both sense-making and making-sense stances are needed for a complete view of mathematics and learning, recognizing that not attending to both stances carries risks. “Just as it is a risk of the sense-making stance that the mathematics gets ignored, it is a risk of the making-sense stance that the sense-maker gets ignored.” (McCallum 2018 ).

In addition, there is the issue of personal identity: if students come to avoid mathematics because they are uncomfortable with it (in fact, mathematics anxiety has become a widespread problem for all ages across the globe, see Luttenberger et al. 2018 ) then mathematics instruction has failed them, regardless of test scores.

In the following, we discuss sense-making and making-sense stances first with specific examples from mathematics. Then, we discuss connections to STEM education.

Sense making is much more than the acquisition of knowledge and skills

Sense making has long been emphasized in mathematics education community. William A. Brownell is a well-known, early 20 th century scholar who advocated the value of sense making in the learning of mathematics. For example, Brownell ( 1945 ) discussed how arithmetic can and should be taught and learned not only as procedures, but also as a meaningful system of thinking. He shared many examples like the following division,

Brownell suggested to ask questions: what does the 5 of 576 mean? Why must 57 be the first partial dividend? Do you actually divide 8 into 57, or into 57…’s? etc., instead of simply letting students memorize how to carry out the procedure. What Brownell advocated has been commonly accepted and emphasized in mathematics education nowadays as sense making (e.g., Schoenfeld 1992 ).

There can be different ways of sense making of the same computation. As an example, the sense making process for the above long division can come out with mental math as: I am looking to see how close I can get to 570 with multiples of 80; 7 multiples of 80 gives me 560, which is close. Of course, given base 10 notation, that’s the same as 8 multiples of 70, which is why the 7 goes over the 57. And when I subtract 560, there are 16 left over, so that’s another 2 8 s. Such a sense-making process also works, as finding the answer (quotient, k ) of 576 ÷ 8 is the same operation as to find k that satisfies 576 = k × 8. In mathematics, division and multiplication are alternate but equivalent ways of doing the same operation.

To help students build numerical reasoning and make sense of computations, many teachers use number talks in their classrooms for students to practice and share these mental math and computation strategies (e.g., Parrish 2011 ). In fact, new terms are being created and used in mathematics education about sense making, such as number sense (e.g., Sowder 1992 ) and symbol sense (Arcavi, 1994 ). Some instructional programs, such as Cognitively Guided Instruction (see, e.g., Carpenter et al., 1997 , 1998 ), make sense making the core of instructional activities. We argue that such activities should be more widely adopted.

Making sense makes the other side of mathematical practice visible, and values idea development and ownership

The making-sense stance, as termed by McCallum ( 2018 ), is not commonly practiced as it is pertinent to expert mathematician’s practices. Where sense making (as discussed previously) emphasizes the process of making sense of what is being learned, making sense emphasizes the process of making mathematics make sense. Making sense highlights the importance for students to experience mathematics through creating, designing, developing, and connecting mathematical ideas. As an example, for the above division computation, 8 \( \overline{\Big)576\ } \) , students may wonder why the division procedure is performed from left to right, which is different from the other operations (addition, subtraction, and multiplication) that are all performed from right to left. In fact, students can be encouraged to explore if the division can also be performed from right to left (i.e., starting from the one’s place). They may discover, with possible support from the teacher, that the division can be done in this way. However, once the division is moved to the high-value places, it will require the process to go back down to the low-value places for completion. In other words, the division process starting from the low-value place would require repeated processes of returning to the low-value places; as a result, it is inefficient. As mathematical procedure is designed to improve efficiency, the division procedure is thus set to be carried out from the high-value place to low-value place (i.e., from left to right). Students who work this out experience mathematics more deeply than the sense-making described by Brownell ( 1945 ).

There are plenty of making-sense opportunities in classroom instruction. For example, kindergarten children are often given opportunities to play with manipulatives like cube trains and snub cubes, to explore and learn about patterns, numbers, and measurement through various connections. The recording of such activities typically results in numerical expressions or operations of these connections. In addition, such activities can also serve as a context to encourage students to design and create a way of “recording” these connections directly with a drawing line next to the connected train cubes. Such a design activity will help students to develop the concept of a number line that includes the original/starting point, unit, and direction (i.e., making mathematics make sense), instead of introducing the number line to students as a mathematical concept being “given” years later.

Learning how to provide students with opportunities to develop mathematics may occur with experience. Huang et al. ( 2010 ) found that expert and novice teachers in China both valued students’ mastering of mathematical knowledge and skills and their development in mathematical thinking methods and abilities. However, novice teachers were particularly concerned about the effectiveness of their guidance, in contrast to expert teachers who emphasized the development of students’ mathematical thinking and higher-order thinking abilities and properly dealing with important and difficult content points. The results suggest that teachers’ perceptions and pedagogical practices can change and improve over time. However, it may be worth asking if support for teacher development would accelerate the process.

Connecting changes in mathematics and STEM education

Although it is commonly acknowledged that mathematics is foundational to STEM, mathematics is being related to STEM education at a distance in practice and also in scholarship development (English 2016 , see additional notes at the end of this editorial). Holding the conception of mathematics as products does not support integrating mathematics with other STEM disciplines, as mathematics can be perceived simply as a set of tools for these disciplines. At the same time, mathematics and science have often proceeded along parallel tracks, with mathematics focused on “problem solving” while science has focused on “inquiry.” To better connect mathematics and other disciplines in STEM, we should focus on ideas and thinking development in mathematics (Li et al. 2019a ), unifying instruction from the student perspective (the Teaching for Robust Understanding framework, discussed below).

Emphasizing both sense making and making sense in mathematics education opens opportunities for connections with similar practices in other STEM disciplines. For example, sense making is very much emphasized in science education (Hogan 2019 ; Kapon 2017 ; Odden and Russ 2019 ), often combined with reflections in engineering (Kilgore et al. 2013 ; Turns et al. 2014 ), and also in the context of using technology (e.g., Antonietti and Cantoia 2000 ; Dick and Hollebrands 2011 ). Science is fundamentally about discovery and understanding of the natural world. This notion provides a natural link to mathematical modeling (e.g., Burkhardt 1981 ). Beyond that, in science education, sense making places a heavy focus on the construction and evaluation of explanation (Kapon 2017 ), and can even be defined as a process of constructing an explanation to resolve a perceived gap or conflict in knowledge (Odden and Russ 2019 ). Design and making play vital roles in engineering and technology education (Dym et al., 2005 ), as is student reflection on these experiences (e.g., Turns et al. 2014 ). Indeed, STEM disciplines share the same conceptual process of sense making as learners, individually or in a group, actively engage with the natural or man-made world, explore it, and then develop, test, refine, and use ideas together with specific explanation. If mathematics was conceived as an “empirical” discipline, connections with other STEM disciplines would be strengthened. In philosophical terms, Lakatos ( 1976 ) made similar claims Footnote 1 .

Similar to the emphasis on sense making placed in the Mathematics Curriculum Standards (e.g., NCTM, 1989 , 2000 ), Next Generation Science Standards (NGSS Lead States 2013 ) prompted a shift in science education away from simply knowing science content and procedures to practicing and using science, together with engineering, to make sense of the world and create the future. In a review, Fitzgerald and Palincsar ( 2019 ) concluded sense making is a productive lens for investigating and characterizing great teaching across multiple disciplines.

Mathematics has stronger linkages to creation and design than traditionally imagined. Therefore, its connections to engineering and technology could be much stronger. However, the deep-rooted conception of mathematics as products has traditionally discouraged students and teachers from considering and valuing design and design thinking (Li et al. 2019b ). Conceiving mathematics as making sense should help promote conceptual changes in mathematical practice to value idea generation and design activity. Connections generated from such a shift will support teaching and learning not only in individual STEM disciplines, but also in integrated STEM education.

At the same time, although STEM education as a commonly recognized field does not have a long history (Li 2014 , 2018a ), its rapid development can help introduce ideas for exploring how mathematics can be taught and learned. For example, the concept of projects is common in engineering professional practice, and the project-based learning (PjBL) as an instructional approach is a key component in some engineering programs (e.g., Berger 2016 ; de los Ríos et al. 2010 ; Mills and Treagust 2003 ). de los Ríos et al. ( 2010 ) highlighted three main advantages of PjBL: (1) development in technical, personal, and contextual competences; (2) students’ engagement with real problems from professional contexts; and (3) collaborative learning facilitated through the integration of teaching and research. Such advantages are important for students’ learning of mathematics and are aligned well with efforts to develop 21 st century skills, including problem solving, communication, collaboration, and critical thinking.

Design-based learning (DBL) is another instructional approach commonly used in engineering and technology fields. Gómez Puente et al. ( 2013 ) conducted a sampled review and concluded that DBL projects consist of open-ended, hands-on, authentic, and multidisciplinary design tasks. Teachers using DBL facilitate both the process for students to gain domain-specific knowledge and thinking activities to generate innovative solutions. Such features could be adapted for mathematics education, especially integrated STEM education, in concert with design and design thinking. In addition to a few examples discussed above about making sense in mathematics, there is a growing body of publications developed by and for mathematics teachers with specific examples of investigations, design projects, and instructional activities associated with STEM (Li et al. 2019b ).

A framework for helping students to gain important experiences in and through mathematics, as connected to other disciplines in STEM

For observing and evaluating classroom instruction in general and mathematics classroom instruction in specific, there are several widely used frameworks and rubrics available. However, a trial use of selected frameworks with sampled mathematics classroom instruction episodes suggested their disagreements on what counts as high-quality instruction, especially with aspects on disciplinary thinking being valued and relevant classroom practices (Schoenfeld et al. 2018 ). The results suggest the importance of choice making, when we consider a framework in discussing and evaluating teaching practices.

Our discussion above highlights the importance of shifting away from viewing mathematics simply as a set of static knowledge and skills, to focusing on ideas and thinking development in teaching and learning mathematics. Further discussion of several aspects of changes specifies the needs of developing and using practices associated with sense making, making sense, and connecting mathematics and STEM education for changes.

To support effective mathematics instruction, we propose the use of the Teaching for Robust Understanding (TRU) framework to help characterize powerful learning environments. With the conception of mathematics as “empirical” and a focus on students’ experience, then the focus of instruction should also be changed. We argue that shift is from instruction conceived as “what should the teacher do” to instruction conceived as “what mathematical experiences should students have in order for them to develop into powerful thinkers?” It is the shift in the frame of TRU that makes it so powerful and pertinent for all these proposed changes. Moreover, TRU only uses a small number of actionable dimensions after distilling the literature on teaching for robust or powerful understanding. That makes TRU a practical mechanism for problematizing instruction.

Figure 1 presents the TRU Math framework that identifies five key dimensions along which powerful classroom environments can be characterized: the mathematics; cognitive demand; equitable access; agency, ownership, and identity; and formative assessment. These five dimensions were distilled from an extensive literature review, thus capturing what the literature considers to be essential. They were tested against classroom videotapes and data on student performance, and the results indicated that classrooms that did well on the TRU dimensions produced students who did correspondingly well on tests of mathematical knowledge, thinking, and problem solving (e.g., Schoenfeld 2014 , 2019 ). In brief, the argument regarding the importance of the five dimensions of TRU Math is as follows. First, the quality of the mathematics discussed (dimension 1) is critical. What individual students learn is unlikely to be richer than what they experience in the classroom. Whether individual students’ understanding rises to the level of what is discussed/presented in the classroom depends on other factors, which are captured in the remaining four dimensions. For example, you surely have had the experience, at a lecture, of hearing beautiful content presented, and then not being able to do any of the assigned problems! The remaining four dimensions capture aspects needed to support the development of all students with respect to sense making, making sense, ownership, and feedback loop. Dimension 2: Cognitive Demand. Are students engaged in sense making and making sense? Are they engaged in “productive struggle”? Dimension 3: Equitable Access. Are all students fully engaged with the central content and practices of the domain so that every student can profit from it? Dimension 4: Agency, Ownership, and Identity. Do all students have opportunities to develop idea ownership and mathematical agency? Dimension 5: Formative Assessment. Are students encouraged and supported to share their thinking with a meaningful feedback loop for instructional adjustment and improvement?

The TRU Mathematics Framework: The five dimensions of powerful mathematics classrooms

The first key point about TRU is that students learn more in classrooms that are powerful along the five TRU dimensions. Second, the shift of attention from the teacher to the environment is fundamentally important. The key question is not “Is the teacher doing particular things to support learning?”; instead, it is, “Are students experiencing instruction so that it is conducive to their growth as mathematical thinkers and learners?” Third, the framework is not prescriptive; it respects teacher autonomy. There are many ways to be an excellent teacher. The question is, Does the learning environment created by the teacher provide each student rich opportunities along the five dimensions of the framework? Specifically, in describing the dimensions of powerful instruction, the framework serves to problematize instruction. Asking “how am I doing along each dimension; how can I improve?” can lead to richer instruction without prescribing or imposing a particular style or particular norms on teachers.

Extending to STEM education

Now, we suggest the following. If you teach biology, chemistry, physics, engineering, or any other STEM field, replace “mathematics” in Fig. 1 with your discipline. The first dimension is about rich content and practices in your field. And the remaining four dimensions are about necessary aspects of your students’ classroom engagement with the discipline. Practices associated with sense making, making sense, and STEM education are all be reflected in these five dimensions, with central attention on students’ experience in such classroom environments. Although the TRU framework was originally developed for characterizing effective mathematics classroom environments, it has been carefully framed in a way that is applicable to many different disciplines (Schoenfeld 2014 ). Our discussion above already specified why sense making, making sense, and specific instructional approaches like PjBL and DBL are shared across disciplines in STEM education. Thus, the TRU framework is applicable to other STEM disciplines. The natural analogue of the TRU framework for any field is given in Fig. 2 .

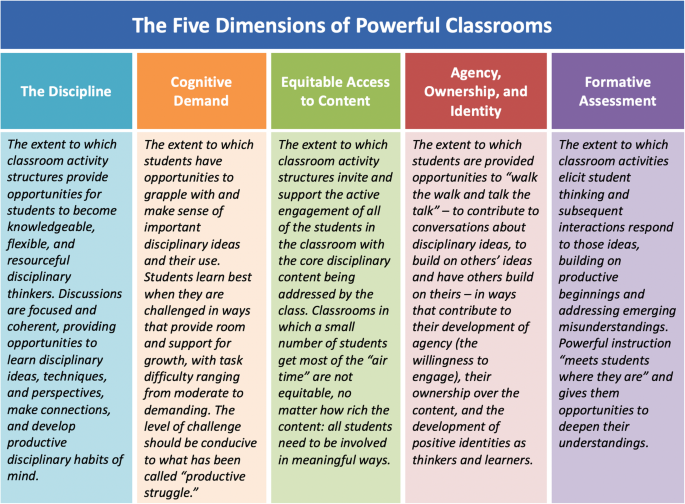
The domain-general version of the TRU framework

Both the San Francisco Unified School District and the Chicago Public Schools adopted the TRU Math framework and found results within mathematics sufficiently promising that they expanded their efforts to all subject areas for professional development and instruction, using the domain-general TRU framework. Work is still in its early stages. Current efforts might be best conceptualized as a laboratory for exploration rather than a promissory note for improvement across all different disciplines. It will take time to accumulate data to show effectiveness. For further information about the domain-general TRU framework and tools for professional development are available at the TRU framework website, https://truframework.org/

Finally, as a framework, TRU is not a set of specific tools or guidelines, although it can be used to guide their development. To help lead our discussion to something more practical, we can use the framework to check and identify aspects that are typically under-emphasized and move them to center stage in order to improve classroom instruction. Specifically, the following is a list of sample under-emphasized norms and practices that can be identified (Schoenfeld in press ).

Establishing a climate of inquiry, in which mathematics is experienced as a discipline of exploration and sense making.

Developing students’ ownership of ideas through the process of developing, sharing, refining, and using ideas; concepts and language can come later.

Focusing on big ideas, and not losing the forest for the trees.

Making student thinking central to classroom discourse.

Ensuring that classroom discourse is respectful and inviting.

Where to start? Begin by problematizing teaching and the nature of learning environments

Here we start by stipulating that STEM disciplines as practiced, are living, breathing fields of inquiry. Knowledge is important; ideas are important; practices are important. The list given above applied to all STEM disciplines, not just mathematics.

The issue, then, is developing teacher capacity to craft environments that have the properties described immediately above. Here we share some thoughts, and the topic itself can well be discussed extensively in another paper. To make changes in teaching, it should start with assessing and changing teaching practice itself (Hiebert and Morris 2012 ). Opening up teachers’ perceptions of teaching practices should not be done by telling teachers what to do!—the same rules of learning apply to teachers as they apply to students. Learning environments for teachers should offer teachers the same opportunities for rich engagement, challenge, equitable access, and ownership as we hope students will experience (Schoenfeld 2015 ). Working together with teachers to study and reflect on their teaching practices in light of the TRU framework, we can help teachers to find out what their students are experiencing and why changes are needed. The framework can also help guide teachers to learn what changes would be needed, and to try out changes to learn how their students’ learning may differ. It is this iterative and concrete process that can hopefully help shift participating teachers’ perceptions of mathematics. Many tools for problematizing teaching are available at the TRU web site (see https://truframework.org/ ). If teachers can work together with a focus on selected lessons like what teachers often do in China, the process would help form a school-based learning community that can contribute to not only participating teachers’ practice change but also their expertise improvement (Huang et al. 2011 ; Li and Huang 2013 ).

As reported before (Li 2018b ), publications in the International Journal of STEM Education show a mix of individual-disciplinary and multidisciplinary education in STEM over the past several years. Although one journal’s publications are limited in its scope of providing a picture about the scholarship development related to mathematics and STEM education, it can allow us to get a sense of related development.

If taking a closer look at the journal’s publications over the past three years from 2016 to 2018, we found that the number of articles published with a clear focus on mathematics is relatively small: three (out of 21) in 2016, six (out of 34) in 2017, and five (out of 56) in 2018. At the same time, we should point out that these publications from 2016 to 2018 seem to reflect a trend, over these three years, of moving toward issues that can go beyond mathematics itself, as what was noted before (Li 2018b ). Specifically, for these three articles published in 2016, they are all about mathematics education at either elementary school (Ding 2016 ; Zhao et al. 2016 ) or university levels (Schoenfeld et al. 2016 ). Out of the six published in 2017, three are on mathematics education (Hagman et al. 2017 ; Keller et al. 2017 ; Ulrich and Wilkins 2017 ) and the other three on either teacher professional development (Borko et al. 2017 ; Jacobs et al. 2017 ) or connection with engineering (Jehopio and Wesonga 2017 ). For the five published in 2018, two are on mathematics education (Beumann and Wegner 2018 ; Wilkins and Norton 2018 ) and the other three have close association with other disciplines in STEM (Blotnicky et al. 2018 ; Hayward and Laursen 2018 ; Nye et al. 2018 ). This trend likely reflects a growing interest, with close connection to mathematics, in both mathematics education community and a broader STEM education community of developing and sharing multidisciplinary and interdisciplinary scholarship.

Availability of data and materials

Not applicable

Interestingly, Lakatos was advised by both Popper and Pólya—his ideas being in some ways a unification of Pólya’s emphasis on mathematics as an empirical discipline and Popper’s reflections on the nature of the scientific endeavor.

Antonietti, A., & Cantoia, M. (2000). To see a painting versus to walk in a painting: An experiment on sense-making through virtual reality. Computers & Education, 34 , 213–223.

Article   Google Scholar  

Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14 (3), 24–35.

Google Scholar  

Ashlock, R. B. (2010). Error patterns in computation (Tenth Edition) . Boston, MA: Allyn & Bacon.

Banilower, E. R., Smith, P. S., Weiss, I. R., Malzahn, K. A., Campbell, K. M., et al. (2013). Report of the 2012 national survey of science and mathematics education. Horizon Research, Chapel Hill, NC. Retrieved from http://www.nnstoy.org/download/stem/2012%20NSSME%20Full%20Report.pdf

Berger, C. (2016). Engineering is perfect for K-5 project-based learning. Engineering is Elementary (EiE) Blog, https://blog.eie.org/engineering-is-perfect-for-k-5-project-based-learning

Beumann, S. & Wegner, S.-A. (2018). An outlook on self-assessment of homework assignments in higher mathematics education. International Journal of STEM Education, 5 :55. https://doi.org/10.1186/s40594-018-0146-z

Blotnicky, K. A., Franz-Odendaal, T., French, F., & Joy, P. (2018). A study of the correlation between STEM career knowledge, mathematics self-efficacy, career interests, and career activities on the likelihood of pursuing a STEM career among middle school students. International Journal of STEM Education, 5 :22. https://doi.org/10.1186/s40594-018-0118-3

Borko, H., Carlson, J., Mangram, C., Anderson, R., Fong, A., Million, S., Mozenter, S., & Villa, A. M. (2017). The role of video-based discussion in model for preparing professional development leaders. International Journal of STEM Education, 4 :29. https://doi.org/10.1186/s40594-017-0090-3

Boyer, C. B. (1991). A history of mathematics (2nd ed.) . New York: Wiley.

Brownell, W. A. (1945). When is arithmetic meaningful? The Journal of Educational Research, 38 (7), 481–498.

Burkhardt, H. (1981). The real world and mathematics . Glasgow: Blackie, reissued Nottingham: Shell Centre Publications.

Carpenter, T., Fennema, E., & Franke, M. (1997). Cognitively guided instruction: A knowledge base for reform in primary mathematics instruction. Elementary School Journal, 97 , 3–20.

Carpenter, T., Franke, M., Jacobs, V. R., & Fennema, E. (1998). A longitudinal study of invention and understanding in children’s multidigit addition and subtraction. Journal for Research in Mathematics Education, 29 (1), 3–20.

Committee on STEM Education, National Science & Technology Council, the White House (2018). Charting a course for success: America’s strategy for STEM education . Washington, DC. https://www.whitehouse.gov/wp-content/uploads/2018/12/STEM-Education-Strategic-Plan-2018.pdf Retrieved on 18 January, 2019.

Common Core State Standards Initiative (CCSSI). (2010). Common core state standards for mathematics . Retrieved from http://www.corestandards.org/Math/Practice

Cooney, T (1987). The issue of reform: What have we learned from yesteryear? In Mathematical Sciences Education Board, The teacher of mathematics: Issues for today and tomorrow (pp. 17-35). Washington, DC: National Academy Press.

Coppin, C. A., Mahavier, W. T., May, E. L., & Parker, E. (2009). The Moore Method . Washington, DC: Mathematical Association of America.

Davis, P., & Hersh, R. (1980). The mathematical experience . Boston: Birkhauser.

de los Ríos, I., Cazorla, A., Díaz-Puente, J. M., & Yagüe, J. L. (2010). Project–based learning in engineering higher education: Two decades of teaching competences in real environments. Procedia Social and Behavioral Sciences, 2 , 1368–1378.

Devlin, K. (2000). The four faces of mathematics. In M. J. Burke & F. R. Curcio (Eds.), Learning Mathematics for a New Century: 2000 Yearbook of the National Council of Teachers of Mathematics (pp. 16–27). Reston, VA: NCTM.

Devlin, K. (2012). Introduction to mathematical thinking. Stanford, CA: The author.

Dick, T. P., & Hollebrands, K. F. (2011). Focus on high school mathematics: Technology to support reasoning and sense making . Reston, VA: NCTM.

Ding, M. (2016). Developing preservice elementary teachers’ specialized content knowledge: The case of associative property. International Journal of STEM Education, 3 , 9 https://doi.org/10.1186/s40594-016-0041-4 .

Dossey, J. A. (1992). The nature of mathematics: Its role and its influence. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 39–48). New York: MacMillan.

Dossey, J. A., McCrone, S. S., & Halvorsen, K. T. (2016). Mathematics education in the United States 2016: A capsule summary fact book . Reston, VA: The National Council of Teachers of Mathematics.

Dym, C. L., Agogino, A. M., Eris, O., Frey, D. D., & Leifer, L. J. (2005). Engineering design thinking, teaching, and learning. Journal of Engineering Education, 94 (1), 103–120.

English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3:3, https://doi.org/10.1186/s40594-016-0036-1

Fisher, C. (1990). The research agenda project as prologue. Journal for Research in Mathematics Education, 21 , 81–89.

Fitzgerald, M. S., & Palincsar, A. S. (2019). Teaching practices that support student sensemaking across grades and disciplines: A conceptual review. Review of Research in Education, 43 , 227–248.

Fritz, A., Haase, V. G., & Rasanen, P. (Eds.). (2019). International handbook of mathematical learning difficulties . Cham, Switzerland: Springer.

Gee, J. P. (2005). What would a state of the art instructional video game look like? Innovate: Journal of Online Education, 1 (6) Retrieved from https://nsuworks.nova.edu/innovate/vol1/iss6/1 .

Gómez Puente, S. M., van Eijck, M., & Jochems, W. (2013). A sampled literature review of design-based learning approaches: A search for key characteristics. International Journal of Technology and Design Education . https://doi.org/10.1007/s10798-012-9212-x .

Hagman, J. E., Johnson, E., & Fosdick, B. K. (2017). Factors contributing to students and instructors experiencing a lack of time in college calculus. International Journal of STEM Education, 4 , 12 https://doi.org/10.1186/s40594-017-0070-7 .

Hayward, C. N. & Laursen, S. L. (2018). Supporting instructional change in mathematics: Using social network analysis to understand online support processes following professional development workshops. International Journal of STEM Education, 5 :28. https://doi.org/10.1186/s40594-018-0120-9

Hersh, R. (1986). Some proposals for reviving the philosophy of mathematics . In T. Tymoczko (Ed.), New directions in the philosophy of mathematics (pp. 9–28). Boston: Birkhauser.

Hiebert, J., & Morris, A. K. (2012). Teaching, rather than teachers, as a path toward improving classroom instruction. Journal of Teacher Education, 63 (2), 92–102.

Hogan, M. (2019). Sense-making is the core of NGSS. In Illuminate education blog, https://www.illuminateed.com/blog/2019/03/sense-making-is-the-core-of-ngss/ Accessed 15 Oct 2019.

Huang, R., Li, Y., & He, X. (2010). What constitutes effective mathematics instruction: A comparison of Chinese expert and novice teachers’ views. Canadian Journal of Science, Mathematics and Technology Education, 10 (4), 293-306. https://doi.org/10.1080/14926156.2010.524965

Huang, R., Li, Y., Zhang, J., & Li, X. (2011). Improving teachers’ expertise in mathematics instruction through exemplary lesson development. ZDM – The International Journal on Mathematics Education, 43 (6-7), 805–817.

Jacobs, J., Seago, N., & Koellner, K. (2017). Preparing facilitators to use and adapt mathematics professional development materials productively. International Journal of STEM Education, 4 , 30 https://doi.org/10.1186/s40594-017-0089-9 .

Jehopio, P. J., & Wesonga, R. (2017). Polytechnic engineering mathematics: assessing its relevance to the productivity of industries in Uganda. International Journal of STEM Education, 4 , 16 https://doi.org/10.1186/s40594-017-0078-z .

Kapon, S. (2017). Unpacking sensemaking. Science Education, 101 (1), 165–198.

Keitel, C. (2006). ‘Setting a task’ in German schools: Different frames for different ambitions. In D. Clarke, C. Keitel, & Y. Shimizu (Eds.), Mathematics classrooms in 12 countries: The insiders’ perspective (pp. 37–58). Rotterdam Netherlands: Sense Publishers.

Keller, R. E., Johnson, E., & DeShong, S. (2017). A structural equation model looking at student’s participatory behavior and their success in Calculus I. International Journal of STEM Education, 4 , 24 https://doi.org/10.1186/s40594-017-0093-0 .

Kilgore, D., Sattler, B., & Turns, J. (2013). From fragmentation to continuity: Engineering students making sense of experience through the development of a professional portfolio. Studies in Higher Education, 38 (6), 807–826.

Kline, M. (1973). Why Johnny can’t add: The failure of new math . New York: St. Martin’s.

Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery . Cambridge, England: Cambridge University Press.

Book   Google Scholar  

Leung, F. K. S., & Li, Y. (Eds.). (2010). Reforms and issues in school mathematics in East Asia – Sharing and understanding mathematics education policies and practices . Rotterdam, Netherlands: Sense Publishers.

Li, Y. (2014). International Journal of STEM Education – A platform to promote STEM education and research worldwide. International Journal of STEM Education, 1 , 1 https://doi.org/10.1186/2196-7822-1-1 .

Li, Y. (2018a). Journal for STEM Education Research – Promoting the development of interdisciplinary research in STEM education. Journal for STEM Education Research, 1 (1-2), 1–6 https://doi.org/10.1007/s41979-018-0009-z .

Li, Y. (2018b). Four years of development as a gathering place for international researcher and readers in STEM education. International Journal of STEM Education, 5 , 54 https://doi.org/10.1186/s40594-018-0153-0 .

Li, Y., & Huang, R. (Eds.). (2013). How Chinese teach mathematics and improve teaching . New York: Routledge.

Li, Y., & Lappan, G. (Eds.). (2014). Mathematics curriculum in school education . Dordrecht: Springer.

Li, Y., Schoenfeld, A. H., diSessa, A. A., Grasser, A. C., Benson, L. C., English, L. D., & Duschl, R. A. (2019a). On thinking and STEM education. Journal for STEM Education Research, 2 (1), 1–13. https://doi.org/10.1007/s41979-019-00014-x .

Li, Y., Schoenfeld, A. H., diSessa, A. A., Grasser, A. C., Benson, L. C., English, L. D., & Duschl, R. A. (2019b). Design and design thinking in STEM education. Journal for STEM Education Research, 2 (2), 93-104. https://doi.org/10.1007/s41979-019-00020-z .

Li, Y., Silver, E. A., & Li, S. (Eds.). (2014). Transforming mathematics instruction: Multiple approaches and practices . Cham, Switzerland: Springer.

Luttenberger, S., Wimmer, S., & Paechter, M. (2018). Spotlight on math anxiety. Psychology Research and Behavior Management, 11 , 311–322.

McCallum, W. (2018). Sense-making and making sense. https://blogs.ams.org/matheducation/2018/12/05/sense-making-and-making-sense/ Retrieved on October 1, 2019.

Mills, J. E. & Treagust, D. F. (2003). Engineering education – Is problem-based or project-based learning the answer? Australasian Journal of Engineering Education , https://www.researchgate.net/profile/Nathan_Scott2/publication/238670687_AUSTRALASIAN_JOURNAL_OF_ENGINEERING_EDUCATION_Co-Editors/links/0deec53a08c7553c37000000.pdf Retrieved on October 15, 2019.

National Council of Teachers of Mathematics (NCTM). (1989). Curriculum and evaluation standards for school mathematics . Reston, VA: NCTM.

National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics . Reston, VA: NCTM.

NGSS Lead States. (2013). Next generation science standards: For states, by states . Washington, DC: National Academies Press.

Nye, B., Pavlik Jr., P. I., Windsor, A., Olney, A. M., Hajeer, M., & Hu, X. (2018). SKOPE-IT (Shareable Knowledge Objects as Portable Intelligent Tutors): Overlaying natural language tutoring on an adaptive learning system for mathematics. International Journal of STEM Education, 5 , 12 https://doi.org/10.1186/s40594-018-0109-4 .

Odden, T. O. B., & Russ, R. S. (2019). Defining sensemaking: Bringing clarity to a fragmented theoretical construct. Science Education, 103 , 187–205.

Parrish, S. D. (2011). Number talks build numberical reasoning. Teaching Children Mathematics, 18 (3), 198–206.

Rattan, A., Good, C., & Dweck, C. S. (2012). “It’s ok – Not everyone can be good at math”: Instructors with an entity theory comfort (and demotivate) students. Journal of Experimental Social Psychology . https://doi.org/10.1016/j.jesp.2011.12.012 .

Schoenfeld, A. H. (1988). When good teaching leads to bad results: The disasters of “well-taught” mathematics courses. Educational Psychologist, 23 (2), 145–166.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334–370). New York: MacMillan.

Schoenfeld, A. H. (2001). Mathematics education in the 20th century. In L. Corno (Ed.), Education across a century: The centennial volume (100th Yearbook of the National Society for the Study of Education) (pp. 239–278). Chicago, IL: National Society for the Study of Education.

Schoenfeld, A. H. (2014). What makes for powerful classrooms, and how can we support teachers in creating them? A story of research and practice, productively interwined. Educational Researcher, 43 (8), 404–412. https://doi.org/10.3102/0013189X1455 .

Schoenfeld, A. H. (2015). Thoughts on scale. ZDM, the International Journal of Mathematics Education, 47 , 161–169. https://doi.org/10.1007/s11858-014-0662-3 .

Schoenfeld, A. H. (2019). Reframing teacher knowledge: A research and development agenda. ZDM – The International Journal on Mathematics Education . https://doi.org/10.1007/s11858-019-01057-5

Schoenfeld, A. H. (in press). Mathematical practices, in theory and practice. ZDM – The International Journal on Mathematics Education .

Schoenfeld, A. H., Floden, R., El Chidiac, F., Gillingham, D., Fink, H., Hu, S., Sayavedra, A., Weltman, A., & Zarkh, A. (2018). On classroom observations. Journal for STEM Educ Res, 1 (1-2), 34–59 https://doi.org/10.1007/s41979-018-0001-7 .

Schoenfeld, A. H., Thomas, M., & Barton, B. (2016). On understanding and improving the teaching of university mathematics. International Journal of STEM Education, 3 , 4 https://doi.org/10.1186/s40594-016-0038-z .

Smith, J., diSessa, A., & Roschelle, J. (1993). Misconceptions reconceived: A constructivist analysis of knowledge in transition. Journal of the Learning Sciences, 3 (2), 115–163.

Sowder, J. (1992). Estimation and number sense. In D. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 371–389). New York: MacMillan.

Stanic, G. M. A., & Kilpatrick, J. (1992). Mathematics curriculum reform in the United States: A historical perspective. International Journal of Educational Research, 17 (5), 407–417.

Sun, K. L. (2018). The role of mathematics teaching in fostering student growth mindset. Journal for Research in Mathematics Education, 49 (3), 330–355.

Turns, J. A., Sattler, B., Yasuhara, K., Borgford-Parnell, J. L., & Atman, C. J. (2014). Integrating reflection into engineering education. Proceedings of 2014 American Society of Engineering Education Annual Conference , Paper ID #9230.

Tymoczko, T. (1986). New directions in the philosophy of mathematics . Boston: Birkhauser.

Ulrich, C., & Wilkins, J. L. M. (2017). Using written work to investigate stages in sixth-grade students’ construction and coordination of units. International Journal of STEM Education, 4 , 23 https://doi.org/10.1186/s40594-017-0085-0 .

Wilkins, J. L. M., & Norton, A. (2018). Learning progression toward a measurement concept of fractions. International Journal of STEM Education, 5 , 27 https://doi.org/10.1186/s40594-018-0119-2 .

Zhao, X., Van den Heuvel-Panhuizen, M., & Veldhuis, M. (2016). Teachers’ use of classroom assessment techniques in primary mathematics education – An explorative study with six Chinese teachers. International Journal of STEM Education, 3 , 19 https://doi.org/10.1186/s40594-016-0051-2 .

Download references

Acknowledgments

Many thanks to Jeffrey E. Froyd for his careful review and detailed comments on an earlier version of this editorial that help improve its readability and clarity. Thanks also go to Marius Jung for his valuable feedback.

Author information

Authors and affiliations.

Texas A&M University, College Station, TX, 77843-4232, USA

University of California at Berkeley, Berkeley, CA, USA

Alan H. Schoenfeld

You can also search for this author in PubMed   Google Scholar

Contributions

Both authors contributed ideas to conceptualize this article. YL took the lead in developing and drafting the article, and AHS reviewed drafts and contributed to revisions. Both authors read and approved the final manuscript.

Corresponding author

Correspondence to Yeping Li .

Ethics declarations

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Cite this article.

Li, Y., Schoenfeld, A.H. Problematizing teaching and learning mathematics as “given” in STEM education. IJ STEM Ed 6 , 44 (2019). https://doi.org/10.1186/s40594-019-0197-9

Download citation

Received : 15 November 2019

Accepted : 19 November 2019

Published : 19 December 2019

DOI : https://doi.org/10.1186/s40594-019-0197-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Design-based learning
• Making sense
• Mathematics
• Project-based learning
• Sense making
• STEM education

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Problem-Based Instruction in Middle and High School Math

PBI allows students to investigate real-world mathematical questions, increasing engagement with and understanding of course material.

Coach , facilitator , and guide on the side are phrases we have heard being used to describe the teacher’s role in PBI (problem-based instruction). Our idea of PBI is that students are exploring, inquiring, and crafting their own knowledge instead of being spoon-fed information by their teacher. In PBI the teacher moves from being the main disseminator of knowledge to a tool students use to help them guide their own exploration. The teacher must be well prepared and well versed in the content to be able to guide students to appropriate resources, answer questions, and ensure students remain on the correct trajectory with their inquiry. It is the role of the teacher as the content expert to come alongside the students to share resources, encourage, ask probing questions, and ensure students have a supportive environment in which to explore, inquire, and craft their understanding.

The preparations for a teacher in a PBI setting come largely before a PBI lesson is launched in the classroom. Teachers need to prepare resources, craft the driving question or problem scenario, and ensure all project aspects are planned and clear. If connections are being made to community entities or entities outside of the classroom, those arrangements must be secured by the teacher before initiating the PBI so that student experiences are well crafted and flow smoothly. While planning the PBI experience, teachers must also be intimately aware of their students’ learning needs.

Students learn at different rates and will seek different levels of content exploration. Scaffolding a lesson to accommodate student learning needs is a necessity in PBI. Teachers must know how to meet individual learning needs and what accommodations will have to be made, and then seek ways to provide support and structure within this framework. Teachers should also be familiar with the instructional learning goals targeted by the PBI lesson to ensure accuracy and adherence to these learning goals throughout the lesson.

Perhaps the most crucial trait of a teacher in a PBI lesson is flexibility. While teachers can plan, plan, and plan, it is almost guaranteed that something will not go as planned. Sometimes students stretch beyond the planned learning target and go deeper with their inquiry than expected. Other times students will hit a roadblock and will require extra support and encouragement. Sometimes schedules change, unexpected events occur, and the pacing for the lesson becomes offset. Teacher flexibility and fluidity will help encourage students to remain focused on their inquiry while knowing their knowledge journey is supported by their teacher.

PBI FROM THE STUDENT’S PERSPECTIVE

“When am I ever going to use this?” “Can you just tell me the steps needed to do this?” If you are or ever have been a math teacher, these are questions you have probably heard from students repeatedly and probably have become frustrated by. However, instead of getting frustrated, we should ask ourselves why these questions continue to permeate our mathematics classrooms. The answer? Students are not engaged in authentic mathematics while they are learning, but rather they are following prescribed steps in a rote memorized fashion to reach an answer. True learning is not regurgitating steps but rather seeing the connectedness of content and understanding the practical usability of different solution strategies.

In traditional mathematics classrooms, the teacher stands at the front of the room, demonstrates several step-by-step examples (typically devoid of real-world context) of a new skill, and then releases students to try it independently. As soon as students begin to struggle, the teacher walks them through the problem step-by-step. Students are exposed to word problems and applications at the end of the unit and then only minimally. As a result, students have developed a mathematical identity that defines their role in math class not as learners of mathematics and problem solvers but as performers whose only goal is to get questions right (Boaler, 2022). They disconnect from mathematics because they view it as rote procedures with no interesting or practical application.

PBI also allows students to learn and practice critical 21st-century skills needed to be successful no matter where their path in life and career takes them. Because PBI is collaborative in nature, students are learning to work together in team settings. They are learning to discuss their thoughts and share ideas so that others can understand and engage in dialogue around the shared comments and disseminate their findings/comments/ideas through various verbal, written, or multimedia platforms.

No matter how clearly or repeatedly a teacher explains a mathematical concept or skill, understanding can occur only when students connect new information with previously learned skills. Sure, using traditional methods may support students in memorizing enough steps to allow them to pass their unit assessment or even their end-of-course assessment, but is that truly learning? Rote regurgitation of memorized steps rarely results in long-term learning that translates to solving real-life problems or even to subsequent courses taken during their academic careers. To achieve this level of mathematical understanding, students must be able to engage in authentic mathematical tasks that allow them to collaborate, problem-solve, and problematize. In other words, mathematics is not something students learn by watching; it’s something they learn by doing. One of our students described PBI as a puzzle: “You look for pieces you need when you need them, and then all of a sudden, the whole picture comes together.”

In contrast to student experiences in traditional classrooms, students in a PBI environment feel immersed in their learning. They begin to believe that their voice matters and immediately see the applicability and practicality of what they are learning. Instead of “When am I ever going to use this?” and “Just tell me what the steps are,” students ask questions that prompt exploration, resulting in learning in context. Yes, students are working with manipulatives; yes, sometimes they complete practice worksheets; yes, students are working with their teacher(s) and peer(s), but each activity is carefully crafted toward its purpose relative to the problem/task to be solved/completed. In PBI lessons, there is no longer a feeling that students are learning content because it is in chapter 2 and they just finished chapter 1, so chapter 2 is what comes next . . . instead, the content is explored in context to give meaning and applicability.

Transitioning from a traditional classroom environment to one grounded in PBI can be challenging for students. PBI pushes students to think. PBI pushes students to go beyond what they think they know and to use what they know to “figure out” new concepts. PBI is different from how most students have been learning mathematics for years—it pushes them outside their comfort zone. As a result, students will push back. They will complain.

However, we can tell you from firsthand experience that if teachers remain consistent and support students through this struggle without compromising the foundations that PBI is built upon, students will not only accept this new way of learning mathematics but will thrive because of it. One of our students explained it this way: “This class is different. We don’t just cover content through lectures and you [the teacher] telling us what to do. We explore and discuss ideas, and suddenly I feel like I just know it. I feel like I have learned more in this math class than all of my other math classes combined.”

Reprinted by permission of the Publisher. From Sarah Ferguson and Denise L. Polojac-Chenoweth, Implementing Problem-Based Instruction in Secondary Mathematics Classrooms , New York: Teachers College Press. Copyright © 2024 by Teachers College, Columbia University. All rights reserved.

• Business & Money
• Management & Leadership

Enjoy fast, free delivery, exclusive deals, and award-winning movies & TV shows with Prime Try Prime and start saving today with fast, free delivery

Amazon Prime includes:

Fast, FREE Delivery is available to Prime members. To join, select "Try Amazon Prime and start saving today with Fast, FREE Delivery" below the Add to Cart button.

• Cardmembers earn 5% Back at Amazon.com with a Prime Credit Card.
• Unlimited Free Two-Day Delivery
• Streaming of thousands of movies and TV shows with limited ads on Prime Video.
• A Kindle book to borrow for free each month - with no due dates
• Listen to over 2 million songs and hundreds of playlists
• Unlimited photo storage with anywhere access

Important:  Your credit card will NOT be charged when you start your free trial or if you cancel during the trial period. If you're happy with Amazon Prime, do nothing. At the end of the free trial, your membership will automatically upgrade to a monthly membership.

Buy new: $97.75

Return this item for free.

Free returns are available for the shipping address you chose. You can return the item for any reason in new and unused condition: no shipping charges

• Go to your orders and start the return
• Select the return method

Download the free Kindle app and start reading Kindle books instantly on your smartphone, tablet, or computer - no Kindle device required .

Read instantly on your browser with Kindle for Web.

Using your mobile phone camera - scan the code below and download the Kindle app.

Image Unavailable

• To view this video download Flash Player

Teaching and Learning Mathematical Problem Solving 1st Edition

Purchase options and add-ons.

A provocative collection of papers containing comprehensive reviews of previous research, teaching techniques, and pointers for direction of future study. Provides both a comprehensive assessment of the latest research on mathematical problem solving, with special emphasis on its teaching, and an attempt to increase communication across the active disciplines in this area.

• ISBN-10 0898597595
• ISBN-13 978-0898597592
• Edition 1st
• Publication date June 12, 1985
• Language English
• Dimensions 7.01 x 1.09 x 10 inches
• Print length 484 pages
• See all details

Editorial Reviews

"...a valuable resource for anyone interested in human mathematical performance." ― Contemporary Psychology

"...it is always a pleasure to find and read a well-planned, well-written, and well-organized book on the subject...it would be very helpful to anyone pursuing research in mathematical problem solving." ― Mathematics Teacher

About the Author

Product details.

• Publisher ‏ : ‎ Routledge; 1st edition (June 12, 1985)
• Language ‏ : ‎ English
• Paperback ‏ : ‎ 484 pages
• ISBN-10 ‏ : ‎ 0898597595
• ISBN-13 ‏ : ‎ 978-0898597592
• Lexile measure ‏ : ‎ 1360L
• Item Weight ‏ : ‎ 1.98 pounds
• Dimensions ‏ : ‎ 7.01 x 1.09 x 10 inches

Customer reviews

Customer Reviews, including Product Star Ratings help customers to learn more about the product and decide whether it is the right product for them.

To calculate the overall star rating and percentage breakdown by star, we don’t use a simple average. Instead, our system considers things like how recent a review is and if the reviewer bought the item on Amazon. It also analyzed reviews to verify trustworthiness.

No customer reviews

• Amazon Newsletter
• About Amazon
• Accessibility
• Sustainability
• Press Center
• Investor Relations
• Amazon Devices
• Amazon Science
• Start Selling with Amazon
• Sell apps on Amazon
• Supply to Amazon
• Protect & Build Your Brand
• Become an Affiliate
• Become a Delivery Driver
• Start a Package Delivery Business
• Advertise Your Products
• Self-Publish with Us
• Host an Amazon Hub
• › See More Ways to Make Money
• Amazon Visa
• Amazon Store Card
• Amazon Secured Card
• Amazon Business Card
• Shop with Points
• Credit Card Marketplace
• Reload Your Balance
• Amazon Currency Converter
• Your Account
• Your Orders
• Shipping Rates & Policies
• Amazon Prime
• Returns & Replacements
• Manage Your Content and Devices
• Recalls and Product Safety Alerts
• Conditions of Use
• Privacy Notice
• Your Ads Privacy Choices

Center for Teaching

Teaching problem solving.

Print Version

Tips and Techniques

Expert vs. novice problem solvers, communicate.

• Have students  identify specific problems, difficulties, or confusions . Don’t waste time working through problems that students already understand.
• If students are unable to articulate their concerns, determine where they are having trouble by  asking them to identify the specific concepts or principles associated with the problem.
• In a one-on-one tutoring session, ask the student to  work his/her problem out loud . This slows down the thinking process, making it more accurate and allowing you to access understanding.
• When working with larger groups you can ask students to provide a written “two-column solution.” Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column. This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems. Two-Column Solution (Math) Two-Column Solution (Physics)

Encourage Independence

• Model the problem solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts and make your thinking clear
• Have students work through problems on their own. Ask directing questions or give helpful suggestions, but  provide only minimal assistance and only when needed to overcome obstacles.
• Don’t fear  group work ! Students can frequently help each other, and talking about a problem helps them think more critically about the steps needed to solve the problem. Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others

Be sensitive

• Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning. It is important to recognize this when students come to us for help, and to give each student some feeling of mastery. Do this by providing  positive reinforcement to let students know when they have mastered a new concept or skill.

Encourage Thoroughness and Patience

• Try to communicate that  the process is more important than the answer so that the student learns that it is OK to not have an instant solution. This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem solving through a step-by step process.

Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem solving skills,  a teacher should be aware of principles and strategies of good problem solving in his or her discipline .

The mathematician George Polya captured the problem solving principles and strategies he used in his discipline in the book  How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes  a summary of Polya’s problem solving heuristic as well as advice on the teaching of problem solving.

Teaching Guides

• Online Course Development Resources
• Principles & Frameworks
• Pedagogies & Strategies
• Reflecting & Assessing
• Challenges & Opportunities
• Populations & Contexts

Quick Links

• Services for Departments and Schools
• Examples of Online Instructional Modules

Mathematical knowledge for teaching teachers: knowledge used and developed by mathematics teacher educators in learning to teach via problem solving

• Published: 27 October 2017
• Volume 21 , pages 429–450, ( 2018 )

Cite this article

• Joanna O. Masingila 1 ,
• Dana Olanoff 2 &
• Patrick M. Kimani 3  

3213 Accesses

24 Citations

4 Altmetric

Explore all metrics

In this study, we report on what types of mathematical knowledge for teaching teachers (MKTT) mathematics teacher educators (MTEs) use and develop when they work together and reflect on their teaching in a Community of Practice while helping prospective primary teachers (PTs) generate their own mathematical knowledge for teaching in learning mathematics via problem solving. Two novice MTEs worked with an experienced MTE and reflected on the process of learning to teach via problem solving and supporting PTs in developing deep understandings of foundational mathematical ideas. Taking a position of inquiry as stance, we examined our experiences teaching mathematics content courses for PTs via problem solving. We found that all of the MTEs used and developed some MKTT through (a) understanding and deciding on the mathematical goals of both the individual lessons and the two-course sequence as a whole, (b) choosing and facilitating tasks, and (c) using questions to scaffold PTs learning and engage them in mathematical processes such as making conjectures, justifying their reasoning, and proving or disproving conjectures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Learning to Teach Mathematics Through Problem Solving

Judy Bailey

What problem-solving knowledge is required in mathematical teaching? A curricular approach

Juan Luis Piñeiro, Elena Castro-Rodríguez & Enrique Castro

Mathematical Knowledge for Teaching Proof: Comparing Secondary Teachers, Pre-Service Secondary Teachers, and Undergraduate Majors

Orly Buchbinder, Sharon McCrone, … Rebecca Butler

Alderton, J. (2008). Exploring self-study to improve my practice as a mathematics teacher educator. Studying Teacher Education, 4 (2), 95–104.

Article   Google Scholar  

Ball, D. L., & Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J. Boaler (Ed.), Multiple perspectives on the teaching and learning of mathematics (pp. 83–104). Westport, CT: Ablex.

Google Scholar  

Ball, D. L., & Bass, H. (2003). Toward a practice-based theory of mathematical knowledge for teaching. In B. Davis & E. Simmt (Eds.), Proceedings of the 2002 annual meeting of the Canadian Mathematics Education Study Group (pp. 3–14). Edmonton, AB: CMESG/GCEDM.

Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it so special? Journal of Teacher Education, 59, 389–407.

Chapman, O. (2008). Mathematics teacher educators’ learning from research on their instructional practices: A cognitive perspective. In B. Jaworski & T. Wood (Eds.), The international handbook of mathematics teacher education: The mathematics teacher educator as a developing professional (Vol. 4, pp. 115–134). Rotterdam: Sense Publishers.

Cochran-Smith, M. (2003). Learning and unlearning: The education of teacher educators. Teaching and Teacher Education, 19, 5–28.

Cochran-Smith, M., & Lytle, S. (1999). Relationship of knowledge and practice: Teacher learning in communities. In A. Iran-Nejad & C. D. Pearson (Eds.), Review of research in education (Vol. 24, pp. 249–306). Washington, DC: AERA.

Conference Board of the Mathematical Sciences. (2001). The mathematical education of teachers . Washington, D.C.: American Mathematical Society.

Book   Google Scholar  

Conference Board of the Mathematical Sciences. (2012). The mathematical education of teachers II . Washington, D.C.: American Mathematical Society.

Corbin, J., & Strauss, A. (2008). Basics of qualitative research (3rd ed.). Thousand Oaks, CA: Sage Publications Inc.

Darling-Hammond, L., & Snyder, J. (2000). Authentic assessment for teaching in context. Teaching and Teacher Education, 16, 523–545.

Goodchild, S., Fuglestad, A. D., & Jaworski, B. (2013). Critical alignment in inquiry-based practice in developing mathematics teaching. Educational Studies in Mathematics, 84, 393–412.

Goodell, J. (2011). Reforming mathematics teacher education through self-study. In S. Schuck & P. Pereria (Eds.), What counts in teaching mathematics? Adding value to self and content (pp. 111–125). Dordrecht: Springer.

Chapter   Google Scholar  

Grouws, D. A. (2003). The teacher’s role in teaching mathematics through problem solving. In H. L. Schoen (Ed.), Teaching mathematics through problem solving: Grades 6–12 (pp. 129–141). Reston, VA: National Council of Teachers of Mathematics.

Henningsen, M., & Stein, M. K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28 (5), 524–549.

Hiebert, J., & Wearne, D. (1993). Instructional tasks, classroom discourse, and student learning in second grade. American Educational Research Journal, 30, 393–425.

Hiebert, J., & Wearne, D. (2003). Developing understanding through problem solving. In H. L. Schoen (Ed.), Teaching mathematics through problem solving: Grades 6–12 (pp. 3–13). Reston, VA: National Council of Teachers of Mathematics.

Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42, 371–406.

Jansen, A., Bartell, T., & Berk, D. (2009). The role of learning goals in building a knowledge base for elementary mathematics teacher education. The Elementary School Journal, 109 (5), 525–536.

Lesh, R., & Zawojewski, J. (2007). Problem solving and modeling. In F. K. Lester Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 763–804). Charlotte, NC: Information Age Publishing.

Lobato, J., Clarke, D., & Ellis, A. B. (2005). Initiating and eliciting in teaching: A reformulation of teaching. Journal for Research in Mathematics Education, 36 (2), 101–136.

Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States . Mahwah, NJ: Lawrence Erlbaum.

Marcus, R., & Fey, J. T. (2003). Selecting quality tasks for problem-based teaching. In H. L. Schoen (Ed.), Teaching mathematics through problem solving: Grades 6–12 (pp. 55–67). Reston, VA: National Council of Teachers of Mathematics.

Masingila, J. O., Lester, F. K., & Raymond, A. M. (2011a). Mathematics for elementary teachers via problem solving: Instructor resource manual (3rd ed.). Acton, MA: Copley Custom Textbooks.

Masingila, J. O., Lester, F. K., & Raymond, A. M. (2011b). Mathematics for elementary teachers via problem solving: Student activity manual (3rd ed.). Acton, MA: Copley Custom Textbooks.

Masingila, J. O., Olanoff, D. E., & Kwaka, D. K. (2012). Who teaches mathematics content courses for prospective elementary teachers in the United States? Results of a national survey. Journal of Mathematics Teacher Education, 15 (5), 347–358.

McCrory, R., Zhang, C., Francis, A. P., & Young, S. (2009). Factors in the achievement of elementary teachers in mathematics classes. In S. L. Swars, D. W. Stinson & S. Lemons-Smith (Eds.), Proceedings of the 31st annual meeting of the North American chapter of the international group for the psychology of mathematics education (Vol. 5, pp. 1179–1187). Atlanta, GA: Georgia State University.

Polya, G. (1957). How to solve it (2nd ed.). Princeton, NJ: Princeton University Press.

Schön, D. (1983). The reflective practitioner . London: Temple Smith.

Schorr, R. Y., & Koellner-Clark, K. (2003). Using a modeling approach to analyze the ways in which teachers consider new ways to teach mathematics. Mathematical Thinking and Learning, 5 (2–3), 191–210.

Schroeder, T. L., & Lester, F. K. (1989). Developing understanding in mathematics via problem solving. In P. R. Trafton & A. P. Shulte (Eds.), New directions for elementary school mathematics (pp. 31–42). Reston, VA: National Council of Teachers of Mathematics.

Schuck, S., & Pereira, P. (2011). What counts in mathematics education. In S. Schuck & P. Pereira (Eds.), What counts in teaching mathematics? Adding value to self and content (pp. 1–9). Dordrecht: Springer.

Simon, M. A. (2000). Research on the development of mathematics teachers: The teacher development experiment. In A. E. Kelly & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education . Mahwah, NJ: Lawrence Erlbaum.

Smith, K. (2003). So, what about the professional development of teacher educators? European Journal of Teacher Education, 26 (2), 201–215.

Stanic, G. M. A., & Kilpatrick, J. (1989). Historical perspectives on problem solving in the mathematics curriculum. In R. I. Charles & E. A. Silver (Eds.), The teaching and assessing of mathematical problem solving (pp. 1–22). Reston, VA: National Council of Teachers of Mathematics.

Stein, M. K., Boaler, J., & Silver, E. A. (2003). Teaching mathematics through problem solving: Research perspectives. In H. L. Schoen & R. I. Charles (Eds.), Teaching mathematics through problem solving: Grades 6–12 . Reston, VA: National Council of Teachers of Mathematics.

Stein, M. K., Grover, B. W., & Henningsen, M. (1996). Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. American Educational Research Journal, 33 (2), 455–488.

Stein, M. K., & Smith, M. S. (1998). Mathematical tasks as a framework for reflection: From research to practice. Mathematics Teaching in the Middle School, 3 (4), 268–275.

Tzur, R. (2001). Becoming a mathematics teacher-educator: Conceptualizing the terrain through self-reflective analysis. Journal of Mathematics Teacher Education, 4 (4), 259–283.

Wenger, E. (1998). Communities of practice . Cambridge, UK: Cambridge University Press.

Wilson, P., Sztajn, P., Edgington, C., & Confrey, J. (2014). Teachers’ use of their mathematical knowledge of teaching in learning a mathematics learning trajectory. Journal of Mathematics Teacher Education, 17 (2), 149–175.

Zaslavsky, O. (2005). Seizing the opportunity to create uncertainty in learning mathematics. Educational Studies in Mathematics, 60, 297–321.

Zaslavsky, O. (2007). Mathematics-related tasks, teacher education and teacher educators. Journal of Mathematics Teacher Education, 10, 433–440.

Zaslavsky, O. (2008). Meeting the challenges of mathematics teacher education through design and use of tasks that facilitate teacher learning. In B. Jaworski & T. Wood (Eds.), The international handbook of mathematics teacher education: The mathematics teacher educator as a developing professional (Vol. 4, pp. 93–114). Rotterdam: Sense Publishers.

Zaslavsky, O., & Leikin, R. (2004). Professional development of mathematics teacher educators: Growth in practice. Journal of Mathematics Teacher Education, 7, 5–23.

Zopf, D. (2010). Mathematical knowledge for teaching teachers: The mathematical work of and knowledge entailed by teacher education . Unpublished doctoral dissertation. Retrieved from http://deepblue.lib.umich.edu/bitstream/handle/2027.42/77702/dzopf_1.pdf .

Download references

Author information

Authors and affiliations.

Syracuse University, 230 Huntington Hall, Syracuse, NY, 13244, USA

Joanna O. Masingila

Widener University, Chester, PA, USA

Dana Olanoff

Glendale Community College, Glendale, AZ, USA

Patrick M. Kimani

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Joanna O. Masingila .

Appendix: Code definitions

Curriculum and sequencing: reference to course textbooks and sequencing.

Materials: reference to mathematics manipulatives.

Pedagogical decisions: instructional decisions (“decide” should be explicit or implicit).

Mathematical ideas: mathematics content.

Instructor wonderings: evidence of instructor wondering (“wonder” should be explicit or implicit).

Instructor learning: connections or deepening understanding made by the instructor.

Instructor facilitating: actions instructor makes to facilitate learning.

Instructor planning: actions that instructor plans or planned to do.

Instructor struggles: struggles of instructor.

Instructor attitudes: attitudes displayed or articulated by instructor.

Instructor expectations: expectations instructor has about PTs and/or material.

Instructor goals: goals instructor has.

Instructor engagement: references to engagement or lack thereof by instructor.

Reflection in action: reflecting in the act of teaching.

Reflection on action: reflecting on teaching action.

Reflection on action of others: reflecting on teaching action of others.

Student wondering: observations of PTs wondering (“wonder” should be explicit or implicit).

Student learning: connections or deepening understanding made by student(s).

Student facilitating: actions student makes to facilitate learning.

Student struggles: struggles of student(s).

Student attitudes: attitudes displayed or articulated by student(s).

Student expectations: expectations student has about material, instructor, course, or related objects.

Student engagement: references to engagement or lack thereof by PTs.

Rights and permissions

Reprints and permissions

About this article

Masingila, J.O., Olanoff, D. & Kimani, P.M. Mathematical knowledge for teaching teachers: knowledge used and developed by mathematics teacher educators in learning to teach via problem solving. J Math Teacher Educ 21 , 429–450 (2018). https://doi.org/10.1007/s10857-017-9389-8

Download citation

Published : 27 October 2017

Issue Date : October 2018

DOI : https://doi.org/10.1007/s10857-017-9389-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Mathematical knowledge for teaching teachers
• Mathematical knowledge for teaching
• Teaching via problem solving
• Community of practice
• Inquiry as stance
• Primary mathematics teachers
• Elementary mathematics teachers
• Find a journal
• Publish with us
• Track your research

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Brief research report article, game-based learning experiences in primary mathematics education.

• Department of Economics, Faculty of Economics and Social Science, Partium Christian University, Oradea, Romania

Using game-based learning (GBL), especially digital game-based learning (DGBL), as a teaching and learning environment can be a pedagogical resource and a good strategy in the classroom to support mathematical learning. Effective manipulatives and games play a crucial role in promoting mathematical understanding. They support students in building, reinforcing and connecting varied representations of mathematical concepts. High-quality games are particularly valuable for learners as they provide them with control and adaptability. These games have properties that are adapted to cognitive and mathematical structures, facilitating the development of connections between different pieces and forms of knowledge. Digital games can help to achieve the same effects. In this paper, we conduct a quasi-experiment using games developed for this purpose. Our aim is to investigate whether non-digital games vs. digital games yield different results. Our results indicate that while students enjoyed themselves and found the task-solving enjoyable during both types of game-based learning, the use of non-digital games vs. digital games can sometimes lead to different outcomes.

1 Introduction

According to Rosli et al. (2015) prekindergarten, kindergarten, and elementary school teachers use both tangible and virtual manipulatives as instructional aides to facilitate student understanding of concepts in numbers, operations, geometry, algebra, measurements, data analysis, and probability. Tangible manipulatives assist students in constructing, reinforcing, and linking diverse mathematical concepts. From literature, engaging in concrete activities serves as a beneficial mental exercise ( Clements, 1989 ; Kamii, 1989 ). Clements (1999) found that for teachers to actively engage children's thinking, manipulatives must be integrated into educational tasks to provide meaningful context and support, alone they are not enough. “Games are effective not because of what they are, but because of what they embody and what learners are doing as they play a game” ( Van Eck, 2006 , p. 18). According to Russo and Russo (2018) and Russo et al. (2023) , the six principles of educationally rich mathematical games in the literature are: 1. Students are engaged; 2. There is a balance of skill and luck. 3. Mathematics is central. 4. Flexibility in learning and teaching. 5. Promotes home-school connections. 6. Games into studies. The educational value of a game depends on the extent to which teachers perceive that a game is appropriately challenging, engaging, enjoyable, adaptable to support different learners, and adaptable to inquiry or broader mathematical investigations. Likewise, perceived levels of student enjoyment and engagement, as well as the potential of a game leads to rich mathematical inquiry, were important features in assessing how likely a teacher would be using a particular game with students in the future if given the opportunity, as was the game's ability to support mathematical discussion. Research by Bordás (2016) shows that in order to motivate students and adapt to their individual needs, teachers at both lower and upper secondary level consider it important to use interactive methods, game-based teaching and the use of the internet and digital tools.

In practice, primary school teachers tend to use non-digital mathematical games to support maths learning (board, dice, and card games). According to Russo and Russo (2020) and Russo et al. (2021) almost all the primary teachers admitted playing mathematical games in their classrooms a minimum of once a week, they view games as highly effective for developing all four proficiencies highlighted in the Mathematics Curriculum: fluency, understanding, problem-solving, and reasoning. According to Dienes (2015) , activities, games and concrete experiences should be the base of learning mathematics, that could be a joyful experience with the use of tools that enhance efficiency. In primary school, children establish connections between abstract concepts and practical experiences in a more tangible manner, experiencing them through games. Manipulatives are “objects designed to represent explicitly and concretely mathematical ideas that are abstract” ( Moyer, 2001 , p. 176). Rosli et al. (2015) said that manipulatives help students to see the connections between concepts and improve their knowledge in problem solving and problem posing, even in the case of real-life problems. The incorporation of games serves as a compelling tool in the process of learning mathematics. Di Sia (2017) found that the association with games stimulates children's imagination, providing an enjoyable approach to mathematics, that is perceived as a helpful and enjoyable discipline. Students enjoy the tasks, where they have to invest mental effort in the use of games, didactic materials ( Yung and Paas, 2015 ).

The virtual tool does not seem suitable for this. Öztop (2022) examining the impact of using games in primary school mathematics education on learning outcomes and comparing effect sizes by game type finds that the effect of digital games is small (0.436) and that of non-digital games is large (1.032). The results show that non-digital games are much more effective on learning outcomes than digital games in primary school mathematics education.

According to the literature, there is a contrast between the frequency that teachers prefer to use non-digital games with students vis-a-vis the tendency in the literature to focus on digital games, where the majority of research focused on game-based learning in mathematics, specifically tend to explicitly focus on digital games, rather than non-digital games ( Hainey et al., 2016 ; Hussein et al., 2022 ). The large scale of quantitative studies involving non-digital games are comparatively rare, with most studies into games occurring within a single school context, generally involving students from a limited range of specific grade levels.

Guiding the pedagogical practice of teacher trainees as their supervisor, we created our own development games and we implemented together with the students in classrooms where they teach, and then we examined the experiences and results together. Our question is: whether non-digital games vs. digital games are different?

2 Digital games, digital game-based learning and achievements in learning of mathematics

According to the literature, numerous studies have identified positive impacts associated with the use of games in learning mathematics ( Suh et al., 2005 ; Steen et al., 2006 ; Moyer-Packenham et al., 2008 ). Such activities are typically interactive, motivating, and practical, contributing to maintaining students' interest and enhancing their understanding of mathematical concepts. The aim is to integrate games into the educational environment to enhance students' mathematical learning, expanding the use of games based on higher-order thinking can diversify the educational benefits of games and serve a wider range of learning objectives. Kailani et al. (2019) found that the games, by themselves, do not automatically imply positive impact. One must consider the diverse factors that work in tandem with game-based learning. Such factors include the technical aptitude and attitudes of the people—classroom teachers, faculty members, parents, and researchers—implementing the technology. Not only should there be an effective implementation plan that is well-executed, but the content of that execution needs to be well-designed with thorough curricula relevance.

Game-based learning means the use of games for educative purposes and aimed to improve the user knowledge and experience. The main benefit of these educational games is they focus on improving children's life-essential abilities such as problem solving and critical thinking. GBL aimed to improve the user's knowledge and experience.

Digital game-based learning (DGBL) is learning by using certain computer games for educational purposes. It is a type of game-based learning (GBL; Prensky, 2001 ). Computer games can be used as a “learning tool” ( Ke, 2008 , p. 1609) that “simulate real-life social networks” ( Neville et al., 2009 , p. 410; Ferguson, 2014 ) and motivational situations such as the use of real-world and computer-generated data to perform math operations.

The contemporary epistemological and pedagogical viewpoints in mathematical education highlight the importance of incorporating realistic mathematical practices and sense-making experiences. Problem solving is a major component of “thinking mathematically” ( Schoenfeld, 2020 ). A DGBL activity engages students in the process of problem solving or knowledge acquisition when facing the challenges presented by the game ( Huang et al., 2010 ). Literature suggests that DGBL stands out as a promising approach for enhancing students' learning motivation and achievement in mathematics. The computer games in terms of being interactive, based on a set of agreed rules and constraints, and directed toward a clear goal and constantly provide feedback, either as a score, toenable players to monitor their progress toward the goal ( Clark et al., 2016 ) DGBL demonstrates positive impacts on learning across diverse subjects and for various types of learners. Its motivational aspect significantly engages and captivates learners. Additionally, DGBL actively supports, reinforces, and expedites the learning process, contributing to the development of higher-order cognitive skills ( Hong et al., 2009 ). “The game playing process therefore supports the learning process by allowing players to acquire learning experiences in games, encouraging interactions between learners and the game system, and situating learners in complex learning environments” ( Huang, 2011 , p. 694). Twigg (2011) emphasized the essential integration of technology into mathematics curriculum, asserting its necessity for student learning in contemporary society. Accordingly, the utilization of interactive software and computers emerges as crucial tools in facilitating math learning through practical engagement. Ferguson (2014) found that DGBL can offer students the opportunity to enhance their current knowledge when teachers provide the right DGBL environment relevant to the curriculum being learned. Hung et al. (2014) stated that supplying practice opportunities along with immediate feedback through the use of computer and information technologies proves to be effective in encouraging students to enhance their understanding of mathematics.

Teed (2012) asserts that DGBL or GBL unfolds within a virtual environment enriched with fantasy elements, involving participants in educational activities through the utilization of technological tools like computers. DGBL specifically employs digital games to instigate competition, captivate learners, and provide challenges, ultimately serving as a motivational and engaging medium for learning.

Trybus (2015) claims that GBL has many advantages. It offers cost-effectiveness, minimal physical risk or liability to learners, standardized assessments for facilitating student-to-student comparisons, high levels of engagement, a learning pace customized to individual student needs, immediate feedback responses to errors, seamless transfer of learning to real-world scenarios, and an overall engaging experience for the learner.

Gillispie et al. (2010) observed that students exhibited an average increase of 17% in math achievement when 500 middle school students were examined regarding their achievement and attitudes while using problem-based digital games that incorporated concepts in prealgebra and algebra. The study found that students were not only receptive to repeating GBL missions but were also willing to engage in them to enhance their scores on the computer.

In a quantitative study ( Roschelle et al., 2010 ) the aim was to assess whether the utilization of computer software led to increased student engagement in mathematics class and enhanced learning for fourth-grade students. The results indicated that students in the experimental group, those exposed to the computer software, achieved higher scores on the post-test compared to students in the control group. In a mixed-methods study, Sardone and Devlin-Scherer (2010) involving 25 undergraduate students in teacher education to identify twenty-first-century skills utilized in educational games. The participants evaluated 50 games based on specific criteria such as motivation, critical thinking, problem-solving, collaboration, and communication. The findings revealed that digital games inherently incorporate many of these twenty-first-century skills. Ke (2008) identified that game design plays a crucial role in shaping students' interaction with the game.

In their meta-analysis, Li and Ma (2010) explored the impact of computer technology on the learning of mathematics in kindergarten through 12th grade students. Their findings revealed a generally positive correlation between students' academic achievement and the utilization of GBL, particularly among special needs students, elementary students, and those in a constructivism classroom setting.

Several studies have examined the effects of GBL teaching method on students' achievements, emphasizing the significance of its effects on the development of students' affective domain, which is closely linked to the subject and its instruction. A systematic review by Divjak and Tomic (2011) of 27 studies identified from the years 1995 to 2010, focusing on game-based learning (GBL) in mathematics education. Their findings indicated that math learning games not only facilitated the achievement of specific learning objectives but also enhanced students' motivation and fostered positive attitudes toward learning mathematics.

In a one-shot case study ( Khan and Chishti, 2011 ) the objective was to examine the impact of students' active participation on math achievement. Employing a posttest-only design, the study revealed a significant correlation, indicating that students' active engagement in math class had a considerable influence on their math achievement. In his study Ferguson (2014) presented statistical significance for the use of traditional mathematics teaching methods over the use of DGBL in combination with traditional mathematics teaching methods.

Wouters et al. (2013) found that serious games were more effective than conventional instruction in terms of learning and retention, but found no evidence that they were more motivating.

Clark et al. (2016) suggests that game environments support overall improvements in intrapersonal learning outcomes compared to non-game educational environments, and that game designers and educational researchers should collaborate on designs to keep game graphics, environments, and narratives optimally aligned with assessed learning objectives. In an action research study ( White and McCoy, 2019 ) which explored game-based learning as fifth grade mathematics students utilizing game-based lessons, results revealed that student attitudes improved both toward the lessons and toward math in general. Indriani et al. (2019) aimed to describe the quality of problem based learning assisted by Monopoly games on students critical thinking skill for seventh grade students shows that implementation PBL assisted by Monopoly game improve the students' mathematical critical thinking skills.

The results of a systematic review ( Vankúš, 2021 ) with the use of 57 journals, indicate that 54% of the articles consider the affective domain in the measurement of the effects of game-based learning in mathematics education. These articles report mostly (84%) the positive influences of game-based learning on students' motivation, engagement, attitudes, enjoyment, and state of flow.

Manzano-León et al. (2021) in their systematic review in three multidisciplinary databases, on quantitative experimental studies that explore the impact of educational gamification on student motivation and academic performance in the last 5 years (40 studies), most of them report gamification as a valid learning strategy and the results support the conclusion that educational games have a potential impact on the academic performance, commitment, and motivation of students.

Erşen and Ergül (2022) analyzed 80 research studies conducted between 2017 and 2021 on games and mathematical teaching using qualitative methods. As a result, studies aimed at determining effect gained importance, and in the methodological context, quantitative studies were frequently preferred and experimental designs were used accordingly. It was also found that secondary school students were preferred as participants, that the most common type of game used was digital computer games, that the games were mostly associated with the learning area of “numbers and operations,” and that the research studies had mostly positive results for the use of games in mathematics education.

According to Pan et al. (2022) , in the recent decade, over 20 major literature reviews have explored the effects of learning games on students' performances, only six of these reviews focused on mathematical education. Mathematics educators generally agree that teaching and learning mathematics requires different skills compared to other subject matters. As such, games designed and employed for mathematics education can differ from those for other subject matters.

In a quantitative meta-analysis review of 24 studies, Tokac et al. (2019) investigated the effects of learning video games on mathematics achievement of PreK-12th grade students compared to traditional classroom methods. Results showed heterogeneity among effect sizes, both in magnitude and direction and suggested that mathematics video games contributed to higher learning gains as compared to traditional instructional methods.

Kailani et al. (2019) in a sistematic review of the literature found that in 12 out of the 14 studies had participants from the age group of 6–14, while two studies had a sample population of undergraduate students between the ages of 17–20. The focus of research on games is mainly in the early years of primary school, as games are rarely used in secondary school mathematics and with university students.

3 Research methodology

Our aim is to investigate whether non-digital games vs. digital games yield different results. Our research was based on three mathematical games. Random sampling was used: a group of students used non-digital (card-based) games, the other group used a DGBL test on computers in the informatics lab. All participants worked an hour and were supervised during the test by us. Participation in the experiment was voluntary. For the elementary school students, the teacher requested parental consent, and all of them agreed.

3.1 Participants

The data was collected in 2022 and 103 individuals, 9–11-year-old elementary school students participated from three schools in Western Region of Romania. Distribution of elementary students according to methods: 49 students (47.57%) used DGBL and 54 (52.42%) used non-digital games.

3.2 Instrument

In the literature we found that majority of teachers prefer arithmetic operations with numbers focused games in their classes. Therefore, we wanted to choose a less used area (e.g., measurement and logic).

The games designed by us could be classified to different mathematical content areas: 1st problem: focuses on numbers, logic, strategy; 2nd problem: geometry, strategy, and measurement, 3rd problem: propositional logic and reasoning.

The universal online platform that was used for the DGBL test was created within JavaScript, PHP, HTML, and CSS, which made screenshots of the final solutions. As non-digital games we used different paper cards. For assessment we analyzed the screenshots. The maximum points the participants could reach was 100 for each problem. Once students clicked the “Completed” button, the solution was saved in the database as screenshots. Participants also had the option to use the “Start “gain” button.

Our research tool included the following tasks:

1. The hexagon problem ( Figure 1 ). Place the small hexagons into the large shape so that adjacent triangles contain the same number (triangles are considered adjacent if they share a side). The hexagons cannot be rotated ( Marchis, 2013 , p. 64).

2. The cake problem ( Figure 2 ). The figure represents a lattice cake consisting of 20 equal- size squares. Five friends wish to share the cake in such manner that each of them gets a differently shaped four-square piece. Could you help them out? ( Matlap, 2018a , p. 308).

3. The house problem ( Figure 3 ). There are five houses in five different colors. Each house is inhabited by a person of a different nationality. Each owner prefers a certain beverage, has a different hobby and keeps a certain pet. No owner drinks the same beverage, has the same pet, or has the same hobby as their neighbor. What we know is:

1. The British lives in a red house.

2. The Swedish has a dog.

3. The Danish drinks tea.

4. The German plays the piano.

5. The Norwegian lives in the first house.

6. The green house's owner drinks coffee.

7. The owner who plays golf likes juice.

8. The owner of the yellow house plays football in his free time.

9. The owner who dances has a parrot.

10. The man who lives in the middle house drinks tea.

11. The owner who plays board games lives next to the one that has a cat.

12. The man who has a horse, lives next to the one who plays football.

13. The Norwegian lives next to the blue house.

14. The owner who plays board games is the neighbor of the one who drinks water.

15. The green house is next to the white house, on the left.

Figure 1 . The hexagon problem.

Figure 2 . The correct solution of the cake problem ( Matlap, 2018b , p. 384).

Figure 3 . The solution for the house problem.

Who owns the fish? ( Székely, 2012 , p. 53). The problems and their solutions can be found in the Supplementary file .

3.3 Hypotheses

The research questions of the study is: whether non-digital games vs. digital games are different? The assigned null hypothesis was as follows: H0: There will be no statistically significant difference in student achievement between students assessed with non-digital games and students assessed with digital games.

4.1 Results of the first problem

The first task was to arrange seven hexagon-shaped pieces in accordance with specific rules. Various strategies can be employed to solve this problem; participants may attempt to locate the middle piece, initiate the arrangement from the sides, or employ trial-and-error methods. Despite placing significant emphasis on carefully reading and following the rules, many students, including undergraduates, failed to adhere to the instructions (e.g., they want to rotate pieces).

Majority of participants, 61 individuals (59.22%), successfully solved the problem, while 42 participants (40.77%) did not.

Among the elementary school students who worked with cards (54 students), 18 students (33.33%) successfully solved the problem, while two-thirds (36 students, 66.66%), were unsuccessful. On the other hand, of the elementary school students engaged in DGBL, a substantial majority (43 students, 87.76%), solved the problem, only six students (12.24%) failed. There was a significant difference in achievement between digital games and cards for elementary school students, as indicated by the statistical analysis [ t (103) = 6.67, p < 0.05].

The Table 1 shows the results.

Table 1 . Results of the first problem.

4.2 Results of the second problem

The second problem serves as a prime example of manipulating plane shapes, with only one correct solution. Nearly all participants correctly interpreted the problem, but the challenge lay in finding the perfect solution. The task required participants to put five different shapes into the grid, essentially cutting the “cake” into five pieces. Consequently, the maximum score was 5, which was transformed into a percentage. For instance, achieving 5/5 corresponded to 100%, 4/5 to 80%, and so forth. The detailed results are presented in Table 2 , revealing that the majority (76 students, 73.78%) achieved scores between 60 and 80%.

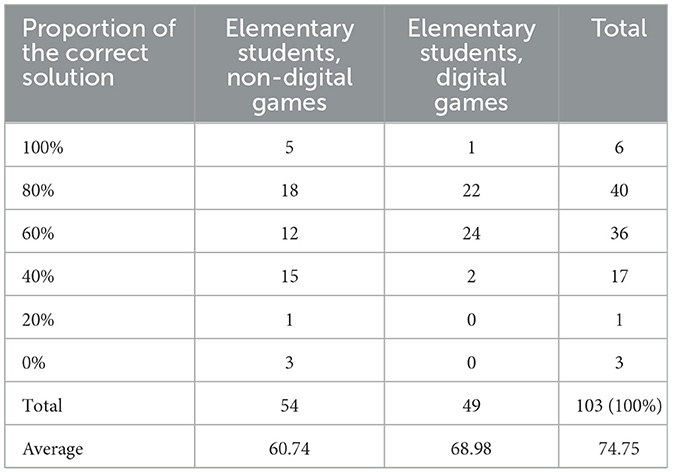
Table 2 . Results of the second problem.

Table 2 also indicates that perfect results were attained by six elementary students: five working with non- digital games (9.25%) and one student with DGBL (2.04%). In comparison of the averages presented in Table 2 , with F -tests and t -tests applied, the results achieved by the two groups of elementary school students are significantly different: DGBL solvers outperformed non-digital solvers, as indicated by t (103) = 2.08, p < 0.05.

4.3 Results of the third problem

The final task involved a logic puzzle that measured propositional logic thinking. There are five houses of different colors next to each other and houses have to arranged in a particular order. Only two participants (1.94%) successfully solved the problem, while 6 (5.82%) either failed or gave up. The remaining students demonstrated varying degrees of success in solving the problem. Some students who use non-digital game, employed interesting problem-solving methods, such as placing cards in a chart, while others used the floor space, stating the need for more room to process the task.

Table 3 provides detailed data on the results obtained by the groups of participants, revealing that 89.32% of them (92 students) achieved < 50%.

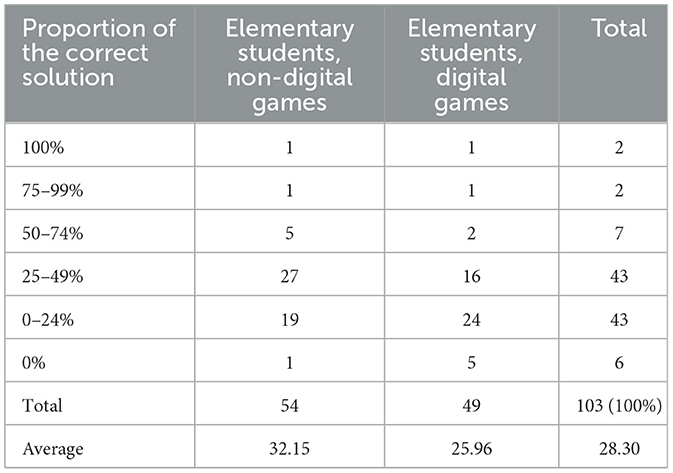
Table 3 . Results of the third problem.

5 Discussion

In our experiment two different groups was tested: a group of students used non-digital (card-based) games, the other group used a DGBL test. The large scale quantitative studies involving non-digital games are comparatively rare, in our case majority, 54 participants use non-digital games (52.42% of students involved).

The games designed by us could be classified to different content areas: numbers, geometry, strategy and measurement, propositional logic, and reasoning. These tasks are problem-type, hence more challenging, from a topic that is encountered less frequently and can be solved by elementary school students. However, when designing the games, it was possible to represent them in a plane, which is why we chose these.

The hypothesis: there will be no statistically significant difference in student achievement between students assessed with non-digital games and students assessed with digital games.

In case of the first problem: elementary school students demonstrated better results with DGBL, 43 students (87.76%) solved the problem. With non-digital games 18 elementary students (33.33%) solved the problem. There is a significant difference in achievement between digital and non-digital games for elementary school students, as indicated by the statistical analysis [ t (103) = 6.67, p < 0.05]. In their case, for this problem the digital game resulted in better solutions.

In case of the second problem, perfect results were attained by six elementary students: five working with non- digital games (9.25%) and one student with DGBL (2.04%). The average of elementary students who worked with non-digital games was 60.74, while for those who used digital games, the average was 68.98. There is a significant difference in the averages of the two groups of elementary school students: DGBL solvers outperformed non-digital solvers. In their case, the DGBL was the best game to resolve the problem.

In case of the third problem: two participants (1.94%) solved the problem, 89.32% (92 students) achieved < 50%, while 6 (5.82%) either failed or gave up. The average of elementary students who worked with non-digital games was 32.15, while for those who used digital games, the average was 25.96. F -tests and t -tests were conducted on the achievements of the two groups of elementary students, revealing no significant difference: t (103) = 1.62, p < 0.05 between their achievements.

When solving the third problem, we observed the following about the way of thinking: young schoolchildren treated logical statements more rigidly (they considered them in sequence, one after the other, if they encountered an obstacle, they did not overturn their previous assumptions). We observed that young schoolchildren were not flexible; they thought strictly in sequence, not preferring any particular statements, and did not pair statements. Some students who use non-digital game, employed interesting problem-solving methods.

Consequently, it can be concluded that the hypothesis is not confirmed for the 1st and 2nd problem, in case of elementary students for these problems the digital games were more effective. In case of the 3rd problem the null hypothesis was confirmed, is no statistically significant difference in student achievement between students assessed with non-digital games and students assessed with digital games.

During the experiment, we noticed that most of the participants enjoyed working both with the cards and with the digital games. The games were useful in engaging students in solving tasks. We conclude that can be a difference between the performance of students using non-digital games vs. students assessed digital games, there are tasks for which digital games help the learner, enabling them to solve them more successfully. Our results indicate that while students enjoyed themselves and found the task-solving enjoyable during both types of game-based learning, the use of non-digital games vs. digital games can sometimes lead to different outcomes.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

Ethical approval was not required for the study involving humans in accordance with the local legislation and institutional requirements. Written informed consent for participation in the study was not required from the participants and/or their legal guardians/next of kin in accordance with the national legislation and the institutional requirements.

Author contributions

ED: Conceptualization, Data curation, Investigation, Methodology, Supervision, Visualization, Writing – original draft.

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The content of this manuscript has been presented in part at the 8th International Scientific Colloquium Mathematics and Children, Osijek, Croatia, May 28–29, 2021 ( Debrenti and Back, 2022 ). Visualization in the Teaching and Learning of Mathematics, 8th International Scientific Colloquium Mathematics and Children 2021, Osijek, Croatia, 28–29 May . The author would like to thank her student, Annamaria Back, who helped her in developing the research instrument and for her valuable support in the research.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1331312/full#supplementary-material

Bordás, A. (2016). A szituatív tanulás szerepe partiumi magyar pedagógusok szakmai fejlődésében. [The role of situational learning in the professional development of Hungarian teachers in Partium]. REGIO 24, 211–239. doi: 10.17355/rkkpt.v24i4.143

Crossref Full Text | Google Scholar

Clark, D. B., Tanner-Smith, E. E., and Killingsworth, S. S. (2016). Digital games, design, and learning. Rev. Educ. Res. 86, 79–122. doi: 10.3102/0034654315582065

Clements, D. H. (1989). Computers in Elementary Mathematics Education . Englewood Cliffs, NJ: Prentice-Hall.

Google Scholar

Clements, D. H. (1999). “Concrete” manipulatives, concrete ideas. Contempor. Iss. Early Childh . 1:45. doi: 10.2304/ciec.2000.1.1.7

Debrenti, E., and Back, A. (2022). “Visualization in the teaching and learning of mathematics,” in Advances in Research on Teaching Mathematics , eds Z. Kolar-Begovic, R. Kolar-Super, and A. Katalenic (Zagreb), 72–89.

Di Sia, P. (2017). Learning mathematics through games in primary school: an applicative path. Edutainment 1, 127–132. doi: 10.15503/edut.2016.1.127.133

Dienes, Z. P. (2015). Építsük fel a matematikát! (Budapest: Gondolat), 47.

Divjak, B., and Tomic, D. (2011). The impact of game-based learning on the achievement of learning goals and motivation for learning mathematics-literature review. J. Inform. Org. Sci . 35, 15–30.

Erşen, Z. B., and Ergül, E. (2022). Trends of game-based learning in mathematics education: a systematic review. Int. J. Contempor. Educ. Res. 9, 603–623. doi: 10.33200/ijcer.1109501

Ferguson, T. (2014). Mathematics Achievement with Digital Game-Based Learning in High School Algebra 1 Classes. Doctoral Dissertations and Projects , 794. Available online at: https://digitalcommons.liberty.edu/doctoral/794 (accessed January 14, 2024).

Gillispie, L., Martin, F., and Parker, M. A. (2010). Effects of a 3-D video game on middle school student achievement and attitude in mathematics. Electr. J. Math. Technol . 4, 68–79.

Hainey, T., Connolly, T. M., Boyle, E. A., Wilson, A., and Razak, A. (2016). A systematic literature review of games-based learning empirical evidence in primary education. Comput. Educ . 102, 202–223. doi: 10.1016/j.compedu.2016.09.001

Hong, J. C., Cheng, C. L., Hwang, M. Y., Lee, C. K., and Change, H. Y. (2009). Assessing the educational values of digital games. J. Comput. Assist. Learn. 25, 423–437. doi: 10.1111/j.1365-2729.2009.00319.x

Huang, W. H. (2011). Evaluating learners' motivational and cognitive processing in an online game-based learning environment. Comput. Hum. Behav . 27, 694–704. doi: 10.1016/j.chb.2010.07.021

Huang, W. H., Huang, W. Y., and Tschopp, J. (2010). Sustaining iterative game playing processes in DGBL: the relationship between motivational processing and outcome processing. Comput. Educ . 55, 789–797. doi: 10.1016/j.compedu.2010.03.011

Hung, C. M., Huang, I., and Hwang, G. J. (2014). Effects of digital game-based learning on students' self-efficacy, motivation, anxiety, and achievements in learning mathematics. J. Comput. Educ . 1, 151–166. doi: 10.1007/s40692-014-0008-8

Hussein, M. H., Ow, S. H., Elaish, M. M., and Jensen, E. O. (2022). Digital game-based learning in K-12 mathematics education: a systematic literature review. Educ. Inform. Technol . 27, 2859–2891. doi: 10.1007/s10639-021-10721-x

Indriani, M. N., Isnarto, I., and Mariani, S. (2019). The implementation of PBL (problem based learning) model assisted by monopoly game media in improving critical thinking ability and self confidence. J. Prim. Educ . 8, 200–208. doi: 10.15294/jpe.v8i2.25991

Kailani, S., Newton, R., and Pedersen, S. (2019). “Game-based learning and problem-solving skills: a systematic review of the literature,” in Conference Paper: EdMedia + Innovate Learning 2019 . Amsterdam.

Kamii, C. K. (1989). Young Children Continue to Reinvent Arithmetic: 2nd Grade. Implications of Piaget's Theory . New York, NY: Teachers College Press.

Ke, F. (2008). A case study of computer gaming for math: engaged learning from gameplay? Comput. Educ . 51, 1609–1620. doi: 10.1016/j.compedu.2008.03.003

Khan, S. B., and Chishti, S. H. (2011). Learners' errors: supporting learners for participating in mathematics classroom. Int. J. Acad. Res . 3, 656–659.

Li, Q., and Ma, X. (2010). A meta-analysis of the effects of computer technology on school students' mathematics learning. Educ. Psychol. Rev . 22, 215–243. doi: 10.1007/s10648-010-9125-8

Manzano-León, A., Camacho-Lazarraga, P., Guerrero, M. A., Guerrero-Puerta, L., Aguilar-Parra, J. M., Trigueros, R., et al. (2021). Between level up and game over: a systematic literature review of gamification in education. Sustainability 13:2247. doi: 10.3390/su13042247

Marchis, J. (2013). Matematika óvó- és tanítóképzős hallgatóknak [Mathematics for Kindergarten- and Elementary School Teachers] . Kolozsvár: Galaxia Guttenberg Press.

Matlap (2018a). XXII (8), Radó Ferenc Matematikamuvelo Társaság (Kolozsvár: Matlap), 308.

Matlap (2018b). XXII (10), Radó Ferenc Matematikamuvelo Társaság (Kolozsvár: Matlap), 384.

Moyer, P. (2001). Are we having fun yet? How teachers use manipulatives to teach mathematics. Educ. Stud. Math . 47, 175–197. doi: 10.1023/A:1014596316942

Moyer-Packenham, P. S., Salkind, G., and Bolyard, J. J. (2008). Virtual manipulatives used by K-8 teachers for mathematics instruction: considering mathematical, cognitive, and pedagogical fidelity. Contempor. Iss. Technol. Teach. Educ . 8, 202–218.

Neville, D. O., Shelton, B. E., and McInnis, B. (2009). Cybertext redux: using digital game-based learning to teach L2 vocabulary, reading, and culture. Comput. Assist. Lang. Learn . 22, 409–424. doi: 10.1080/09588220903345168

Öztop, F. (2022). Effectiveness of using digital and non-digital games in primary mathematics teaching: a meta-analysis study. Int. Prim. Educ. Res. J . 6, 65–80. doi: 10.31235/osf.io/bc7er

Pan, Y., Ke, F., and Xu, X. (2022). A systematic review of the role of learning games in fostering mathematics education in K-12 settings. Educ. Res. Rev . 36:100448. doi: 10.1016/j.edurev.2022.100448

Prensky, M. (2001). Digital natives, digital immigrants. On The Horizon 9, 1–6. doi: 10.1108/10748120110424816

Roschelle, J., Rafanan, K., Bhanot, R., Estrella, G., Penuel, B., Nussbaum, M., et al. (2010). Scaffolding group explanation and feedback with handheld technology: impact on students' mathematics learning. Educ. Technol. Res. Dev . 58, 399–419. doi: 10.1007/s11423-009-9142-9

Rosli, R., Goldsby, D., and Capraro, M. M. (2015). Using manipulatives in solving and posing mathematical problems. Creat. Educ . 6, 1718–1725. doi: 10.4236/ce.2015.616173

Russo, J., Bragg, L., and Russo, T. (2021). How primary teachers use games to support their teaching of mathematics. Int. Electr. J. Element. Educ . 13, 407–419. doi: 10.26822/iejee.2021.200

Russo, J., Bragg, L., Russo, T., and Minas, M. (2023). Identifying the characteristics of non-digital mathematical games most valued by educators. Educ. Sci . 13:30. doi: 10.3390/educsci13010030

Russo, J., and Russo, T. (2018). “What makes a 'good' mathematical game?,” in Proceedings of the 55th annual conference of the Mathematics Association of Victoria . Bundoora; Melbourne.

Russo, J., and Russo, T. (2020). Transforming mathematical games into investigations. Austr. Prim. Math. Classr . 25, 14–19. doi: 10.3316/aeipt.229363

Sardone, N. B., and Devlin-Scherer, R. (2010). Teacher candidate responses to digital games: 21st-century skills development. J. Res. Technol. Educ . 42, 409–425. doi: 10.1080/15391523.2010.10782558

Schoenfeld, A. H. (2020). Mathematical practices, in theory and practice. ZDM Math. Educ. 52, 1163–1175. doi: 10.1007/s11858-020-01162-w

Steen, K., Brooks, D., and Lyon, T. (2006). The impact of virtual manipulatives on first grade geometry instruction and learning. J. Comput. Math. Sci. Teach . 25, 373–391.

Suh, J., Moyer, P. S., and Heo, H. J. (2005). Examining technology uses in the classroom: developing fraction sense using virtual manipulative concept tutorials. J. Interact. Onl. Learn . 3, 1–20.

Székely, Z. (2012). Eszezo, agypörgeto feladványok [Mind Games -Brain Teasers] (Déva: Corvin Kiadó), 53.

Teed, R. (2012). Game-Based Learning . Carleton College. Available online at: http://serc.carleton.edu/introgeo/games/index.html (accessed January 18, 2024).

Tokac, U., Novak, E., and Thompson, C. G. (2019), Effects of game-based learning on students' mathematics achievement: a meta-analysis. J. Comput. Assist. Learn . 2019, 1–14. doi: 10.1111/jcal.12347

Trybus, J. (2015). Game-Based Learning: What It Is, Why It Works, and Where It's Going (Miami: New Media Institute). Available online at: https://www.google.com/search?client=safariandrls=enandq=Retrieved+from+http%3A%2F%2F%2F+game-based-learning–what-it-is-why-it-works-and-where-its-going.html&ie=UTF-8&oe=UTF-8 (accessed January 24, 2024).

Twigg, C. A. (2011). The Math Emporium: Higher Education's Silver Bullet. Change Magazine Higher Learn. 43, 25–34.

Van Eck, R. (2006). Digital game-based learning: it's not just the digital natives who are restless. Educause Rev . 41, 16–30.

Vankúš, P. (2021). Influence of game-based learning in mathematics education on students' affective domain: a systematic review. Mathematics 9:986. doi: 10.3390/math9090986

White, K., and McCoy, L. P. (2019). Effects of game-based learning on attitude and achievement in elementary mathematics. Networks 21, 1–20. doi: 10.4148/2470-6353.1259

Wouters, P., van Nimwegen, C., van Oostendorp, H., and van der Spek, E. D. (2013). A meta-analysis of the cognitive and motivational effects of serious games. J. Educ. Psychol . 105, 249–265. doi: 10.1037/a0031311

Yung, H. I., and Paas, F. (2015). Effects of computer-based visual representation on mathematics learning and cognitive load. Educ. Technol. Soc . 18, 70–77.

Keywords: game-based learning, digital game-based learning, digital games, non-digital games, STEM, manipulatives, concrete, virtual

Citation: Debrenti E (2024) Game-Based Learning experiences in primary mathematics education. Front. Educ. 9:1331312. doi: 10.3389/feduc.2024.1331312

Received: 31 October 2023; Accepted: 26 February 2024; Published: 08 March 2024.

Reviewed by:

Copyright © 2024 Debrenti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Edith Debrenti, debrenti.edit@partium.ro

This article is part of the Research Topic

STEM: Innovation on Teaching and Learning

10 best AI math solver tools for math problem-solving

Homework AI makes it easier for students to learn difficult subjects. Boost your assignment and exam grades with these best AI homework helpers.

• March 18, 2024

The traditional approach to learning involves acquiring knowledge through listening and observation.

However, professionally trained AI can better accommodate different learning styles and enhance comprehension by offering tailored, on-demand learning assistance, especially in challenging subjects like mathematics.

As a subject many students struggle with, having access to a reliable AI math solver is invaluable. Math AI solvers can provide students and other learners with instant homework help outside the classroom at any time when needed.

They can also help improve students’ math test scores and build their mathematical skills over time. Let’s look at some of the best math AI tools for mathematical problem-solving:

Ten best AI math solver tools

1. Mathful – Best AI math solver overall

2. HIX Tutor – Best AI math solver for rapid homework response

3. AI Math – Best AI math solver for increasing math test scores

4. HomeworkAI – Best AI math solver for 24/7 math homework help

5. GeniusTutor – Best AI math solver for high-level learning 

6. Mathway – Best AI math solver for solving algebra problems

7. Air Math – Best AI math solver for mobile uses

8. StudyMonkey – Best AI math solver for in-depth explanations 

9. Interactive Mathematics – Best AI math solver for comprehensive chat support

10. Smodin – Best AI math solver for step-by-step solutions

Mathful – Best AI math solver overall

Mathful is an AI-powered math homework solver that provides step-by-step answers to all types of math questions.

The math AI tool uses a large language model and advanced algorithms to help students improve their math grades and prepare for exams.

Mathful has proven to be one of the most accurate AI math solvers, boasting a remarkable 98% accuracy rate across various mathematical disciplines, such as calculus, algebra, and geometry.

Mathful can also help students of all levels, from elementary school to university and beyond.

Mathful can help students improve their math grades in school by enforcing core math concepts and providing detailed explanations that promote comprehension.

Students can start using Mathful for free; low-cost subscription plans are available after the initial trial. 

• Able to provide highly accurate solutions and comprehensive explanations.
• Can process text and image files.
• Able to solve a variety of question types. 
• Available to use 24/7. 
• It cannot replace a real classroom education. 

Get instant answers to Math homework questions with Mathful AI math solver >>>

HIX Tutor – Best AI math solver for rapid homework response

HIX Tutor is a powerful AI homework helper that provides comprehensive support in many subjects, such as chemistry, biology, and physics.

It also serves as a personal AI math tutor, helping students boost their math grades and overall academic success. 

To use HIX Tutor’s advanced math AI, type in a math problem or upload an image or document of the question.

The tool instantly generates a detailed explanation for each problem step, helping students understand the underlying math concepts. 

HIX Tutor’s AI math problem solver can help save users time spent struggling with complicated math assignments.

Try the AI math solver at no cost. Once you’ve reached your question limit, upgrade to an affordable monthly or annual plan.

• Delivers step-by-step solutions to math questions.
• Trained on a large math knowledge dataset. 
• Reduces time spent on math homework. 
• Requires payment after the initial trial. 
• Some students may only use the tool to get answers without learning. 

Streamline the math learning experience with HIX Tutor’s math AI solver >>>

AI Math – Best AI math solver for increasing math test scores

How you prepare for a math test can significantly impact your performance.

AI math solvers like AI Math help take the frustration out of studying by providing thorough explanations that teach students how to tackle similar math problems. 

The AI math problem solver generates answers to questions in under 10 seconds with a 99% accuracy rate.

AI Math supports over 30 languages so that students can get responses in their native language for better understanding.

Students who use AI Math to supplement their classroom education experience an increase in their math test scores of up to 35%. Starting with AI Math is free; subscriptions cost just a few dollars a month.

• Covers most branches of math, such as arithmetic and trigonometry.
• Walks students through the solution to facilitate understanding. 
• Can solve simple to complex math problems.
• Does not currently offer advanced math features. 

Choose AI Math and study for math tests in a smarter way >>>

HomeworkAI – Best AI math solver for 24/7 math homework help

Students often need help with homework outside of traditional school hours. AI math solver tools like HomeworkAI allow students to get comprehensive support round-the-clock.

Much like a personal tutor, HomeworkAI focuses on teaching students how to solve homework problems instead of simply giving answers. 

HomeworkAI can handle math problems with multiple solution methods, meaning a primary solution and possible alternative approaches.

It can also analyze textbook material with practice math questions to aid students’ studies. 

While HomeworkAI excels in helping students complete math assignments with high precision, this AI homework tool can also help students in other school subjects, such as biology, physics, chemistry, literature, and history.

Try HomeworkAI for free, or choose from a low-cost subscription plan for unlimited uses. 

• Allows students to work at their own pace at home. 
• User-friendly platform is easy to navigate. 
• It can help students excel in many subjects, including math.
• This may cause students to rely too much on online math-solving platforms. 
• Rarely, solutions may be outdated or incorrect. 

Try HomeworkAI and get instant help for your math homework >>>

5. Genius Tutor – Best AI Math Solver for High-Level Learning

Genius Tutor is a versatile AI tutor and homework helper that can help students build their math skills and gain confidence in their academic abilities.

While the AI math solver is geared toward all types of learners, it is best suited for high school and college-level students.

The AI math problem solver provides a step-by-step breakdown for math questions of all types, showing the exact process of figuring out math problems and concepts.

Genius Tutor also highlights and explains important theorems, formulas, and rules so that students know when and how to use them.

Genius Tutor not only helps students complete math homework assignments in record time but can also help them prepare for exams.

No credit card is needed to try Genius Tutor, and budget-friendly paid subscriptions are available after the free trial.

• Can help students with all mathematical disciplines.
• Provides in-depth guides that foster lifelong learning. 
• Gives instant feedback on a variety of homework questions. 
• May not provide accurate solutions to highly complex math problems. 

Genius Tutor’s AI math solver can instantly elevate your math learning experience >>>

Mathway – Best AI math solver for solving algebra problems

Algebra is a complex branch of mathematics that many students struggle with in high school and college.

Mathway offers a sophisticated AI math solver designed to solve algebra homework questions, from word problems to complex mathematical operations that form meaningful expressions.

The math solver AI tool combines an algebra calculator with a conversational chatbot. Simply type in a math problem or upload a photo and get instant step-by-step solutions. 

Mathway also offers AI-driven math problem solvers for other branches of math, such as calculus, statistics, chemistry, and physics.

• The clean interface is easy to use. 
• You can upload documents on a computer or mobile device. 
• It makes it easy to master algebraic concepts. 
• Additional features require a paid upgrade. 
• Does not always provide detailed explanations. 

Air Math – Best AI math solver for mobile uses

Nowadays, many students rely on their smartphones or other mobile devices for homework help. Air Math is a smart AI math solver app available on Apple and Android devices.

Once installed, the Air Math app allows students to snap and solve math homework questions in under three seconds.

The innovative math AI solver can solve everything from geometry questions to word problems.

The 24/7 instant solutions include step-by-step solutions to teach students how to solve the problem independently. 

If you still have problems understanding the explanations, Air Math can connect you with professional math experts worldwide at any time. 

• Free to use.
• Offers support on mobile devices.
• You can ask expert math tutors for additional assistance. 
• Students can download the Chrome Extension on the web. 
• The app may not accurately read handwritten math questions. 

StudyMonkey – Best AI math solver for in-depth explanations 

StudyMonkey is a free AI homework helper that provides academic assistance in many areas, including mathematics.

The powerful AI math solver saves students time and headaches by instantly generating solutions to complex math problems, preventing long homework sessions. 

Type in the math problem, and StudyMonkey provides an accurate answer, detailed explanation, and steps to solve the problem to make it easier to understand.

This platform also retains a history of past questions asked, allowing students to review and revisit solutions anytime, aiding in effective long-term learning. 

• Can handle math problems from first grade to expert. 
• Offers a free plan. 
• Math features are limited.
• Can not upload images or documents. 
• You must pay for a subscription to ask more than three questions daily.

Interactive Mathematics – Best AI math solver for comprehensive chat support

Many students are familiar with chatbots, making Interactive Mathematics a popular option for homework help.

The state-of-the-art AI math problem solver claims to be more accurate than ChatGPT and more powerful than a math calculator. Its speed also surpasses human math tutors. 

Using Interactive Mathematics for homework help is also very simple.

You can type in your math question or upload an image, and the tool immediately sets to work, with the added benefit of offering solutions through a chatbot-style conversation that simulates a real-time, interactive math problem-solving session.

• You can help students improve their grades.
• Chat-based real-time problem-solving
• Offers bonuses like SAT/ACT prep courses. 
• Users can only ask three questions before reaching the free question limit.

Smodin – Best AI math solver for step-by-step solutions

The Smodin Math AI Homework Solver can help if you’re struggling with math homework.

This unique tool uses machine learning and AI algorithms to efficiently solve all types of math problems, from formulas to equations.

The tool also promises high accuracy, reducing the risk of submitting incorrect answers. 

Smodin doesn’t just provide a final answer to your query. It provides both brief answers and comprehensive explanations to help you better understand the concept.

It also shows a variety of relevant web answers and links to other resources, such as YouTube videos. 

• Users must make an account to start using Smodin.
• Step-by-step solutions are highly detailed and engaging. 
• Can help students ace their math exams. 
• Free users are limited to 3 daily credits. 
• Cannot upload images or documents. 

Final thoughts

Many students struggle with math, but that doesn’t mean they must settle for bad grades. With the right AI math solver, students can confidently develop their math skills and complete assignments and exams. 

Based on our assessments, Mathful easily stands out from the pack. It is a sophisticated AI math problem solver that offers enhanced problem-solving capabilities, accurate solutions, and affordable subscription plans.

Try Mathful for free and achieve greater academic success.

Have any thoughts on this? Drop us a line below in the comments, or carry the discussion to our  Twitter  or  Facebook .

Editors’ Recommendations:

MIGO Ascender vacuum is leading the future of robotic home cleaning

Neakasa M1 litter box – where performance meets purr-fection

Incogni vs Kanary: Who offers the better data removal service?

Disclosure: This is a sponsored post. However, our opinions, reviews, and other editorial content are not influenced by the sponsorship and remain objective .

Follow us on Flipboard, Google News, or Apple News

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Giveaway: Win the ultimate 420 experience with Grenco Science

Giveaway: Enter to win the HP Sprocket inkless photo printer

Save $170 on the Sony XM5 headphones – get yours today

Sam Bankman-Fried sentenced to 25 years for $8 billion fraud at FTX

Save $600 on Asus ROG Zephyrus G14 gaming laptop

Quick, score a pair of Beats Studio Buds+ for an unbelievable $99

Mint rival Quicken Simplifi is offering new customers 50% off

Buying Guide

The best steam deck accessories (2024).

How to view your Xbox library online

Quick, score 3 months of Xbox Game Pass Ultimate for just $26

Get lifetime access to Microsoft Office Pro for just $30

The best wireless earbuds (2024)

Here are the best STEM toys on the market today

Guy decides to explode his Tesla Model S instead of paying a $22.6K repair bill

The new Kirby and the Forgotten Land shows that the lovable pink ball will outlive us all

Uncategorized

This new ps5 game might be the most realistic looking game ever, tiktok wants to give you free money, more in sponsored.

Ascender, the pioneering robot vacuum and mop, effortlessly cleans entire homes with its unique...

The Neakasa M1 revolutionizes global cat care, providing cat owners with an unmatched user...

These popular data removal tools are often pitted against each other, boasting unique features...

EssayGPT Review: The Most Comprehensive AI Essay Writing Solution

Let's explore EssayGpt's impressive capabilities and how it revolutionizes essay writing through its suite...

EssayAI Review: Top Undetectable AI Essay Writer for Generating High-Quality Essays

EssayAI is an reputable undetectable AI essay writer that excels in generating high quality,...

EssayWriter Review: Best AI Essay Writer to Help You Write Better Essays

Wondering if EssayWriter is an ideal AI essay writer to create high-quality essays? Check...

EssayFlow is a cutting-edge undetectable AI essay writer

EssayFlow is an advanced AI essay writing assistant that not only produces essays but...

Mathful Review: Can This AI Math Solver Actually Solve Problems

In this article, we'll explore the key functionalities and the overall effectiveness of the...