assignment method algorithm always start by

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
• Introduction to Exact Cover Problem and Algorithm X
• Greedy Approximate Algorithm for Set Cover Problem
• Job Assignment Problem using Branch And Bound
• Implementation of Exhaustive Search Algorithm for Set Packing
• Channel Assignment Problem
• Chocolate Distribution Problem | Set 2
• Transportation Problem | Set 1 (Introduction)
• OLA Interview Experience | Set 11 ( For Internship)
• Top 20 Greedy Algorithms Interview Questions
• Job Sequencing Problem - Loss Minimization
• Prim's Algorithm (Simple Implementation for Adjacency Matrix Representation)
• Data Structures and Algorithms | Set 21
• Adobe Interview Experience | Set 55 (On-Campus Full Time for MTS profile)
• Amazon Interview Experience | Set 211 (On-Campus for Internship)
• OYO Rooms Interview Experience | Set 3 (For SDE-II, Gurgaon)
• C# Program for Dijkstra's shortest path algorithm | Greedy Algo-7
• Algorithms | Dynamic Programming | Question 7
• Amazon Interview | Set 46 (On-campus for Internship)
• Merge Sort - Data Structure and Algorithms Tutorials
• Must Do Coding Questions for Companies like Amazon, Microsoft, Adobe, ...
• QuickSort - Data Structure and Algorithm Tutorials
• Bubble Sort - Data Structure and Algorithm Tutorials
• Tree Traversal Techniques - Data Structure and Algorithm Tutorials
• Binary Search - Data Structure and Algorithm Tutorials
• Insertion Sort - Data Structure and Algorithm Tutorials
• Selection Sort – Data Structure and Algorithm Tutorials
• Understanding the basics of Linked List
• Breadth First Search or BFS for a Graph

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...

Similar reads.

• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

• Subtract the smallest entry in each row from all the entries of the row.
• Subtract the smallest entry in each column from all the entries of the column.
• Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
• Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

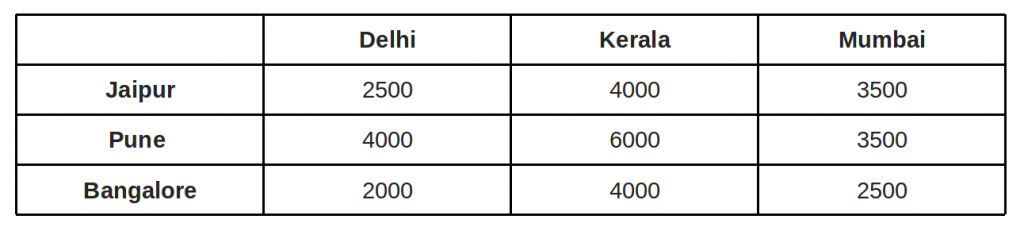
Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

• Emp 1 to Task 3
• Emp 2 to Task 2
• Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

Problem Formulation

A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.  

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

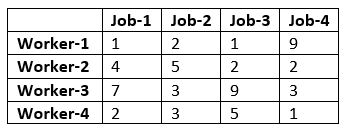
In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Blending Problem in Python using Gurobi
• Transshipment Problem in Python Using PuLP

You May Also Like

Agglomerative Clustering

apply() in Pandas

Working with Strings in Pandas

Assignment problem

1 formulation of the problem, 2 variants of the problem, 3 algorithms for solving the problem, 4 references.

Suppose that there are [math]n[/math] agents and [math]m[/math] tasks, which can be distributed between these agents. Only one task can be assigned to each agent, and each task can be assigned to only one agent. The cost of assignment of the [math]i[/math] -th task to the [math]j[/math] -th agent is [math]c(i, j)[/math] . If [math]c(i, j) = \infty[/math] , then the [math]i[/math] -th task cannot be assigned to the [math]j[/math] -th agent.

The assignment problem : find a feasible set of assignments [math]A = \{ (i_1, j_1), \ldots, (i_k, j_k) \}[/math] , [math]k = \min \{m, n\}[/math] having the maximum total cost:

If [math]m = n[/math] , then we say of the linear assignment problem : each agent is assigned to perform exactly one task, and each task is assigned to exactly one agent.

In the case of unit weights, we have to find a maximum matching in a bipartite graph, and the problem reduces to assigning as much tasks as possible.

• The Hungarian Method [1] [2] [3] for the linear problem. The complexity is [math]O(n^4)[/math] (and can be reduced [4] to [math]O(n^3)[/math] );
• the auction algorithm [5] [6] ;
• the Hopcroft-Karp algorithm [7] for the problem with unit weights. The complexity is [math]O(m \sqrt{n})[/math] .
• ↑ Kuhn, H W. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics Quarterly 2, no. 1 (March 1955): 83–97. doi:10.1002/nav.3800020109.
• ↑ Kuhn, H W. “Variants of the Hungarian Method for Assignment Problems.” Naval Research Logistics Quarterly 3, no. 4 (December 1956): 253–58. doi:10.1002/nav.3800030404.
• ↑ Munkres, James. “Algorithms for the Assignment and Transportation Problems.” Journal of the Society for Industrial and Applied Mathematics 5, no. 1 (March 1957): 32–38. doi:10.1137/0105003.
• ↑ Tomizawa, N. “On Some Techniques Useful for Solution of Transportation Network Problems.” Networks 1, no. 2 (1971): 173–94. doi:10.1002/net.3230010206.
• ↑ Bertsekas, Dimitri P. “Auction Algorithms for Network Flow Problems: a Tutorial Introduction.” Computational Optimization and Applications 1 (1992): 7–66.
• ↑ Zavlanos, Michael M, Leonid Spesivtsev, and George J Pappas. “A Distributed Auction Algorithm for the Assignment Problem,” Proceedings of IEEE CDC'08, 1212–17, IEEE, 2008. doi:10.1109/CDC.2008.4739098.
• ↑ Hopcroft, John E, and Richard M Karp. “An $N^{5/2} $ Algorithm for Maximum Matchings in Bipartite Graphs.” SIAM Journal on Computing 2, no. 4 (1973): 225–31. doi:10.1137/0202019.
• Problem level
• Articles in progress

Navigation menu

Personal tools.

• Create account
• View source
• View history
• Recent changes

File storage

• Upload file
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• This page was last edited on 6 March 2018, at 17:08.
• Content is available under Creative Commons Attribution unless otherwise noted.
• Privacy policy
• About Algowiki
• Disclaimers

Please enable JavaScript to pass antispam protection! Here are the instructions how to enable JavaScript in your web browser http://www.enable-javascript.com . Antispam by CleanTalk.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Computer Science Principles

Course: ap®︎/college computer science principles   >   unit 4, the building blocks of algorithms.

• Expressing an algorithm

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

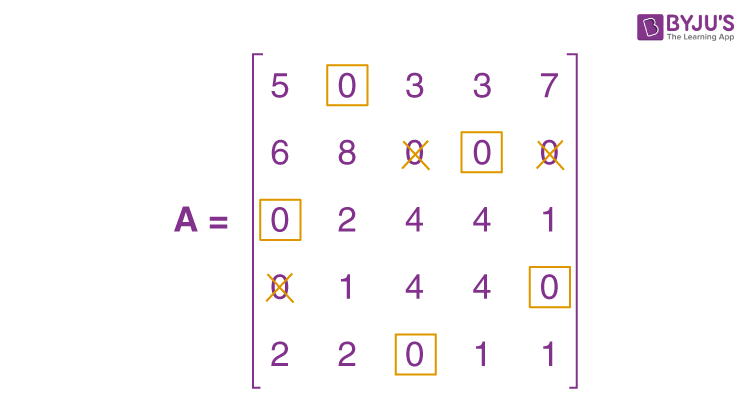
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

An anytime assignment algorithm: From local task swapping to global optimality

• Published: 03 July 2013
• Volume 35 , pages 271–286, ( 2013 )

Cite this article

• Lantao Liu 1 &
• Dylan A. Shell 1  

749 Accesses

16 Citations

Explore all metrics

The assignment problem arises in multi-robot task-allocation scenarios. Inspired by existing techniques that employ task exchanges between robots, this paper introduces an algorithm for solving the assignment problem that has several appealing features for online, distributed robotics applications. The method may start with any initial matching and incrementally improve the current solution to reach the global optimum, producing valid assignments at any intermediate point. It is an any-time algorithm with a performance profile that is attractive: quality improves linearly with stages (or time). Additionally, the algorithm is comparatively straightforward to implement and is efficient both theoretically (complexity of \(O(n^3\lg n)\) is better than many widely used solvers) and practically (comparable to the fastest implementation, for up to hundreds of robots/tasks). The algorithm generalizes “swap” primitives used by existing task exchange methods already used in the robotics community but, uniquely, is able to obtain global optimality via communication with only a subset of robots during each stage. We present a centralized version of the algorithm and two decentralized variants that trade between computational and communication complexity. The centralized version turns out to be a computational improvement and reinterpretation of the little-known method of Balinski–Gomory proposed half a century ago. Thus, deeper understanding of the relationship between approximate swap-based techniques—developed by roboticists—and combinatorial optimization techniques, e.g., the Hungarian and Auction algorithms—developed by operations researchers but used extensively by roboticists—is uncovered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Communication constrained task allocation with optimized local task swaps.

Trajectory Planning and Assignment in Multirobot Systems

Distributed assignment with limited communication for multi-robot multi-target tracking

The algorithm was first presented in the 2012 Robotics: Science and Systems conference (Liu and Shell 2012a ).

Every traversed entry on the path segments, no matter whether it is assigned or unassigned, must connect to a new entry in other rows, requiring a message be passed. The number is approximately half of all the traversed entries since each entry is counted twice for the analysis of communication complexity.

Akgül, M. (1992). The linear assignment problem. In M. Akgiil & S. Tufecki (Eds.), Combinatorial optimization (pp. 85–122). Berlin: Springer.

Chapter   Google Scholar  

Balinski, M. L., & Gomory, R. E. (1964). A primal method for the assignment and transportation problems. Management Science , 10 (3), 578–593.

Article   Google Scholar  

Berhault, M., Huang, H., Keskinocak, P., Koenig, S., Elmaghraby, W., Griffin, P., & Kleywegt, A. J. (2003). Robot Exploration with Combinatorial Auctions (pp. 1957–1962). In Proceedings of the IROS .

Bertsekas, D. P. (1990). The auction algorithm for assignment and other network flow problems: A tutorial. Interfaces , 20 (4), 133–149.

Burkard, R., Dell’Amico, M., & Martello, S. (2009). Assignment problems . New York, NY: Society for Industrial and Applied Mathematics.

Book   MATH   Google Scholar  

Cao, Y. U., Fukunaga, A. S., & Kahng, A. B. (1997). Cooperative mobile robotics: Antecedents and directions. Autonomous Robots , 4 , 226–234.

Chaimowicz, L., Campos, M. F. M., & Kumar, V. (2002). Dynamic role assignment for cooperative robots (pp. 293–298). In Proceedings of the IEEE International Conference on Robotics and Automation .

Cunningham, W., & Marsh, A. B, I. (1978). A primal algorithm for optimum matching. Mathematical Programming Study , 8 , 50–72.

Google Scholar  

Dantzig, G. (1963). Linear programming and extensions . Princeton: Princeton University Press.

MATH   Google Scholar  

Dias, M.B., & Stentz, A. (2002). Opportunistic optimization for market-based multirobot control (pp. 2714–2720 ). In Proceedings of the IROS .

Dias, M. B., Zlot, R., Kalra, N., & Stentz, A. (2006). Market-based multirobot coordination: A survey and analysis. In Proceedings of the IEEE .

Edmonds, J., & Karp, R. M. (1972). Theoretical improvements in algorithmic efficiency for network flow problems. Journal of the ACM , 19 (2), 248–264.

Article   MATH   Google Scholar  

Farinelli, A., Iocchi, L., Nardi, D., & Ziparo, V. A. (2006). Assignment of dynamically perceived tasks by token passing in multi-robot systems. In Proceedings of the IEEE, Special Issue on Multi-robot Systems .

Gerkey, B. P., & Matarić, M. J. (2004). A formal analysis and taxonomy of task allocation in multi-robot systems. International Journal of Robotics Research , 23 (9), 939–954.

Giordani, S., Lujak, M., & Martinelli, F. (2010). A distributed algorithm for the multi-robot task allocation problem. LNCS: Trends in Applied Intelligent Systems , 6096 , 721–730.

Goldberg, A. V., & Kennedy, R. (1995). An efficient cost scaling algorithm for the assignment problem. Mathematics Programs , 71 (2), 153–177.

Article   MathSciNet   MATH   Google Scholar  

Golfarelli, M., Maio, D., & Rizzi, S. (1997). Multi-agent path planning based on task-swap negotiation (pp. 69–82). In Proceedings of the UK Planning and Scheduling Special Interest Group, Workshop .

Koenig, S., Keskinocak, P., & Tovey, C. A. (2010). Progress on agent coordination with cooperative auctions. In Proceedings of the AAAI .

Kuhn, H. W. (1955). The Hungarian method for the assignment problem. Naval Research Logistic Quarterly , 2 , 83–97.

Lagoudakis, M. G., Markakis, E., Kempe, D., Keskinocak, P., Kleywegt, A., Koenig, S., et al. (2005). Auction-based multi-robot routing. In Robotics: Science and Systems . Cambridge: MIT Press.

Liu, L., & Shell, D. (2011). Assessing optimal assignment under uncertainty: An interval-based algorithm. International Journal of Robotics Research , 30 (7), 936–953.

Liu, L., & Shell, D. (2012a). A distributable and computation-flexible assignment algorithm: From local task swapping to global optimality. In Proceedings of Robotics: Science and Systems , Sydney, Australia.

Liu, L., & Shell, D. (2012b). Large-scale multi-robot task allocation via dynamic partitioning and distribution. Autonomous Robots , 33 (3), 291–307.

Nanjanath, M., & Gini, M. (2006). Dynamic task allocation for robots via auctions (pp. 2781–2786). In Proceedings of the ICRA .

Parker, L. E. (2008). Multiple mobile robot systems. In B. Siciliano & O. Khatib (Eds.), Handbook of robotics chapter 40 . Berlin: Springer.

Sandholm, T. (1998). Contract types for satisficing task allocation: I Theoretical results (pp. 68–75). In Proceedings of the AAAI Spring Symposium: Satisficing Models .

Sariel, S., & Balch, T. (2006). A distributed multi-robot cooperation framework for real time task achievement. In Proceedings of Distributed Autonomous Robotic Systems .

Stone, P., Kaminka, G. A., Kraus, S., & Rosenschein, J. S. (2010). Ad Hoc autonomous agent teams: Collaboration without pre-coordination. In Proceedings of the AAAI .

Thomas, L., Rachid, A., & Simon, L. (2004). A distributed tasks allocation scheme in multi-UAV context (pp. 3622–3627). In Proceedings of the ICRA .

Wawerla, J., & Vaughan, R. T. (2009). Robot task switching under diminishing returns (pp. 5033–5038). In Proceedings of the 2009 IEEE/RSJ international conference on Intelligent robots and systems, IROS’09 .

Zavlanos, M. M., Spesivtsev, L., & Pappas, G. J. (2008). A distributed auction algorithm for the assignment problem. In Proceedings of the CDC .

Zheng, X., & Koenig, S. (2009). K-swaps: cooperative negotiation for solving task-allocation problems (pp. 373–378). In Proceedings of the International Joint Conferences on Artificial Intelligence (IJCAI) .

Zilberstein, S. (1996). Using anytime algorithms in intelligent systems. AI Magazine , 17 (3), 73–83.

Download references

Author information

Authors and affiliations.

Department of Computer Science and Engineering, Texas A&M University, College Station, TX, USA

Lantao Liu & Dylan A. Shell

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Lantao Liu .

Rights and permissions

Reprints and permissions

About this article

Liu, L., Shell, D.A. An anytime assignment algorithm: From local task swapping to global optimality. Auton Robot 35 , 271–286 (2013). https://doi.org/10.1007/s10514-013-9351-2

Download citation

Received : 02 October 2012

Accepted : 20 June 2013

Published : 03 July 2013

Issue Date : November 2013

DOI : https://doi.org/10.1007/s10514-013-9351-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Multi-robot task allocation
• Decentralized assignment
• Anytime algorithms
• Task swapping
• Find a journal
• Publish with us
• Track your research

FIT 100 Assignment 3

Algorithms:   Writing the perfect instructions [1]

Introduction

Before we proceed to programming computers, we need to prepare ourselves by learning how to think about programming.   At the heart of programming is the algorithm , basically a very carefully expressed problem-solving strategy , usually in the form of a structured set of instructions.   We say we “use” or “apply” an algorithm to solve the problem it was designed for.   In everyday life, when we think of instructions, we mean instructions for other people to follow, rather than a machine, and we can conveniently make many unstated assumptions and get away with being ambiguous.   Unlike instructions for people, instructions for computers can leave no room for misinterpretation, so algorithms require an extreme level of precision that will take some getting used to.   Following the guidelines discussed in Chapter 10, in this assignment, we will exercise our algorithmic thinking on a wide variety of problems, ranging from everyday tasks to mathematical problems.

·     concepts

1.       algorithm

2.       input, output

3.       degree of precision required in an algorithm

4.       control flow

5.       conditional

6.       iteration

·     skills

1.       writing an algorithm, given a properly specified problem statement

2.       identifying examples of conditionals and iteration in algorithms

·     Chapter 10:   Algorithmic Thinking

Required Resources

No computers are required.   This assignment consists entirely of written exercises.

All key vocabulary terms used in this assignment are listed below, with closely related words listed together:

algorithm , program control flow conditional, condition iteration, looping, loop condition

Discussion and Procedure

You will be writing algorithms for one kind of problem in this assignment.   However, there are more points possible for tackling an algorithm listed in Part 2 or 3.   No matter which problem you choose for writing an algorithm, remember to answer the 2 questions at the end of the assignment as well.

In Part 1 there are algorithm for completing an everyday task like doing laundry or making a sandwich.   In Part 2, there are options to write algorithms for special everyday tasks carefully chosen to have strong similarities to mathematical or computing problems.   For example, locating a word’s definition in a dictionary is an example of a “search problem,” using computer science terminology.   (Chapter 10’s CD rack sorting example also falls into this category.)   Finally, in Part 3 there are problems that are explicitly mathematical or computational in nature (e.g., finding the average of a large set of numbers).   You are instructed to choose one problem from one of these three groups and write an algorithm.   For whatever single algorithm you write, make sure to follow the following instructions:

Instructions for Writing Algorithms

For each problem stated, write a carefully worded and structured set of instructions for solving the problem.   Just as in the example algorithm in Chapter 10 (for sorting a CD rack), include the following sections, described in detail:

·     inputs or start state, including a list of required materials, if applicable (This might seem obvious for physical tasks like preparing a sandwich.   However, even for mathematical problems, you might want to note which quantities you want to keep track of.)

·     outputs or end result(s)

·     numbered steps

Always keep conscious of the assumptions you are making by writing them down explicitly.   You should adhere to the guidelines discussed in Chapter 10 and follow the format shown in the sample solution below.   (See the CD rack sorting example in Chapter 10 for a more extended example.)

Remember, there is no one right answer .   Many different algorithms might be acceptable for each problem.   Due to the flexibility of the English language, the same algorithm can often be expressed in more than one way.   In addition, there is almost always more than one way to solve a problem.   They might differ in their complexity, time required, and other aspects, which are important differences to consider, but they can all be valid algorithms for the problem.

Finally, both as you write and after you are finished, check your algorithm to make sure it satisfies all of the properties discussed at the beginning of Chapter 10. We have summarized them here in the form of questions you can ask yourself to check your algorithm:

1.              Inputs specified.   Do you precisely describe all of the data (or materials) needed for the algorithm?

2.              Outputs specified.   Do you precisely describe the results of your algorithm?   Your outputs description should clearly state what the algorithm is supposed to do and solve the problem the algorithm is designed for.

3.              Definiteness.   As discussed earlier, an algorithm must be expressed very precisely.   An ambiguous algorithm, if misinterpreted, might be ineffective at solving the problem it was designed for.   It is easy to get carried away, however, and include details that are not essential to the algorithm’s correctness.    Ask yourself the following as you write:   Is this detail essential to the algorithm’s correctness?   Does it add important information that is not evident from what you have already written?   Include the detail if you answer, “yes,” to these questions.

4.              Effectiveness.   Are the required resources (whether they be information or the ability to do certain things) realistic and reasonable?   For instance, an algorithm for converting a temperature from degrees Fahrenheit to Celsius that relies on looking up the temperature in a Fahrenheit-Celsius conversion table is hardly interesting or useful.

5.              Finiteness.   Are you sure that the algorithm actually finishes?   For instance, one algorithm for finding a specific playing card in a deck is to repeat the following:   Shuffle the deck and check the top card.   Strictly speaking, the card you are looking for might never end up at the top of the deck, no matter how many times you reshuffle.   (That would be pretty rotten luck, but it is possible.)   In contrast, checking the whole deck, one card at a time, while time-consuming, is an algorithm that is guaranteed to finish.   At worst, your card would end up being the last one you check.

Before we begin, we will go through a simple example.   Notice that each problem statement in this assignment is very carefully stated, with as many details and as few implicit assumptions as possible.   This is no accident.   It is only reasonable that a detailed and precise algorithm requires an equally carefully stated problem.

Example problem :   Given a VCR, TV, and videotape of twelve episodes of your favorite television show, each 30 minutes long, find a specified episode and cue the tape to the start of the episode.   For instance, suppose you have already seen all but one of the episodes, but you are not sure where the one episode is on the tape.   Your objective is to find this episode on the tape.   Assume that the TV and VCR are both on, and that the tape is in the VCR, cued to an unknown location (i.e., not necessarily rewound).

Example algorithm .  

START STATE :   videotape of twelve 30 min. episodes, VCR, TV with assumptions as stated in problem above; ability to recognize one specific episode

END RESULT:   videotape cued to beginning of specified episode

ASSUMPTIONS:  

o         VCR has tape counter that shows tape position in hours and minutes.

o         Episodes begin at 30 min. multiples, i.e., the first episode is at time 0:00, the second at 0:30, the third at 1:00 , etc.   There is no other video recorded on the tape between episodes.

1)      Rewind tape to start.

2)      Reset tape counter.

3)      Play tape for a few minutes to check whether the episode is the one you are looking for.   If so, proceed to Step 5; otherwise, proceed to Step 4.

4)      Stop play, and fast forward the tape.   Watch the counter for the next 30 min. multiple, and press stop when the tape reaches that point, which should be the start of the next episode on the tape.   For example, if you stopped the tape at 2:04 (two hours, four minutes), fast forward until the counter reads 2:30 .   Go to Step 3.

5)      Stop play, and rewind to the previous 30 min. multiple using the tape counter.   For example, if you recognize the episode you are looking for and the counter reads 3:32 (three hours, 32 minutes), rewind to 3:30 .

Part 1.       Algorithms for Everyday Problems   [worth 8 points- the assignment minimum]

important advice :   Do not assume that problems in this part will be easy just because the procedures for these tasks might be second nature to you.   In fact, the more familiar you are with a task, the more likely it is that you will make implicit assumptions and skip details in your algorithm.

Choose ONE of the problems below and write an algorithm to solve it.   Assume a reasonably equipped kitchen as the context.

1a-1.   Prepare a bowl of cold cereal.   You may choose to include fruit or other ingredients beyond cereal and milk, but make sure to state them explicitly.   Assume that a carton of milk is in the refrigerator.

1a-2.   Prepare a sandwich.   Make sure to state what kind of sandwich you are making and what ingredients and utensils are required.   Again, assume all required ingredients are in the kitchen, refrigerated if needed.

1a-3.   Prepare a cup of tea using a tea bag.   You may describe adding cream, sugar, lemon, honey, etc., but mention these ingredients in your write-up.

Each of the following everyday problems involves repeating some steps in the procedure (just as Step 4 in the above example can be repeated).  

1b-1.   Given a pile of pens, find and discard the ones that do not write any more.

1b-2.   Suppose you are told that your favorite movie is on television right now, but you are not sure which channel it is on.   Without the use of a program guide (that is, without using things like TV Guide or the newspaper program listings), find the channel broadcasting the movie.   Assume, of course, that you could recognize any part of the movie if you saw it.

1b-3.   Brush your teeth.

1b-4.   Wash and dry a load of laundry using coin operated washing machine and dryer.

Part 2.       Algorithms for Computational Everyday Problems [worth up to 12 points]

The problems in this section are real-life versions of computational problems.  

2-1.       Given two words, determine which would come first in alphabetical order.   Do not use a dictionary or other reference book.

2-2.       Given a bag full of cherries, determine whether you could split them evenly among seven people (so that each person has the same number of cherries and none are left over).   The result is a yes or no answer.

2-3.       Given a restaurant check subtotal (before tax) and total (after tax), calculate how much you should leave for a 15% tip.

2-4.       Given fifty apples and a two-pan balance (which can determine whether two items have the same weight), determine which two (if any) have the same weight (have weight close enough that the balance measures them as being equal).

Part 3.       Algorithms for Computational Problems [worth up to 15 points]

Problems in this section are obviously computational, involving computing mathematically interesting results.   They are fundamentally different from the problems in the previous two parts of the assignment in that they involve no physical process.   That is, these problems involve manipulating numbers rather than physical objects like foods, pens, or laundry detergent.  

3-1.       Given a set of 20 numbers, compute the average of the numbers.

3-2.       Given a set of 100 numbers, find the largest and smallest numbers in the set.

Part 4.       Recognizing Control Flow Patterns

Some algorithms are very simple, and applying them just involves proceeding from one step to the next (sequential execution).   We have already seen examples of algorithms, however, which involve skipping ahead to a later step or repeating an earlier step, depending on certain conditions.   Control flow is the programming term used to describe the order in which the steps are executed, and we will discuss two common ways control flow diverges from simple, sequential execution.   In the Post-Assignment Questions, you are asked to examine the algorithms you wrote and identify at least one example of each of these control flow patterns.

Conditionals:   The keyword is “if.”   A conditional (also known as a branch ) is when control flow reaches a point where it can proceed to one of two (or more) alternatives.   The condition is what determines which step to proceed to.   For example, to round off a number to its nearest integer, you first need to check the following condition:   whether the fractional part is less than 0.5.   If so, the result is just the integer part; otherwise, you add one to the integer part.   Use of the phrase structure “if…then…” and instructions to skip ahead/back to other steps in an algorithm are hallmarks of the conditional.

Iteration:   Controlled repetition.   Iteration is basically the repetition of one or more steps in an algorithm.   Iteration is related to the conditional in that the number of times you do the repetition is usually controlled by a condition.   Iteration is also called looping and the condition is accordingly called the loop condition .   The video searching example algorithm at the start of this assignment has a loop in Steps 3-4, where the conditional in Step 3 (checking whether the episode is the one you are looking for) determines whether you repeat Step 4’s fast-forwarding.

Understanding the concepts of control flow and the two standard patterns of the conditional and iteration will help you a great deal as you proceed to expressing algorithms in a programming language.

Post-Assignment Questions

Write your answers after completing the main part of the assignment:

1.       Identify one example of iteration in the algorithm you wrote for this assignment.   Explain which steps are being repeated and what determines when the repetition stops.   It is possible that you did not use iteration for your algorithm: if that is the case, then say so-but be VERY SURE that it is the case!

2.       Identify at least one example of a conditional in the algorithm you wrote for this assignment. It is possible that you did not use iteration for your algorithm: if that is the case, then say so-but be VERY SURE that it is the case!

[1] Algorithms exercise written by Ken Yasuhara .   Edited by Grace Beauchane Whiteaker