lines of symmetry year 4 reasoning and problem solving

Planning tool

Year levels.

• {{PlanningToolMenuItem.Name}}

Expected level of development

Australian Curriculum Mathematics V9 : AC9M4SP03

Numeracy Progression : Understanding geometric properties: P4

At this level, students investigate reflection symmetry and develop their understanding of how the line of symmetry defines the two aspects of a ‘mirror’ image of the figure into two congruent halves. They explore rotational symmetry using familiar 2D shapes, letters or numbers.

Make explicit through relevant examples, modelling and investigation that a figure can have one line of symmetry, several lines of symmetry, or no lines of symmetry.

Teaching and learning summary:

• Model how to work out if a figure has a line of symmetry.
• Use practical activities to explore symmetry.
• Look for examples of symmetry in nature and other real world objects.

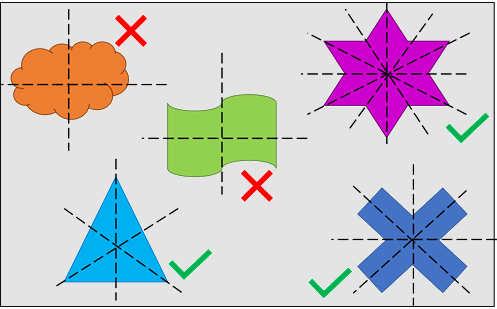
• draw missing portions of a symmetrical figure
• describe the line and rotational symmetry by manually cutting, folding and turning shapes and by using digital technologies
• explain why some figures have no line of symmetry.

Some students may:

• have trouble visualising the line of symmetry and mistakenly draw a line of reflection along an incorrect axis. Use practical examples where students fold simple shapes to check their predictions.
• identify one line of symmetry and not understand a shape may have more than one line of symmetry. Use a task which challenges students to find as many lines of symmetry as possible or provide shapes that have multiple lines of symmetry and make explicit the lines of symmetry.
• believe that, like a square, a rectangle has 4 lines of symmetry when it only has two. Use practical examples where students fold a rectangle to check their predictions.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

• We are learning about symmetrical shapes.

Why are we learning about this?

• Symmetry is all around us. You can find examples in nature, art, building and design.
• Can you draw the half that is missing?
• How do you know what to draw?
• Explain your answer.

• Would this activity work for all objects? Why or why not?

Success criteria

• complete the remaining half of an object that is symmetrical
• describe what symmetry is and what it isn’t with some examples.
• We are learning how to define symmetry.
• We are learning how to draw shapes or objects with their lines of symmetry.
• We are using symmetry to recognise and form patterns.

What I want you to do

• Which one is symmetrical?
• Which one has no line of symmetry?

• Write each one in capital letters.
• Estimate how many of the letters are symmetrical.
• Check to see if each letter has a vertical line of symmetry or a horizontal line of symmetry or both.
• Draw your results to show how you worked out which letters are symmetrical. How did your estimate compare?
• recognise when a letter has no lines of symmetry
• identify the lines of symmetry.

Please note:  This site contains links to websites not controlled by the Australian Government or ESA. More information  here .

Go to section

Teaching strategies.

A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well. 

Mathematics investigation

By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.

Explicit teaching

Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.

Culturally responsive pedagogies

Culturally responsive pedagogy is a form of teaching that incorporates learners’ cultural background and histories into classroom practice.

Teaching resources

A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.

Symmetry hunt

Explore line and rotational symmetry using suggested learning tasks.

Line of symmetry

Students identify and draw the lines of symmetry by folding 2D shapes.

Fold and cut

In this unit, students explore line or reflective symmetry. Students develop an understanding of what line symmetry is and the names and attributes of common 2D mathematical shapes.

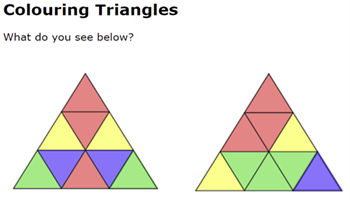
Colouring triangles

Students explore ways of colouring a set of triangles so that they make symmetrical patterns.

reSolve: Authentic problems – expanded square

This sequence of four lessons explores concepts around informal area and symmetry.

reSolve: Transformations – frieze patterns

This sequence of three lessons explores transformation and symmetry by engaging students in the design of friezes.

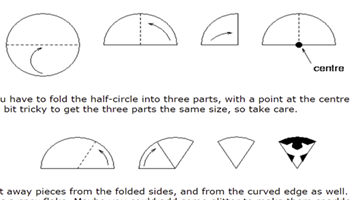
Making maths: snowflakes

This task shows students how to fold and cut paper to make a model snowflake, demonstrating six lines of symmetry.

Getting in line

A useful starting point to explore line symmetry in 2D shapes.

Pattern matching

In this unit, students explore lines of symmetry in pictures, shapes and patterns and use their own words to describe the symmetry.

Sea symmetry

Use a mirror to explore line (reflection) symmetry to complete a drawing.

Grid symmetry

Use a problem-solving approach to investigate reflection symmetry.

Finding lines of symmetry

Students explore line symmetry by drawing lines of symmetry to divide shapes into two halves.

Geometric pictures of one half

Students draw on geometric reasoning, symmetry and understanding of a half to compare the area of a square.

Fold and cut 2

This unit involves folding and cutting paper to produce and perceive number patterns and geometric shapes.

Relevant assessment tasks and advice related to this topic.

By the end of Year 4, students are identifying line and rotational symmetry in plane shapes and creating symmetrical patterns.

Mathematics Year 4 Geometry: Symmetry – ACARA

The Year 4 Mathematics achievement standard. For the parts of the achievement standard targeted in the assessment, refer to Sample 6.

Lines of Symmetry

Maths Lesson Description

Classroom Stars

Year 4 | Lines of Symmetry Worksheets

In these Year 4 lines of symmetry worksheets , pupils are prompted to draw the lines of symmetry for six different 2D shapes. Following this, they are presented with a group of shapes and tasked with writing the number of lines of symmetry each shape possesses.

This Year 4 lines of symmetry worksheet engages learners in observing and identifying where lines of symmetry can be formed. It encourages them to draw these lines, enhancing their understanding of symmetry concepts. Engaging with lines of symmetry worksheets strengthens children’s geometry skills as they explore the properties of 2D shapes.

Our Year 4 lines of symmetry worksheets are aligned with KS2 geometry: properties of shapes on the primary national curriculum. All of our Year 4 geometry: properties of shapes worksheets can be used with your ideas for primary maths activities, learning resources, teaching material, visual aids, games, differentiation, display boards, homework, and lesson plans.

You may like our Year 4 Drawing Angles in Shapes Worksheets .

Explore all of our Year 4 maths worksheets .

Access this resource and thousands more for just £9.95 per year

You might also like...

Questions for Arguments Flashcards

Year 3 | Counting in 50s Worksheets

Year 4 | Place Value: 4-Digit Numbers Worksheets

You have subscribed to our newsletter.

You have joined the list to receive our newsletter! Be sure to look out for all our latest resources, news and reads from our blog.

Access this AI tool and lots more for just £9.95 per year

Email address updated

Your email address has been updated. A confirmation has been sent to your previous email address.

Check your email

We have sent you an email with a link to create a new password.

Remember to check the junk folder in case the link was sent there.

Your message has been received

Thank you for getting in contact with us! A member of our team will do their best to get back to you as soon as possible.

Request for school membership received

Thank you for providing us with your details. A member of our team will get back to you as soon as possible with the next steps.

New password created

Your new password has been created. A confirmation email has been sent to you.

Download your free resource pack

Thank you for joining the list to receive our newsletter! Click below to download your free sample resource pack.

Username or Email

Remember Me

Lost Password?

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Symmetry Challenge

• Getting Started
• Student Solutions
• Teachers' Resources

Symmetry Challenge printable sheet

In this activity, we are going to shade the squares of this grid with one colour to make different designs.

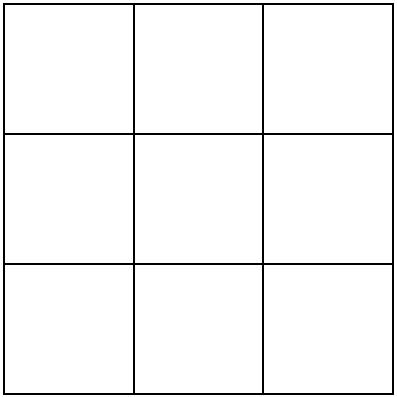
There are a few rules that our designs need to follow:

• Whole squares have to be shaded, rather than parts of squares.
• Each design must have at least one line of symmetry.
• Each new design you come up with must be different from all of the others. If two designs would look the same if you rotated or reflected them, they do not count as different designs in this task.

Have a go at making some designs. How many can you find? You might like to shade your designs on squared paper or on  this sheet of blank grids .

If you wanted to find every possible design, how would you do this?

• International
• Education Jobs
• Schools directory
• Resources Education Jobs Schools directory News Search

Symmetry Mastery Challenge Yr 4

Subject: Mathematics

Age range: 7-11

Resource type: Worksheet/Activity

Last updated

22 February 2018

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Creative Commons "Attribution"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

Thank you for sharing. Super sheet to get the children to think.<br />

Empty reply does not make any sense for the end user

slingysquirrelstitch

This was just the thing I needed! I also asked the children to draw in the line of symmetry. Thanks for sharing

This is just what I was looking for thank you for sharing and saving me time.

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• £ 0.00 0 items

Year 4 Lines of Symmetry Maths Challenge

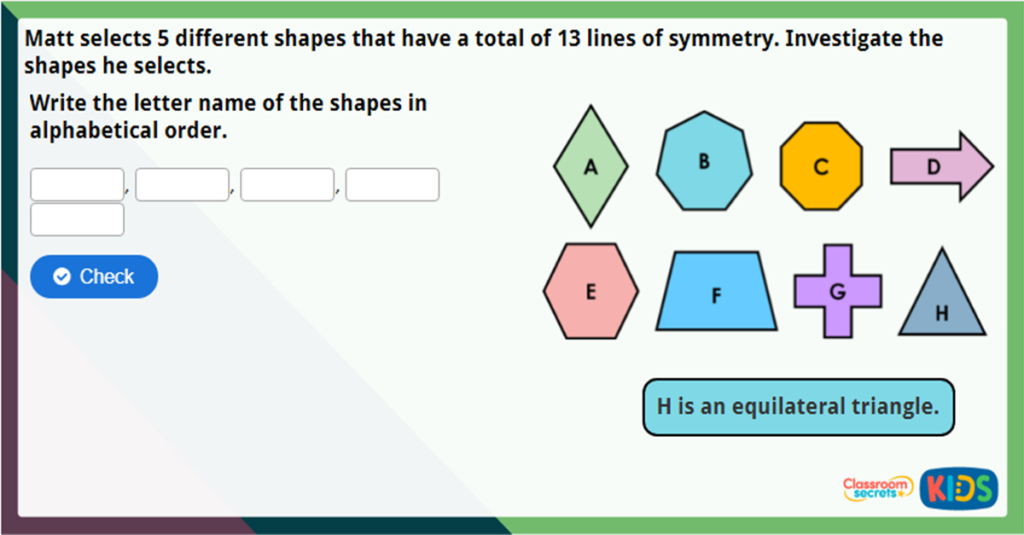
This Year 4 Lines of Symmetry Challenge checks children’s understanding of finding lines of symmetry. Children will help Matt to select the correct shapes to find a given number of lines of symmetry.

If you would like to access  additional resources which link to this maths challenge, you can purchase a subscription for only £5.31 per month on our sister site, Classroom Secrets .

Teacher Specific Information

This Year 4 Lines of Symmetry Challenge checks pupils’ understanding of finding lines of symmetry. Pupils will help Matt to select the correct shapes to find a given number of lines of symmetry.

National Curriculum Objectives

Properties of Shapes

Mathematics Year 4: (4G2b) Identify lines of symmetry in 2-D shapes presented in different orientations

Have you visited our sister site yet?

Primary resources for teachers

Classroom Secrets provides high-quality, affordable teaching resources that children love, and teachers trust.

Stay in touch

01422 419608

[email protected]

Interested in getting weekly updates from us? Then sign up to our newsletter here!

Information

• Cookie Policy
• Privacy Settings
• Terms and Conditions
• End User License Agreement

Copyright: Classroom Secrets 2024

Company number: 8401067

VAT number: 248824574

Designed by Classroom Secrets

Bootstrap Modal Title

Bootstrap modal body text should be here.