homework 2 2 solving inequalities

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

We call that "solved".

Example: x + 2 > 12

Subtract 2 from both sides:

x + 2 − 2 > 12 − 2

x > 10

How to Solve

Solving inequalities is very like solving equations , we do most of the same things ...

... but we must also pay attention to the direction of the inequality .

Some things can change the direction !

< becomes >

> becomes <

≤ becomes ≥

≥ becomes ≤

Safe Things To Do

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

But these things do change the direction of the inequality ("<" becomes ">" for example):

• Multiply (or divide) both sides by a negative number
• Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality :

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra ), like this:

Example: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 − 3 < 7 − 3    

And that is our solution: x < 4

In other words, x can be any value less than 4.

What did we do?

And that works well for adding and subtracting , because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5

If we subtract 5 from both sides, we get:

12 − 5 < x + 5 − 5    

That is a solution!

But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

Do you see how the inequality sign still "points at" the smaller value (7) ?

And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying ).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number :

Example: 3y < 15

If we divide both sides by 3 we get:

3y /3 < 15 /3

And that is our solution: y < 5

Negative Values

Well, just look at the number line!

For example, from 3 to 7 is an increase , but from −3 to −7 is a decrease.

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Example: −2y < −8

Let us divide both sides by −2 ... and reverse the inequality !

−2y < −8

−2y /−2 > −8 /−2

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Example: bx < 3b

It seems easy just to divide both sides by b , which gives us:

... but wait ... if b is negative we need to reverse the inequality like this:

But we don't know if b is positive or negative, so we can't answer this one !

To help you understand, imagine replacing b with 1 or −1 in the example of bx < 3b :

• if b is 1 , then the answer is x < 3
• but if b is −1 , then we are solving −x < −3 , and the answer is x > 3

The answer could be x < 3 or x > 3 and we can't choose because we don't know b .

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Example: x−3 2 < −5.

First, let us clear out the "/2" by multiplying both sides by 2.

Because we are multiplying by a positive number, the inequalities will not change.

x−3 2 ×2 < −5  ×2  

x−3 < −10

Now add 3 to both sides:

x−3 + 3 < −10 + 3    

And that is our solution: x < −7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 2x^2-x\gt 0
• (x+3)^2\le 10x+6
• \left|3+2x\right|\le 7
• \frac{\left|3x+2\right|}{\left|x-1\right|}>2
• What are the 4 inequalities?
• There are four types of inequalities: greater than, less than, greater than or equal to, and less than or equal to.
• What is a inequality in math?
• In math, inequality represents the relative size or order of two values.
• How do you solve inequalities?
• To solve inequalities, isolate the variable on one side of the inequality, If you multiply or divide both sides by a negative number, flip the direction of the inequality.
• What are the 2 rules of inequalities?
• The two rules of inequalities are: If the same quantity is added to or subtracted from both sides of an inequality, the inequality remains true. If both sides of an inequality are multiplied or divided by the same positive quantity, the inequality remains true. If we multiply or divide both sides of an inequality by the same negative number, we must flip the direction of the inequality to maintain its truth.

inequalities-calculator

• High School Math Solutions – Inequalities Calculator, Linear Inequalities Solving linear inequalities is pretty simple. A linear inequality is an inequality which involves a linear function....
• Solve Inequalities Learning Outcomes Describe solutions to inequalities Represent inequalities on a number line Represent inequalities using interval notation Solve single-step inequalities Use the addition and multiplication properties to solve algebraic inequalities and express their solutions graphically and with...
• 3A.2 Solve Compound Inequalities 3A.2 Learning Objectives Use interval notation to describe intersections and unions Use graphs to describe intersections and unions Solve compound inequalities in the form of or and express the solution graphically and with an interval Express solutions to inequalities graphically and with interval...
• Linear Inequalities and Systems of Linear Inequalities in Two Variables Learning Objectives Define solutions to a linear inequality in two variables Identify and follow steps for graphing a linear inequality in two variables Identify whether an ordered pair is in the solution set of a linear inequality Define solutions to systems of linear inequalities Graph a system o...
• Compound Inequalities Learning Objectives Describe sets as intersections or unions Use interval notation to describe intersections and unions Use graphs to describe intersections and unions Solve compound inequalities—OR Solve compound inequalities in the form of or and express the solution graphically and with an inter...
• Inequalities Introduction to Inequalities Inequalities are used to demonstrate relationships between numbers or expressions. Learning Objectives Explain what inequalities represent and how they are used Key Takeaways Key Points An inequality describes a relationship between two different values. The notation me...
• Systems of Linear Inequalities 6.3 Learning Objectives Define solutions to systems of linear inequalities Graph a system of linear inequalities and define the solutions region Verify whether a point is a solution to a system of inequalities Identify when a system of inequalities has no solution Solutions from graphs of linear in...
• 3A.1 Single- and Multi-Step Inequalities 3A.1 Learning Objectives Represent inequalities on a number line Represent inequalities using interval notation Use the addition and multiplication properties to solve algebraic inequalities Express solutions to inequalities graphically, with interval notation, and as an inequality Sometimes there...
• Reading: Solving One-Step Inequalities Inequalities are similar to equations in that they show a relationship between two expressions. We solve and graph inequalities in a similar way to equations. However, there are some differences that we will talk about in this chapter. The main difference is that for linear inequalities the answer i...
• Linear Inequalities and Absolute Value Inequalities It is not easy to make the honor role at most top universities. Suppose students were required to carry a course load of at least 12 credit hours and maintain a grade point average of 3.5 or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore...
• Poverty and Economic Inequality Figure 1. Occupying Wall StreetOn September 17, 2011, Occupy Wall Street began in New York City’s Wall Street financial district. (Credit: modification of work by David Shankbone/Flickr Creative Commons) Occupy Wall Street In September 2011, a group of protesters gathered in Zuccotti Park in New Yo...

Please add a message.

Message received. Thanks for the feedback.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Algebra II : Solving Inequalities

Study concepts, example questions & explanations for algebra ii, all algebra ii resources, example questions, example question #1 : solving inequalities.

Add 4 to both sides.

Divide both sides by –7. When dividing by a negative value, we must also change the direction of the inequality sign.

Solve this inequality.

Split the inequality into two possible cases as follows, based on the absolute values.

Let's find the inequality of the first case.

Multiply both sides by x + 6.

Subtract x from both sides, then subtract 3 from both sides.

Divide both sides by 3.

Let's find the inequality of the second case.

Add x to both sides, then subtract 3 from both sides.

Divide both sides by 5.

Example Question #1 : Graphing Inequalities

Solve the compound inequality and express answer in interval notation:

Find the solution set of the inequality:

Sam's age is three years more than twice his brother's age. If the sum of their ages is at least 18, then was is the maximum possible age of Sam's brother?

In the problem, we are told that the sum of their ages is at least 18. Represent this with an inequality:

Sam's age is three years more than twice his brothers age. Write this mathematically as:

Example Question #4 : Solving Inequalities

Solve the inequality:

Example Question #5 : Solving Inequalities

Most of solving inequalities is straightforward algebra and we can manipulate them in the same way as equations in most cases. 

However, we must remember that when multiplying or dividing by negative numbers in inequalities, we have to switch the direction of the inequality. So we do the final division step and get the answer:

Example Question #6 : Solving Inequalities

In order to solve this inequality, we must first consolidate all of our values on one side.

This results in:

This gives us

Example Question #7 : Solving Inequalities

The two equations should be solved separately to get,

Example Question #1 : Writing Inequalities

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 10: One-step and two-step equations & inequalities

Combining like terms.

• Intro to combining like terms (Opens a modal)
• Combining like terms with negative coefficients & distribution (Opens a modal)
• Combining like terms with negative coefficients (Opens a modal)
• Combining like terms with rational coefficients (Opens a modal)
• Combining like terms with negative coefficients Get 5 of 7 questions to level up!
• Combining like terms with negative coefficients & distribution Get 3 of 4 questions to level up!
• Combining like terms with rational coefficients Get 3 of 4 questions to level up!

The distributive property & equivalent expressions

• The distributive property with variables (Opens a modal)
• Factoring with the distributive property (Opens a modal)
• Equivalent expressions: negative numbers & distribution (Opens a modal)
• Distributive property with variables (negative numbers) Get 3 of 4 questions to level up!
• Equivalent expressions: negative numbers & distribution Get 5 of 7 questions to level up!

Interpreting linear expressions

• Interpreting linear expressions: diamonds (Opens a modal)
• Interpreting linear expressions: flowers (Opens a modal)
• Writing expressions word problems (Opens a modal)
• Interpreting linear expressions Get 3 of 4 questions to level up!
• Writing expressions word problems Get 5 of 7 questions to level up!

Two-step equations intro

• Same thing to both sides of equations (Opens a modal)
• Intro to two-step equations (Opens a modal)
• Two-step equations intuition (Opens a modal)
• Worked example: two-step equations (Opens a modal)
• Two-step equations Get 5 of 7 questions to level up!

Two-step equations with decimals and fractions

• Two-step equations with decimals and fractions (Opens a modal)
• Find the mistake: two-step equations (Opens a modal)
• Two-step equations review (Opens a modal)
• Two-step equations with decimals and fractions Get 5 of 7 questions to level up!
• Find the mistake: two-step equations Get 3 of 4 questions to level up!

Two-step equation word problems

• Equation word problem: super yoga (1 of 2) (Opens a modal)
• Equation word problem: super yoga (2 of 2) (Opens a modal)
• Two-step equation word problem: computers (Opens a modal)
• Two-step equation word problem: garden (Opens a modal)
• Two-step equation word problem: oranges (Opens a modal)
• Interpret two-step equation word problems Get 3 of 4 questions to level up!
• Two-step equations word problems Get 3 of 4 questions to level up!

One-step inequalities

• Testing solutions to inequalities (Opens a modal)
• One-step inequalities examples (Opens a modal)
• One-step inequalities: -5c ≤ 15 (Opens a modal)
• One-step inequality word problem (Opens a modal)
• One-step inequalities review (Opens a modal)
• Testing solutions to inequalities Get 3 of 4 questions to level up!
• One-step inequalities Get 5 of 7 questions to level up!

Two-step inequalities

• Two-step inequalities (Opens a modal)
• Two-step inequality word problem: apples (Opens a modal)
• Two-step inequality word problem: R&B (Opens a modal)
• Two-step inequalities Get 5 of 7 questions to level up!
• Two-step inequality word problems Get 3 of 4 questions to level up!

2.5 Solve Linear Inequalities

Learning objectives.

By the end of this section, you will be able to:

• Graph inequalities on the number line
• Solve linear inequalities
• Translate words to an inequality and solve
• Solve applications with linear inequalities

Be Prepared 2.13

Before you get started, take this readiness quiz.

Translate from algebra to English: 15 > x . 15 > x . If you missed this problem, review Example 1.3 .

Be Prepared 2.14

Translate to an algebraic expression: 15 is less than x . If you missed this problem, review Example 1.8 .

Graph Inequalities on the Number Line

What number would make the inequality x > 3 x > 3 true? Are you thinking, “ x could be four”? That’s correct, but x could be 6, too, or 37, or even 3.001. Any number greater than three is a solution to the inequality x > 3 . x > 3 .

We show all the solutions to the inequality x > 3 x > 3 on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.

We can also represent inequalities using interval notation . There is no upper end to the solution to this inequality. In interval notation, we express x > 3 x > 3 as ( 3 , ∞ ) . ( 3 , ∞ ) . The symbol ∞ ∞ is read as “ infinity .” It is not an actual number.

Figure 2.2 shows both the number line and the interval notation.

We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, shows that the endpoint is included.

The inequality x ≤ 1 x ≤ 1 means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at x = 1 . x = 1 . We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions. See Figure 2.3 .

There is no lower end to those numbers. We write x ≤ 1 x ≤ 1 in interval notation as ( − ∞ , 1 ] . ( − ∞ , 1 ] . The symbol − ∞ − ∞ is read as “negative infinity.” Figure 2.3 shows both the number line and interval notation.

Inequalities, Number Lines, and Interval Notation

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals.

Example 2.48

Graph each inequality on the number line and write in interval notation.

ⓐ x ≥ −3 x ≥ −3 ⓑ x < 2.5 x < 2.5 ⓒ x ≤ − 3 5 x ≤ − 3 5

Try It 2.95

Graph each inequality on the number line and write in interval notation: ⓐ x > 2 x > 2 ⓑ x ≤ −1.5 x ≤ −1.5 ⓒ x ≥ 3 4 . x ≥ 3 4 .

Try It 2.96

Graph each inequality on the number line and write in interval notation: ⓐ x ≤ −4 x ≤ −4 ⓑ x ≥ 0.5 x ≥ 0.5 ⓒ x < − 2 3 . x < − 2 3 .

What numbers are greater than two but less than five? Are you thinking say, 2.5 , 3 , 3 2 3 , 4 , 4.99 2.5 , 3 , 3 2 3 , 4 , 4.99 ? We can represent all the numbers between two and five with the inequality 2 < x < 5 . 2 < x < 5 . We can show 2 < x < 5 2 < x < 5 on the number line by shading all the numbers between two and five. Again, we use the parentheses to show the numbers two and five are not included. See Figure 2.4 .

Example 2.49

ⓐ −3 < x < 4 −3 < x < 4 ⓑ −6 ≤ x < −1 −6 ≤ x < −1 ⓒ 0 ≤ x ≤ 2.5 0 ≤ x ≤ 2.5

Try It 2.97

Graph each inequality on the number line and write in interval notation:

ⓐ −2 < x < 1 −2 < x < 1 ⓑ −5 ≤ x < −4 −5 ≤ x < −4 ⓒ 1 ≤ x ≤ 4.25 1 ≤ x ≤ 4.25

Try It 2.98

ⓐ −6 < x < 2 −6 < x < 2 ⓑ −3 ≤ x < −1 −3 ≤ x < −1 ⓒ 2.5 ≤ x ≤ 6 2.5 ≤ x ≤ 6

Solve Linear Inequalities

A linear inequality is much like a linear equation—but the equal sign is replaced with an inequality sign. A linear inequality is an inequality in one variable that can be written in one of the forms, a x + b < c , a x + b < c , a x + b ≤ c , a x + b ≤ c , a x + b > c , a x + b > c , or a x + b ≥ c . a x + b ≥ c .

Linear Inequality

A linear inequality is an inequality in one variable that can be written in one of the following forms where a , b , and c are real numbers and a ≠ 0 a ≠ 0 :

When we solved linear equations, we were able to use the properties of equality to add, subtract, multiply, or divide both sides and still keep the equality. Similar properties hold true for inequalities.

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality. For example:

Notice that the inequality sign stayed the same.

This leads us to the Addition and Subtraction Properties of Inequality.

Addition and Subtraction Property of Inequality

For any numbers a , b , and c, if a < b , then a < b , then

For any numbers a , b , and c, if a > b , then a > b , then

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality.

What happens to an inequality when we divide or multiply both sides by a constant?

Let’s first multiply and divide both sides by a positive number.

The inequality signs stayed the same.

Does the inequality stay the same when we divide or multiply by a negative number?

Notice that when we filled in the inequality signs, the inequality signs reversed their direction.

When we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses.

This gives us the Multiplication and Division Property of Inequality.

Multiplication and Division Property of Inequality

For any numbers a , b , and c ,

When we divide or multiply an inequality by a :

• positive number, the inequality stays the same.
• negative number, the inequality reverses.

Sometimes when solving an inequality, as in the next example, the variable ends upon the right. We can rewrite the inequality in reverse to get the variable to the left.

Think about it as “If Xander is taller than Andy, then Andy is shorter than Xander.”

Example 2.50

Solve each inequality. Graph the solution on the number line, and write the solution in interval notation.

ⓐ x − 3 8 ≤ 3 4 x − 3 8 ≤ 3 4 ⓑ 9 y < ​ ​ 54 9 y < ​ ​ 54 ⓒ −15 < 3 5 z −15 < 3 5 z

Try It 2.99

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ p − 3 4 ≥ 1 6 p − 3 4 ≥ 1 6 ⓑ 9 c > 72 9 c > 72 ⓒ 24 ≤ 3 8 m 24 ≤ 3 8 m

Try It 2.100

ⓐ r − 1 3 ≤ 7 12 r − 1 3 ≤ 7 12 ⓑ 12 d ≤ ​ 60 12 d ≤ ​ 60 ⓒ −24 < 4 3 n −24 < 4 3 n

Be careful when you multiply or divide by a negative number—remember to reverse the inequality sign.

Example 2.51

Solve each inequality, graph the solution on the number line, and write the solution in interval notation.

ⓐ −13 m ≥ 65 −13 m ≥ 65 ⓑ n −2 ≥ 8 n −2 ≥ 8

Try It 2.101

ⓐ −8 q < 32 −8 q < 32 ⓑ k −12 ≤ 15 . k −12 ≤ 15 .

Try It 2.102

ⓐ −7 r ≤ ​ − 70 −7 r ≤ ​ − 70 ⓑ u −4 ≥ −16 . u −4 ≥ −16 .

Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but make sure to pay close attention when we multiply or divide to isolate the variable.

Example 2.52

Solve the inequality 6 y ≤ 11 y + 17 , 6 y ≤ 11 y + 17 , graph the solution on the number line, and write the solution in interval notation.

Try It 2.103

Solve the inequality, graph the solution on the number line, and write the solution in interval notation: 3 q ≥ 7 q − 23 . 3 q ≥ 7 q − 23 .

Try It 2.104

Solve the inequality, graph the solution on the number line, and write the solution in interval notation: 6 x < 10 x + 19 . 6 x < 10 x + 19 .

When solving inequalities, it is usually easiest to collect the variables on the side where the coefficient of the variable is largest. This eliminates negative coefficients and so we don’t have to multiply or divide by a negative—which means we don’t have to remember to reverse the inequality sign.

Example 2.53

Solve the inequality 8 p + 3 ( p − 12 ) > 7 p − 28 , 8 p + 3 ( p − 12 ) > 7 p − 28 , graph the solution on the number line, and write the solution in interval notation.

Try It 2.105

Solve the inequality 9 y + 2 ( y + 6 ) > 5 y − 24 9 y + 2 ( y + 6 ) > 5 y − 24 , graph the solution on the number line, and write the solution in interval notation.

Try It 2.106

Solve the inequality 6 u + 8 ( u − 1 ) > 10 u + 32 6 u + 8 ( u − 1 ) > 10 u + 32 , graph the solution on the number line, and write the solution in interval notation.

Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.

Example 2.54

Solve the inequality 8 x − 2 ( 5 − x ) < 4 ( x + 9 ) + 6 x , 8 x − 2 ( 5 − x ) < 4 ( x + 9 ) + 6 x , graph the solution on the number line, and write the solution in interval notation.

Try It 2.107

Solve the inequality 4 b − 3 ( 3 − b ) > 5 ( b − 6 ) + 2 b 4 b − 3 ( 3 − b ) > 5 ( b − 6 ) + 2 b , graph the solution on the number line, and write the solution in interval notation.

Try It 2.108

Solve the inequality 9 h − 7 ( 2 − h ) < 8 ( h + 11 ) + 8 h 9 h − 7 ( 2 − h ) < 8 ( h + 11 ) + 8 h , graph the solution on the number line, and write the solution in interval notation.

We can clear fractions in inequalities much as we did in equations. Again, be careful with the signs when multiplying or dividing by a negative.

Example 2.55

Solve the inequality 1 3 a − 1 8 a > 5 24 a ​ + 3 4 , 1 3 a − 1 8 a > 5 24 a ​ + 3 4 , graph the solution on the number line, and write the solution in interval notation.

Try It 2.109

Solve the inequality 1 4 x − 1 12 x > 1 6 x + 7 8 1 4 x − 1 12 x > 1 6 x + 7 8 , graph the solution on the number line, and write the solution in interval notation.

Try It 2.110

Solve the inequality 2 5 z − 1 3 z < 1 15 z ​ − 3 5 2 5 z − 1 3 z < 1 15 z ​ − 3 5 , graph the solution on the number line, and write the solution in interval notation.

Translate to an Inequality and Solve

To translate English sentences into inequalities, we need to recognize the phrases that indicate the inequality. Some words are easy, like “more than” and “less than.” But others are not as obvious. Table 2.2 shows some common phrases that indicate inequalities.

Example 2.56

Translate and solve. Then graph the solution on the number line, and write the solution in interval notation.

Try It 2.111

Nineteen less than p is no less than 47.

Try It 2.112

Four more than a is at most 15.

Solve Applications with Linear Inequalities

Many real-life situations require us to solve inequalities. The method we will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations.

We will read the problem and make sure all the words are understood. Next, we will identify what we are looking for and assign a variable to represent it. We will restate the problem in one sentence to make it easy to translate into an inequality. Then, we will solve the inequality.

Sometimes an application requires the solution to be a whole number, but the algebraic solution to the inequality is not a whole number. In that case, we must round the algebraic solution to a whole number. The context of the application will determine whether we round up or down.

Example 2.57

Dawn won a mini-grant of $4,000 to buy tablet computers for her classroom. The tablets she would like to buy cost $254.12 each, including tax and delivery. What is the maximum number of tablets Dawn can buy?

Try It 2.113

Angie has $20 to spend on juice boxes for her son’s preschool picnic. Each pack of juice boxes costs $2.63. What is the maximum number of packs she can buy?

Try It 2.114

Daniel wants to surprise his girlfriend with a birthday party at her favorite restaurant. It will cost $42.75 per person for dinner, including tip and tax. His budget for the party is $500. What is the maximum number of people Daniel can have at the party?

Example 2.58

Taleisha’s phone plan costs her $28.80 a month plus $0.20 per text message. How many text messages can she send/receive and keep her monthly phone bill no more than $50?

Try It 2.115

Sergio and Lizeth have a very tight vacation budget. They plan to rent a car from a company that charges $75 a week plus $0.25 a mile. How many miles can they travel during the week and still keep within their $200 budget?

Try It 2.116

Rameen’s heating bill is $5.42 per month plus $1.08 per therm. How many therms can Rameen use if he wants his heating bill to be a maximum of $87.50.

Profit is the money that remains when the costs have been subtracted from the revenue. In the next example, we will find the number of jobs a small businesswoman needs to do every month in order to make a certain amount of profit.

Example 2.59

Felicity has a calligraphy business. She charges $2.50 per wedding invitation. Her monthly expenses are $650. How many invitations must she write to earn a profit of at least $2,800 per month?

Try It 2.117

Caleb has a pet sitting business. He charges $32 per hour. His monthly expenses are $2,272. How many hours must he work in order to earn a profit of at least $800 per month?

Try It 2.118

Elliot has a landscape maintenance business. His monthly expenses are $1,100. If he charges $60 per job, how many jobs must he do to earn a profit of at least $4,000 a month?

There are many situations in which several quantities contribute to the total expense. We must make sure to account for all the individual expenses when we solve problems like this.

Example 2.60

Malik is planning a six-day summer vacation trip. He has $840 in savings, and he earns $45 per hour for tutoring. The trip will cost him $525 for airfare, $780 for food and sightseeing, and $95 per night for the hotel. How many hours must he tutor to have enough money to pay for the trip?

Try It 2.119

Brenda’s best friend is having a destination wedding and the event will last three days. Brenda has $500 in savings and can earn $15 an hour babysitting. She expects to pay $350 airfare, $375 for food and entertainment and $60 a night for her share of a hotel room. How many hours must she babysit to have enough money to pay for the trip?

Try It 2.120

Josue wants to go on a 10-night road trip with friends next spring. It will cost him $180 for gas, $450 for food, and $49 per night to share a motel room. He has $520 in savings and can earn $30 per driveway shoveling snow. How many driveways must he shovel to have enough money to pay for the trip?

Section 2.5 Exercises

Practice makes perfect.

In the following exercises, graph each inequality on the number line and write in interval notation.

ⓐ x < −2 x < −2 ⓑ x ≥ −3.5 x ≥ −3.5 ⓒ x ≤ 2 3 x ≤ 2 3

ⓐ x > 3 x > 3 ⓑ x ≤ −0.5 x ≤ −0.5 ⓒ x ≥ 1 3 x ≥ 1 3

ⓐ x ≥ −4 x ≥ −4 ⓑ x < 2.5 x < 2.5 ⓒ x > − 3 2 x > − 3 2

ⓐ x ≤ 5 x ≤ 5 ⓑ x ≥ −1.5 x ≥ −1.5 ⓒ x < − 7 3 x < − 7 3

ⓐ −5 < x < 2 −5 < x < 2 ⓑ −3 ≤ x < 1 −3 ≤ x < 1 ⓒ 0 ≤ x ≤ 1.5 0 ≤ x ≤ 1.5

ⓐ −2 < x < 0 −2 < x < 0 ⓑ −5 ≤ x < −3 −5 ≤ x < −3 ⓒ 0 ≤ x ≤ 3.5 0 ≤ x ≤ 3.5

ⓐ −1 < x < 3 −1 < x < 3 ⓑ −3 < x ≤ −2 −3 < x ≤ −2 ⓒ −1.25 ≤ x ≤ 0 −1.25 ≤ x ≤ 0

ⓐ −4 < x < 2 −4 < x < 2 ⓑ −5 < x ≤ −2 −5 < x ≤ −2 ⓒ −3.75 ≤ x ≤ 0 −3.75 ≤ x ≤ 0

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

ⓐ a + 3 4 ≥ 7 10 a + 3 4 ≥ 7 10 ⓑ 8 x > 72 8 x > 72 ⓒ 20 > 2 5 h 20 > 2 5 h

ⓐ b + 7 8 ≥ 1 6 b + 7 8 ≥ 1 6 ⓑ 6 y < 48 6 y < 48 ⓒ 40 < 5 8 k 40 < 5 8 k

ⓐ f − 13 20 < − 5 12 f − 13 20 < − 5 12 ⓑ 9 t ≥ −27 9 t ≥ −27 ⓒ 7 6 j ≥ 42 7 6 j ≥ 42

ⓐ g − 11 12 < − 5 18 g − 11 12 < − 5 18 ⓑ 7 s < −28 7 s < −28 ⓒ 9 4 g ≤ 36 9 4 g ≤ 36

ⓐ −5 u ≥ 65 −5 u ≥ 65 ⓑ a −3 ≤ 9 a −3 ≤ 9

ⓐ −8 v ≤ 96 −8 v ≤ 96 ⓑ b −10 ≥ 30 b −10 ≥ 30

ⓐ −9 c < 126 −9 c < 126 ⓑ −25 < p −5 −25 < p −5

ⓐ −7 d > 105 −7 d > 105 ⓑ −18 > q −6 −18 > q −6

4 v ≥ 9 v − 40 4 v ≥ 9 v − 40

5 u ≤ 8 u − 21 5 u ≤ 8 u − 21

13 q < 7 q − 29 13 q < 7 q − 29

9 p > 14 p − 18 9 p > 14 p − 18

12 x + 3 ( x + 7 ) > 10 x − 24 12 x + 3 ( x + 7 ) > 10 x − 24

9 y + 5 ( y + 3 ) < 4 y − 35 9 y + 5 ( y + 3 ) < 4 y − 35

6 h − 4 ( h − 1 ) ≤ 7 h − 11 6 h − 4 ( h − 1 ) ≤ 7 h − 11

4 k − ( k − 2 ) ≥ 7 k − 26 4 k − ( k − 2 ) ≥ 7 k − 26

8 m − 2 ( 14 − m ) ≥ ​ 7 ( m − 4 ) + 3 m 8 m − 2 ( 14 − m ) ≥ ​ 7 ( m − 4 ) + 3 m

6 n − 12 ( 3 − n ) ≤ 9 ( n − 4 ) + 9 n 6 n − 12 ( 3 − n ) ≤ 9 ( n − 4 ) + 9 n

3 4 b − 1 3 b < 5 12 b − 1 2 3 4 b − 1 3 b < 5 12 b − 1 2

9 u + 5 ( 2 u − 5 ) ≥ 12 ( u − 1 ) + 7 u 9 u + 5 ( 2 u − 5 ) ≥ 12 ( u − 1 ) + 7 u

2 3 g − 1 2 ( g − 14 ) ≤ 1 6 ( g + 42 ) 2 3 g − 1 2 ( g − 14 ) ≤ 1 6 ( g + 42 )

4 5 h − 2 3 ( h − 9 ) ≥ 1 15 ( 2 h + 90 ) 4 5 h − 2 3 ( h − 9 ) ≥ 1 15 ( 2 h + 90 )

5 6 a − 1 4 a > 7 12 a + 2 3 5 6 a − 1 4 a > 7 12 a + 2 3

12 v + 3 ( 4 v − 1 ) ≤ 19 ( v − 2 ) + 5 v 12 v + 3 ( 4 v − 1 ) ≤ 19 ( v − 2 ) + 5 v

15 k ≤ −40 15 k ≤ −40

35 k ≥ −77 35 k ≥ −77

23 p − 2 ( 6 − 5 p ) > 3 ( 11 p − 4 ) 23 p − 2 ( 6 − 5 p ) > 3 ( 11 p − 4 )

18 q − 4 ( 10 − 3 q ) < 5 ( 6 q − 8 ) 18 q − 4 ( 10 − 3 q ) < 5 ( 6 q − 8 )

− 9 4 x ≥ − 5 12 − 9 4 x ≥ − 5 12

− 21 8 y ≤ − 15 28 − 21 8 y ≤ − 15 28

c + 34 < −99 c + 34 < −99

d + 29 > −61 d + 29 > −61

m 18 ≥ −4 m 18 ≥ −4

n 13 ≤ −6 n 13 ≤ −6

In the following exercises, translate and solve. Then graph the solution on the number line and write the solution in interval notation.

Three more than h is no less than 25.

Six more than k exceeds 25.

Ten less than w is at least 39.

Twelve less than x is no less than 21.

Negative five times r is no more than 95.

Negative two times s is lower than 56.

Nineteen less than b is at most −22 . −22 .

Fifteen less than a is at least −7 . −7 .

In the following exercises, solve.

Alan is loading a pallet with boxes that each weighs 45 pounds. The pallet can safely support no more than 900 pounds. How many boxes can he safely load onto the pallet?

The elevator in Yehire’s apartment building has a sign that says the maximum weight is 2100 pounds. If the average weight of one person is 150 pounds, how many people can safely ride the elevator?

Andre is looking at apartments with three of his friends. They want the monthly rent to be no more than $2,360. If the roommates split the rent evenly among the four of them, what is the maximum rent each will pay?

Arleen got a $20 gift card for the coffee shop. Her favorite iced drink costs $3.79. What is the maximum number of drinks she can buy with the gift card?

Teegan likes to play golf. He has budgeted $60 next month for the driving range. It costs him $10.55 for a bucket of balls each time he goes. What is the maximum number of times he can go to the driving range next month?

Ryan charges his neighbors $17.50 to wash their car. How many cars must he wash next summer if his goal is to earn at least $1,500?

Keshad gets paid $2,400 per month plus 6% of his sales. His brother earns $3,300 per month. For what amount of total sales will Keshad’s monthly pay be higher than his brother’s monthly pay?

Kimuyen needs to earn $4,150 per month in order to pay all her expenses. Her job pays her $3,475 per month plus 4% of her total sales. What is the minimum Kimuyen’s total sales must be in order for her to pay all her expenses?

Andre has been offered an entry-level job. The company offered him $48,000 per year plus 3.5% of his total sales. Andre knows that the average pay for this job is $62,000. What would Andre’s total sales need to be for his pay to be at least as high as the average pay for this job?

Nataly is considering two job offers. The first job would pay her $83,000 per year. The second would pay her $66,500 plus 15% of her total sales. What would her total sales need to be for her salary on the second offer be higher than the first?

Jake’s water bill is $24.80 per month plus $2.20 per ccf (hundred cubic feet) of water. What is the maximum number of ccf Jake can use if he wants his bill to be no more than $60?

Kiyoshi’s phone plan costs $17.50 per month plus $0.15 per text message. What is the maximum number of text messages Kiyoshi can use so the phone bill is no more than $56.60?

Marlon’s TV plan costs $49.99 per month plus $5.49 per first-run movie. How many first-run movies can he watch if he wants to keep his monthly bill to be a maximum of $100?

Kellen wants to rent a banquet room in a restaurant for her cousin’s baby shower. The restaurant charges $350 for the banquet room plus $32.50 per person for lunch. How many people can Kellen have at the shower if she wants the maximum cost to be $1,500?

Moshde runs a hairstyling business from her house. She charges $45 for a haircut and style. Her monthly expenses are $960. She wants to be able to put at least $1,200 per month into her savings account order to open her own salon. How many “cut & styles” must she do to save at least $1,200 per month?

Noe installs and configures software on home computers. He charges $125 per job. His monthly expenses are $1,600. How many jobs must he work in order to make a profit of at least $2,400?

Katherine is a personal chef. She charges $115 per four-person meal. Her monthly expenses are $3,150. How many four-person meals must she sell in order to make a profit of at least $1,900?

Melissa makes necklaces and sells them online. She charges $88 per necklace. Her monthly expenses are $3,745. How many necklaces must she sell if she wants to make a profit of at least $1,650?

Five student government officers want to go to the state convention. It will cost them $110 for registration, $375 for transportation and food, and $42 per person for the hotel. There is $450 budgeted for the convention in the student government savings account. They can earn the rest of the money they need by having a car wash. If they charge $5 per car, how many cars must they wash in order to have enough money to pay for the trip?

Cesar is planning a four-day trip to visit his friend at a college in another state. It will cost him $198 for airfare, $56 for local transportation, and $45 per day for food. He has $189 in savings and can earn $35 for each lawn he mows. How many lawns must he mow to have enough money to pay for the trip?

Alonzo works as a car detailer. He charges $175 per car. He is planning to move out of his parents’ house and rent his first apartment. He will need to pay $120 for application fees, $950 for security deposit, and first and last months’ rent at $1,140 per month. He has $1,810 in savings. How many cars must he detail to have enough money to rent the apartment?

Eun-Kyung works as a tutor and earns $60 per hour. She has $792 in savings. She is planning an anniversary party for her parents. She would like to invite 40 guests. The party will cost her $1,520 for food and drinks and $150 for the photographer. She will also have a favor for each of the guests, and each favor will cost $7.50. How many hours must she tutor to have enough money for the party?

Everyday Math

Maximum load on a stage In 2014, a high school stage collapsed in Fullerton, California, when 250 students got on stage for the finale of a musical production. Two dozen students were injured. The stage could support a maximum of 12,750 pounds. If the average weight of a student is assumed to be 140 pounds, what is the maximum number of students who could safely be on the stage?

Maximum weight on a boat In 2004, a water taxi sank in Baltimore harbor and five people drowned. The water taxi had a maximum capacity of 3,500 pounds (25 people with average weight 140 pounds). The average weight of the 25 people on the water taxi when it sank was 168 pounds per person. What should the maximum number of people of this weight have been?

Wedding budget Adele and Walter found the perfect venue for their wedding reception. The cost is $9850 for up to 100 guests, plus $38 for each additional guest. How many guests can attend if Adele and Walter want the total cost to be no more than $12,500?

Shower budget Penny is planning a baby shower for her daughter-in-law. The restaurant charges $950 for up to 25 guests, plus $31.95 for each additional guest. How many guests can attend if Penny wants the total cost to be no more than $1,500?

Writing Exercises

Explain why it is necessary to reverse the inequality when solving −5 x > 10 . −5 x > 10 .

Explain why it is necessary to reverse the inequality when solving n −3 < 12 . n −3 < 12 .

Find your last month’s phone bill and the hourly salary you are paid at your job. Calculate the number of hours of work it would take you to earn at least enough money to pay your phone bill by writing an appropriate inequality and then solving it. Do you feel this is an appropriate number of hours? Is this the appropriate phone plan for you?

Find out how many units you have left, after this term, to achieve your college goal and estimate the number of units you can take each term in college. Calculate the number of terms it will take you to achieve your college goal by writing an appropriate inequality and then solving it. Is this an acceptable number of terms until you meet your goal? What are some ways you could accelerate this process?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/2-5-solve-linear-inequalities

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 4: Linear Equations and Inequalities in One Variable

4.2.2 solving linear inequalities, learning outcomes.

• Solve single-step linear inequalities
• Solve multi-step linear inequalities
• Write a solution set in interval notation
• Write solution set in set-builder notation
• Solution set : a set containing the solutions

Properties of Inequality

A linear inequality is similar to a linear equation in many ways, but do the properties of equality still hold? An inequality like [latex]2\lt 5[/latex] can be visualized as an unbalanced scale:

It seems logical that adding or subtracting the same amount from both sides of the scale will not change the imbalance.

Consider the simple inequality [latex]2 \lt 5[/latex]. Let’s add [latex]4[/latex] to each side and determine if the inequality still holds:

[latex]\begin{equation}\begin{aligned}2 & \lt\ 5 \\ 2 \color{blue}{+4} & \lt 5\color{blue}{+4} \\ 6 & \lt 9 \end{aligned}\end{equation}[/latex]

Adding the same number to both sides keeps the inequality in tact. Let’s try subtracting [latex]3[/latex] from both sides to see what happens:

[latex]\begin{equation}\begin{aligned}2 & \lt\ 5 \\ 2 \color{blue}{-3} & \lt 5\color{blue}{-3} \\ -1 & \lt 2 \end{aligned}\end{equation}[/latex]

Subtracting the same number to both sides keeps the inequality in tact.

The addition and subtraction property of equality applies to inequalities. But what of the multiplication and division properties of equality? Let’s consider the inequality [latex]2\lt 5[/latex] again, and start by multiplying both sides by a positive number.

[latex]\begin{equation}\begin{aligned}2 & \lt\ 5 \\ 2 \color{blue}{\cdot 3} & \lt 5\color{blue}{\cdot 3} \\ 6 & \lt 15 \end{aligned}\end{equation}[/latex]

The inequality still holds. But what about multiplying by a negative number?

[latex]\begin{equation}\begin{aligned}2 & \lt\ 5 \\ 2 \color{blue}{\cdot (-4)} & \lt 5\color{blue}{\cdot (-4)} \\ -8 & \lt -20 \end{aligned}\end{equation}[/latex]

Thuis results in a false statement! To make the statement true, we must flip the [latex]\lt[/latex] sign to a [latex]\gt[/latex] sign because [latex]-8\gt -20[/latex]. The same thing happens if we try to divide by a negative number: we must flip the inequality sign.

Properties of inequality

For all real numbers [latex]a,\,b,\,c[/latex], if [latex]a<b[/latex] then [latex]a+c\lt b+c[/latex].

Adding or subtracting the same term to both sides an inequality keeps the inequality true.

For all real numbers [latex]a,\,b,\,c[/latex] with [latex]c\gt 0[/latex], if [latex]a<b[/latex] then [latex]a\cdot c\lt b\cdot c[/latex].

Multiplying or dividing by a positive term to both sides an inequality keeps the inequality true.

For all real numbers [latex]a,\,b,\,c[/latex] with [latex]c\lt 0[/latex], if [latex]a\lt b[/latex] then [latex]a\cdot c\gt b\cdot c[/latex].

To multiply or divide by a negative term  on both sides of an inequality we must reverse the inequality sign.

Solving an linear inequality follows the same rules as solving a linear equation. In the first example, we use the multiplication and division property to isolate the variable.

1. [latex]3x\lt 6[/latex]   Write your answer in set-builder notation.

2. [latex]-2x - 1\ge 5[/latex]   Write your answer in interval notation.

3. [latex]5-x\geq 10[/latex]   Graph your answer on a number line.

1. [latex]\begin{equation}\begin{aligned} 3x & < 6 \\ \color{blue}{\frac{1}{3}}\left( 3x \right) & < \left ( 6\right )\color{blue}{\frac{1}{3}}\;\;\;\;\;\;\;\;\;\;\text{Multiply both sides by }\frac{1}{3} \text{ (or divide both sides by }3) \\ x & \lt 2 \end{aligned}\end{equation}[/latex]

Answer: [latex]\{\;x\;\large |\normalsize\;\;x \lt 2,\;x\in\mathbb{R}\;\}[/latex]

2. [latex]\begin{equation}\begin{aligned}-2x - 1 & \ge 5\;\;\;\;\;\;\;\;\;\;\text{Add 1 to both sides} \\ -2x & \ge 6\\ \color{blue}{\left(-\frac{1}{2}\right)}\left(-2x\right) & \color{blue}{\le} \left(6\right)\color{blue}{\left(-\frac{1}{2}\right)}\;\;\;\;\;\;\;\;\;\;\text{Multiply both sides by }-\frac{1}{2} \text{ and reverse the inequality sign} \\ x & \le -3\end{aligned}\end{equation}[/latex]

Answer: [latex]x\in \left ( -\infty,\,-3\right ][/latex]

3. [latex]\begin{equation}\begin{aligned}5-x & \geq10 \\ -x & \geq 5\\ \color{blue}{\left(-1\right)}\left(-x\right) & \color{blue}{\leq} \left(5\right)\color{blue}{\left(-1\right)}\;\;\;\;\;\;\;\;\;\;\text{Multiply both sides by } -1\text{ and reverse the sign}\\ x & \leq-5\end{aligned}\end{equation}[/latex]

1. [latex]4x\ge -8[/latex]   Write your answer in set-builder notation.

2. [latex]-5x\gt 4[/latex]   Write your answer in interval notation.

3. [latex]-3x\lt -9[/latex] Graph your answer on a number line.

• [latex]\{\;x\;\large |\normalsize\;\;x \ge 2,\;x\in\mathbb{R}\;\}[/latex]
• [latex]x\in\left (-\infty,\,-\frac{4}{5}\right )[/latex]

In our next example, we will use the addition property to solve inequalities.

Solve. Write the answer in interval notation.

1. [latex]x - 15\lt 4[/latex]

2. [latex]6\ge x - 1[/latex]

3. [latex]x+7\gt 9[/latex]

1. [latex]\begin{equation}\begin{aligned} x - 15 & \lt 4 \\ x - 15 \color{blue}{+15} & \lt 4 \color{blue}{+15}\;\;\;\;\;\;\;\;\;\; \text{Add 15 to both sides.}\\ x & \lt 19 \end{aligned}\end{equation}[/latex]

Answer: [latex]x\in\left ( -\infty,\,19\right )[/latex]

2. [latex]\begin{equation}\begin{aligned}6 & \geq x - 1 \\ 6\color{blue}{+1} & \geq x - 1 \color{blue}{+1} \;\;\;\;\;\;\;\;\;\; \text{Add 1 to both sides}. \\ 7 & \geq x \end{aligned}\end{equation}[/latex]

Answer: [latex]x\in\left ( -\infty,\,7\right ][/latex]

3. [latex]\begin{equation}\begin{aligned}x+7 & \gt 9\\ x+7 \color{blue}{- 7} & \gt 9\color{blue}{- 7}\;\;\;\;\;\;\;\;\;\; \text{Subtract 7 from both sides}.\\x & \gt 2\end{aligned}\end{equation}[/latex]

Answer: [latex]x\in\left [ 2,\,\infty\right )[/latex]

1. [latex]x-8\lt -6[/latex]

2. [latex]x+7\gt 7[/latex]

3. [latex]x+\frac{2}{5}\geq -\frac{2}{5}[/latex]

• [latex]x\in\left (-\infty,\,2\right )[/latex]
• [latex]x\in\left (0,\,\infty\right )[/latex]
• [latex]x\in\left [-\frac{4}{5},\,\infty\right )[/latex]

The following video shows examples of solving single-step inequalities using the multiplication and addition properties.

The following video shows examples of solving inequalities with the variable on the right side.

Solving Multi-Step Inequalities

As the previous examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations. We just have to remember to reverse the sign if we multiply or divide by a negative term . To isolate the variable and solve, we combine like terms and perform operations with the multiplication and addition properties.

Solve the inequality: [latex]13 - 7x\ge 10x - 4[/latex]. Write the solution in interval notation.

Solving this inequality is similar to solving an equation up until the last step.

The solution set is given by the interval [latex]\left(-\infty ,1\right][/latex].

In the next example, we solve an inequality that contains fractions. Notice how we need to reverse the inequality sign at the end because we multiply by a negative.

Solve the following inequality and write the answer in interval notation: [latex]-\frac{3}{4} x\ge -\frac{5}{8} +\frac{2}{3} x[/latex].

Instead of working with the fractions in this last example, we could clear the fractions by multiplying both sides by a common denominator.

The least common multiple of 4, 8 and 3 is 24. We will multiply both sides of the inequality by 24. This requires applying the distributive property to the two terms on the right side of the inequality.

Solve the following inequality and write the answer in interval notation: [latex]\frac{1}{3} x\le -\frac{4}{5} +\frac{3}{4} x[/latex].

[latex]x\in\left [\frac{48}{25},\,\infty\right )[/latex]

• Revision and Adaptation. Provided by: Lumen Learning. . Provided by : Lumen Learning. License : CC BY: Attribution
• Properties of Inequality; Clearing Fractions Example and Try It. Authored by : Hazel McKenna. Provided by : Utah Valley University. License : CC BY: Attribution
• Unit 10: Solving Equations and Inequalities, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution
• Ex. Solving One Step Inequalities by Adding and Subtracting (Variable Left Side). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/1Z22Xh66VFM . License : CC BY: Attribution
• Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Right Side). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/RBonYKvTCLU . License : CC BY: Attribution
• Ex: Solve One Step Linear Inequality by Dividing (Variable Left). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/IajiD3R7U-0 . License : CC BY: Attribution
• Ex: Solve One Step Linear Inequality by Dividing (Variable Right). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/s9fJOnVTHhs . License : CC BY: Attribution

Privacy Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.5: Quadratic inequalities

• Last updated
• Save as PDF
• Page ID 45114

• Darlene Diaz
• Santiago Canyon College via ASCCC Open Educational Resources Initiative

We can think about an earlier chapter where we obtained solutions for linear inequalities where the solutions are intervals of numbers. With quadratic inequalities, it is similar to linear inequalities, but, now, instead of lines, we have parabolas. Hence, we have two methods for solving quadratic inequalities: graphing or algebraically.

Solving Quadratic Inequalities by Graphing

We can use the zeros (or roots) of a graph of a quadratic equation to solve for quadratic inequalities. Recall, the zeros (or roots) of a graph are the \(x\)-intercepts, i.e., \(y = 0\).

Example 11.5.1

Solve \(x^2 − 3x − 4\geq 0\) by using the graphing method.

We first begin by graphing \(x^2 − 3x − 4\) as we would in the previous section. Recall, the \(x\)-coordinate of the vertex is \(−\dfrac{b}{2a}\). Hence,

\[-\dfrac{b}{2a}=-\dfrac{-3}{2(1)}=\dfrac{3}{2}=1.5\nonumber\]

The \(y\)-coordinate of the vertex is \(x^2 − 3x − 4\) evaluated for \(x = 1.5\):

\[(1.5)^2-3(1.5)-4=-6.25\nonumber\]

The vertex is at \((1.5, −6.25)\). The \(y\)-intercept is when \(x = 0\):

\[0^2-3(0)-4=-4\nonumber\]

and the \(x\)-intercepts are when \(x^2 − 3x − 4 = 0\). Solving for the roots we get

\[\begin{aligned}x^2-3x-4&=0 \\ (x-4)(x+1)&=0 \\ x-4=0\quad&\text{or}\quad x+1=0 \\ x=4\quad&\text{or}\quad x=-1\end{aligned}\]

Thus, the intercepts are \((0, −4),\: (4, 0),\) and \((−1, 0)\) with a vertex at \((1.5, −6.25)\). Now we draw the graph:

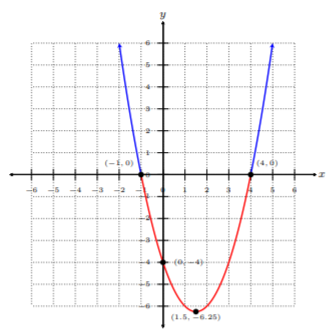
Given \(x^2 − 3x − 4\geq 0\) says we are specifically looking for the values of \(x^2 − 3x − 4\) in which are greater than or equal to zero. In other words, we are looking for all \(y\)-values that are above the \(x\)-axis because that is where all the \(y\)-values are positive. Looking at the graph above, these are all the values on the blue parts of the graph. Thus, using the graphing method, the solution is \((−∞, −1] ∪ [4, ∞)\). Note, we use brackets since it is \(\geq\).

Notice, we ignore the red part of the parabola since this is where \(x^2 − 3x − 4\) is negative, i.e., all the \(y\)-values are negative, because we were only looking for when \(x^2 − 3x − 4\geq 0\), the parts of the graph above the \(x\)-axis.

Solving Quadratic Inequalities Algebraically

The next method to solving quadratic inequalities is algebraically. Hence, there is a little more work involved since the method is algebraic. We must follow an order of steps to obtain the correct solution. The good news is that these two methods are similar where we always use the \(x\)-intercepts to determine the intervals.

Steps to solving quadratic inequalities

Step 1. Rewrite the inequality so that \(ax^2 + bx + c\) is on one side and zero is on the other.

Step 2. Determine where the inequality is zero using any method appropriate.

Step 3. Use the \(x\)-values obtained in the previous step to label on a number line.

Step 4. Take test values to observe where the inequality is true.

• If the inequality is \(< 0\) or \(\leq 0\), then the inequality is true where the test values are negative.
• If the inequality is \(> 0\) or \(\geq 0\), then the inequality is true where the test values are positive.

Step 5. Write the solution in interval notation.

Example 11.5.2

Solve algebraically: \(-x^2+8>2x\)

Step 1. We rewrite \(−x^2 + 8 > 2x\) so that zero is on one side: \[-x^2-2x+8>0\nonumber\]

Step 2. We set the left side equal to zero to obtain the roots (or zeros): \[\begin{aligned} -x^2-2x+8&=0 \\ x^2+2x-8&=0 \\ (x+4)(x-2)&=0 \\ x+4=0\quad&\text{or}\quad x-2=0 \\ x=-4\quad&\text{or}\quad x=2\end{aligned}\]

Step 3. Label \(-4\) and \(2\) on a blank number line:

Step 4. We take test values on each side of \(−4\) and \(2\). Let’s choose fairly easy numbers such as \(−5,\: 0\), and \(3\). We plug these numbers into \(−x^2 − 2x + 8\) and determine whether the value is positive or negative:

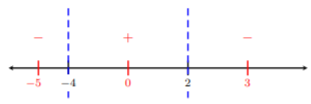
\[\begin{aligned} -(-5)^2-2(-5)+8&=-7<0\quad\Longrightarrow\quad\text{letting }x=-5 \\ -(0)^2-2(0)+8&=8>0\quad\Longrightarrow\quad\text{letting }x=0 \\ -(3)^2-2(3)+8&=-7<0\quad\Longrightarrow\quad\text{letting }x=3\end{aligned}\]

Step 5. Since \(−x^2 − 2x + 8 > 0\) (from Step 1. ), then we are looking for where the test values are positive. Looking at the number line above, we see these are the values in between \(−4\) and \(2\). Thus, the solution is \((−4, 2)\). Note, we use parenthesis since the inequality symbol is \(>\).

Quadratic Inequalities Homework

Solve the inequality. Write the solution in interval notation.

Exercise 11.5.1

\(x^2-9x+18>0\)

Exercise 11.5.2

\(x^2-2x-24\leq 0\)

Exercise 11.5.3

\(x^2-2x-3<0\)

Exercise 11.5.4

\(x^2+10x+24\geq 0\)

Exercise 11.5.5

\(x^2-4x+4>0\)

Exercise 11.5.6

\(x^2+2x\geq 8\)

Exercise 11.5.7

\(x^2-4x\leq -3\)

Exercise 11.5.8

\(3x^2+7x-20\leq 0\)

Exercise 11.5.9

\(4x^2+11x-20\geq 0\)

Exercise 11.5.10

\(3x^2+2x-1<0\)

Exercise 11.5.11

\(-4x^2+7x\geq 0\)

Exercise 11.5.12

\(x^2+6x\geq 0\)

Exercise 11.5.13

\(x^2-12x+36<0\)

Exercise 11.5.14

\(x^2-2x+1\geq 0\)